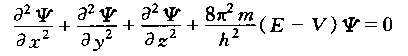2-1.微观粒子与量子力学:电子及电子以下(中子,质子,离子,分子是实物粒子)都可认为是微观粒子。化学反应中,原子核没有发生变化,只是核外电子的运动状态发生变化。
电子属微观粒子,微观粒子的运动规律与经典的宏观运动规律不完全一致。因此,用宏观运动的牛顿定律就无法描述许多微观粒子的运动现象,而只能用量子力学理论来描述。
当电子由一个定态轨道跃迁到另一个定态轨道时,由于两个定态轨道的能级不同,会吸收或放出一定的能量。若这种能量以光的形式表现,光的能量hν等子这两个定态轨道的能量级差:hν=E2-E1,能量差值(E2-E1)不可能是无穷小,即电子轨道的能级E1、E2…是不连续的,这个电子轨道能量级的特征称为轨道能量量子化。
能级跃迁
2-2.微观粒子的特征:微观粒子的运动具有波粒二象性。通过光在传播过程中的干涉、衍射等现象,人们认识光的波动性;而通过光和物质相互作用时的光电效应现象,人们认识光的微粒性,这就是所谓的光的波粒二象性。
表征光的粒子性的动量P与表征光的波动性的波长λ之间的关系是:λ =h/P = h/mυ。物质波指物质在空间中某点某时刻可能出现的几率,一切微观粒子,包括电子和质子、中子,都有波粒二象性。
电子衍射
2-3 薛定谔方程和波函数:薛定谔根据微观粒子的波粒二象性的理论和测不准原理,建立了微观粒子的波动方程,为薛定谔方程,是一个二阶偏微分方程:
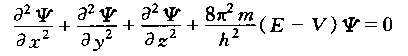
式中,Ψ是波函数;x、y、z是三维空间坐标;E是体系的总能量;V是体系的势能;m是微观粒子的质量,h是普朗克常数。
薛定谔方程将电子在核外运动的位置(由x、y、z决定)与能量E联系起来,即薛定谔方程将微观粒子的粒子性(m、E)与波动性Ψ(x、y、z)统一起来,从而能更全面地反映微观粒子的运动状态。核外电子在原子轨道中某体积域内出现的几率,这种〝几率图〞又叫电子云。
2-4 原子中电子的四量子数:波函数Ψ中,将r、θ、φ更换成n、l、m丝毫不影响波函数Ψ的性质,但对于解释核外电子的运动却更清晰、明确。n、l、m不是连续量,而是量子化的量,即必须是整数。n、l、m值确定时,波函数Ψ也就确定了,n、l、m称为〝原子轨道〞的量子数。
n是主量子数,取值范围从l到任何一个正整数,其中每一个n值代表一个电子轨道层,又称作〝原子轨道〞。
l称为副量子数或角量子数,从核外电子的分布状况看,规定l的取值范围为从0到(n-l)的正整数,共可取n个值。其中每一个l值代表一个原子轨道亚层。
m称为磁量子数,它表达了原子轨道的伸展方向,实际上它反映了波函数Ψ(r、θ、φ)在空间定义域的个数。规定取值范围为从-1到+l的整数,共(2l+1)个取值,各对应于不同的伸展方向。从m的取值范围的规定可知|m|≤l。
要描述一个电子在轨道上所具有的能量还要增加第四个量子数即自旋量子数ms。因为电子除了围绕原子核公转外,它还要围绕自已的轴自转。自转的方向只能有有顺时针和逆时针二种,表征电子自旋方向的自旋量子数ms也只有二个:+1/2和-1/2。
电子自旋