1-1.数据：数据就是数值，也就是我们通过观察、实验或计算得出的结果。数据有三大特征，一是源头来自于测量，二是一般带有单位，第三也是最重要的是，数据必然有误差存在。而数学中的数，则无需测量，没有单位，也没有误差。数据和数遵循的运算规则是一致的，所以在以前的学习中，我们往往模糊了数据和数的差别。而在分析化学中，接触到的数实际上有很多是数据，在处理时需要有额外的注意事项。
1-2.误差：测定值与真值之间的差值，即(Xi－X)称为误差，或绝对误差，还有相对误差，即(Xi－X)/X。误差值>0，称为正误差，误差值<0，称为负误差。误差的来源可以分为系统误差和随机误差（偶然误差）。由于操作者马虎犯错造成的实验误差，叫做过失误差，本质上也可以看成是系统误差的一种。误差反映了实验的准确度，误差越小，代表实验数据越准确。
1-3.随机误差的正态分布曲线：随机误差的显著特点是无法预测其误差大小和方向，但是在大量测量中随机误差的出现还是有其规律的，即服从正态分布。正态分布曲线是以测量值的数轴为横坐标，以测量值出现的频率为纵坐标绘制的曲线，特点是以真值为中心左右对称，且离真值越近曲线纵坐标值越大，说明：（1）随机误差出现正误差和负误差的概率相等；（2）随机误差大误差概率小，小误差概率大。因此虽然随机误差是无法校正和克服的，但是可以通过多次测量求平均值的做法来减免。
1-4 偏差：测量值与平均值之差称为偏差，d = Xi－X。由于测量值往往是多次的，所以一般用多次测量值与平均值差值的平均值来表示，即平均偏差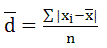
。注意，平均偏差值是大于零的，这样算出来的平均偏差属于绝对偏差，还有相对平均偏差，即
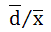。此外，实验中还往往需要计算数据的标准偏差，即
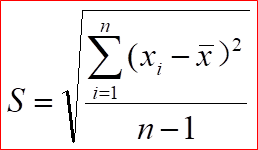，还有相对标准偏差，也称变异系数
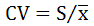。偏差代表的是数据的集中程度，也就是精密度，偏差越小，代表数据越精密。标准偏差能够放大大偏差的权重，所以比平均偏差更有统计学上的意义。
1-5.置信区间与置信度：在只考虑随机误差的情况下，平均值虽然不是真值，但离真值也不会太远。根据统计规律，可以找到一定概率下，真值的可能落在的区间范围是：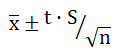
，式中S即为测量的标准偏差，n为测量次数，t是需要查表的数值。我们把这个区间范围称为置信区间，而对应真值落在其中的概率称为置信度。在其他情况不变的条件下，置信度越高，对应的置信区间范围越大；在一定的置信度下，测量的次数越多，或者测量的标准偏差越小，则对应的置信区间范围越窄。
