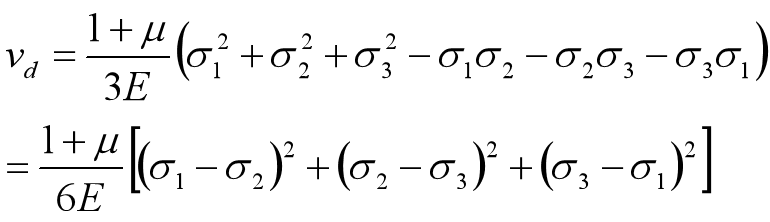暂无搜索结果
-
1 绪论
-
1.1 学习任务单(含学习目标)
-
1.2 材料力学的任务
-
1.3 变形固体的基本假设
-
1.4 外力及其分类
-
1.5 内力、截面法和应力
-
1.6 变形与应变
-
1.7 构件分类及杆件变形的基本形式
-
1.8 章节测验
-
1.9 计算题1-1 截面内力
-
2 拉压与剪切
-
2.1 学习任务单(含学习目标)
-
2.2 轴向拉压的内力
-
2.3 轴向拉压的应力
-
2.4 习题2-1 内力与应力
-
2.5 习题2-2 斜截面应力
-
2.6 轴向拉压的变形
-
2.7 习题2-3 变形
-
2.8 材料拉压的力学性能
-
2.9 章节测验1
-
2.10 轴向拉压的强度条件
-
2.11 习题2-4 强度条件
-
2.12 轴向拉伸或压缩时的应变能
-
2.13 拉压超静定问题
-
2.14 习题2-5 超静定
-
2.15 温度应力和装配应力
-
2.16 习题2-6 温度应力
-
2.17 应力集中
-
2.18 剪切和挤压
-
2.19 习题2-7 剪切和挤压
-
2.20 章节测验2
-
2.21 第2章 课件
-
3 扭转
-
3.1 学习任务单(含学习目标)
-
3.2 扭转的概念 外力偶矩 扭矩和扭矩图
-
3.3 纯剪切
-
3.4 章节测验1
-
3.5 圆轴扭转的应力和变形
-
3.6 扭转强度条件和刚度条件
-
3.7 章节测验2
-
3.8 习题3-1 内力
-
3.9 习题3-2 应力
-
3.10 习题3-3 强度和刚度
-
3.11 第3章 课件
-
4 弯曲内力
-
4.1 学习任务单(含学习目标)
-
4.2 弯曲的基本概念
-
4.3 剪力和弯矩 剪力图和弯矩图
-
4.4 剪力、弯矩与载荷集度的关系
-
4.5 按叠加原理做弯矩图
-
4.6 平面刚架和曲杆的内力
-
4.7 章节测验
-
4.8 第4章 弯曲内力
-
5 弯曲应力
-
5.1 学习任务单(含学习目标)
-
5.2 纯弯曲和横力弯曲的概念
-
5.3 纯弯曲时的正应力
-
5.4 横力弯曲时的正应力
-
5.5 弯曲切应力
-
5.6 提高弯曲强度的措施
-
5.7 章节测验
-
5.8 第5章 弯曲应力 课件
-
6 弯曲变形
-
6.1 学习任务单(含学习目标)
-
6.2 工程中的弯曲变形问题
-
6.3 挠曲线的微分方程
-
6.4 用积分法求弯曲变形
-
6.5 用叠加法求弯曲变形 梁的刚度条件
-
6.6 简单超静定梁
-
6.7 提高弯曲刚度的措施
-
6.8 章节测验
-
6.9 第6章 弯曲变形 课件
-
7 应力状态 强度理论
-
7.1 学习任务单(含学习目标)
-
7.2 应力状态的概念
-
7.3 二向和三向应力状态的实例
-
7.4 二向应力状态分析的解析法
-
7.5 章节测验1
-
7.6 二向应力状态分析的图解法
-
7.7 三向应力状态
-
7.8 广义胡克定律
-
7.9 复杂应力状态的应变能密度
-
7.10 强度理论及其应用
-
7.11 章节测验
-
7.12 第7章 应力状态与强度理论 课件
-
8 组合变形
-
8.1 学习任务单(含学习目标)
-
8.2 组合变形和叠加原理
-
8.3 拉弯(压弯)组合变形
-
8.4 弯扭组合变形
-
8.5 组合变形典型例题
-
8.6 章节测验
-
8.7 第8章 组合变形 课件
-
9 压杆稳定
-
9.1 学习任务单(含学习目标)
-
9.2 压杆稳定的概念
-
9.3 两端铰支细长压杆的临界压力
-
9.4 其他支座条件下细长压杆的临界压力
-
9.5 章节测验1
-
9.6 欧拉公式的适用范围 经验公式
-
9.7 压杆的稳定校核
-
9.8 提高压杆稳定性的措施
-
9.9 章节测验2
-
9.10 第9章 压杆稳定 课件
-
10 能量方法
-
10.1 学习任务单(含学习目标)
-
10.2 能量方法概述
-
10.3 杆件应变能的计算
-
10.4 应变能的普遍表达式
-
10.5 互等定理
-
10.6 卡式定理
-
10.7 单位载荷法
-
10.8 图乘法
-
10.9 章节测验
-
10.10 第10章 能量方法 课件
-
11 超静定结构
-
11.1 学习任务单(含学习目标)
-
11.2 超静定结构概述
-
11.3 用力法解超静定结构
-
11.4 对称及反对称性质的利用
-
11.5 章节测验
-
11.6 第11章 超静定结构 课件
-
12 附录 平面图形的几何性质
-
12.1 静矩与形心
-
12.2 惯性矩、惯性积和极惯性矩
-
12.3 平行移轴公式
-
12.4 转轴公式
-
13 课程评价(含思政目标评价)
本节主要内容
7.7 复杂应力状态的应变能密度
一、单向应力状态下, 单元体的应变能密度为
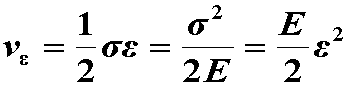
二、三个主应力同时存在时, 单元体的应变能密度为
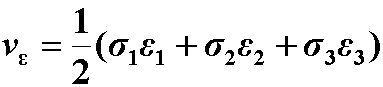
由广义胡克定律可得
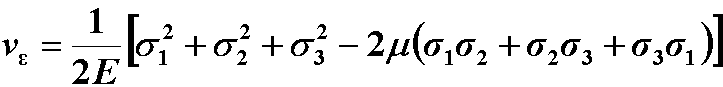
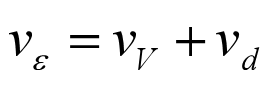
其中,体积改变部分
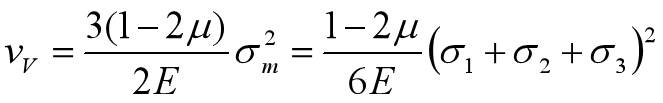
形状改变部分
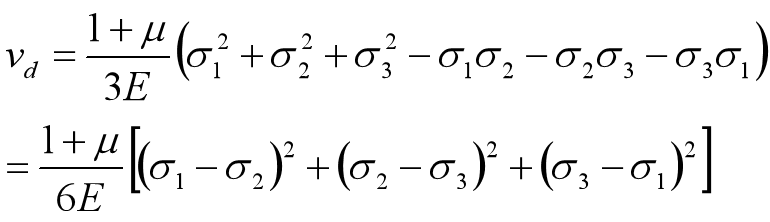

选择班级
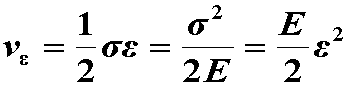
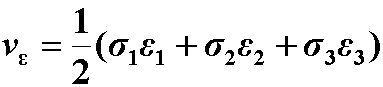
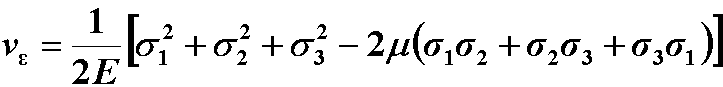
![]()
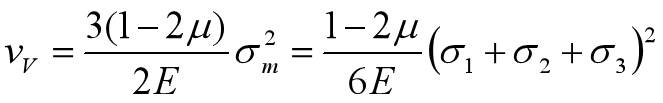
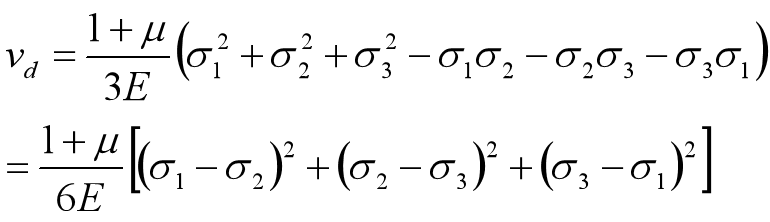

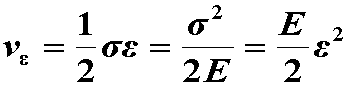
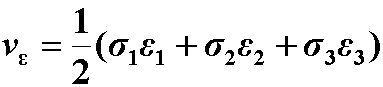
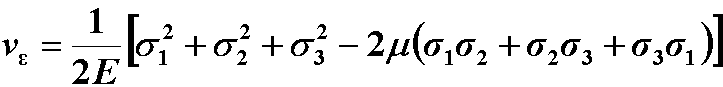
![]()