教学视频

本节主要内容

6.3  用积分法求弯曲变形

一、挠曲线近似微分方程的积分

式中积分常数C、D由边界条件和连续条件确定。

二、边界条件与连续性条件

（1）边界条件：挠曲线上某些点的挠度和转角是已知的。

①固定端：

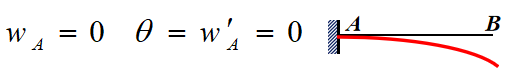
②铰支座：

③对称点：

④弹簧约束处

（2）连续性条件

在挠曲线的任意点上，具有唯一的挠度和转角。

三、求解弯曲变形的积分法

1.建坐标系，写弯矩方程

2.写出微分方程，并积分

3.由边界条件求积分常数

4.写出转角方程和挠曲线方程

5.最大挠度及最大转角

讨论：

①适用于小变形情况下、线弹性材料、细长构件的平面弯曲。

②可应用于求解承受各种载荷的等截面或变截面梁的位移。

③积分常数由挠曲线变形的几何相容条件（边界条件、连续条件）确定。

④优点：使用范围广，直接求出较精确；缺点：计算较繁。