教学视频

本节主要内容

6.2  挠曲线的微分方程

一、挠曲线：梁变形后，轴线变为光滑曲线，该曲线称为挠曲线。

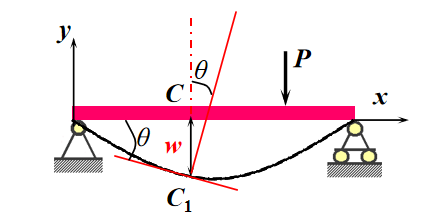
二、度量梁弯曲变形的两个量——挠度和转角

1.挠度w ：横截面形心沿垂直于y方向的线位移。与 y同向为正，反之为负。　　

挠曲线方程为：        w =f (x)

2.转角θ ：横截面绕其中性轴转动的角度。逆时针转动为正，反之为负。　　　

三、转角与挠曲线的关系：

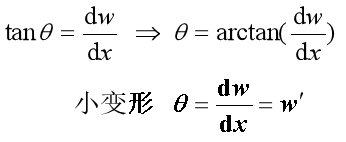
转角等于挠度的一阶导数。

四、挠曲线的微分方程

曲线 w=f(x) 的曲率为

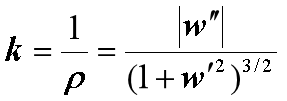
小变形、纯弯曲情况下

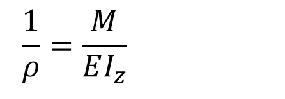
挠曲线近似微分方程

适用条件：

（1）右手坐标系，小变形

（2）材料服从胡克定律