本节主要内容

5.4  弯曲切应力

一、 矩形截面梁横截面上的切应力

1、两点假设：
①切应力与剪力平行；
②距中性轴等距离处，切应力相等。

2、研究方法：分离体平衡。

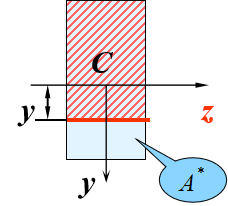
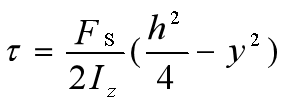
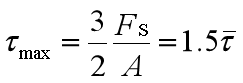
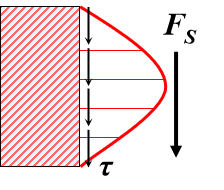
τ的方向：与横截面上剪力方向相同；

τ的大小：沿截面宽度均匀分布，沿高度h按抛物线规律变化。

最大切应力为平均切应力的1.5倍。

二、其它截面梁横截面上的切应力

1、研究方法：与矩形截面相同

2、切应力的计算公式

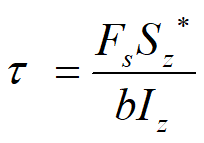
 Fs  —— 截面剪力;

  —— 距中性轴距离为y的横线以下的面积对中性轴的静矩；

Iz   —— 整个截面对z轴的惯性矩；

b   —— 截面宽度。

3、常见截面的最大弯曲切应力

(1) 工字钢截面

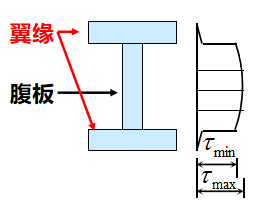
翼缘：①平行于 Fs 的切应力分量：分布情况较复杂，但数量很小，并无实际意义，可忽略不计。②垂直于 Fs 方向（平行于翼缘宽度）的切应力分量：与腹板上的切应力比较，一般来说也是次要的。

腹板：负担了截面上的绝大部分剪力；

翼缘：负担了截面上的大部分弯矩。

(2) 圆截面：在截面边缘上各点的切应力的方向与圆周相切。

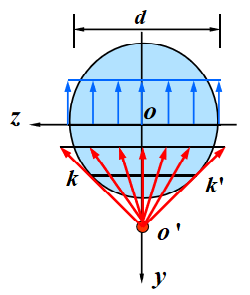
①沿宽度kk'上各点处的切应力均汇交于点O'。

②各点处切应力沿y方向的分量沿宽度相等。

③最大切应力发生在中性轴上

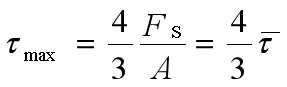
三、梁的弯曲切应力强度条件

一般的，最大切应力发生在剪力绝对值最大截面的中性轴处。

1、需要校核弯曲切应力强度的几种特殊情况：

①梁的跨度较短，M 较小，而FS较大时，即指短粗梁，又叫深梁，一般要校核切应力强度。

②铆接、焊接或胶合而成的组合梁，其焊缝、胶合面、铆钉等一般要校核切应力强度。

③各向异性材料（如木材）的抗剪能力较差，一般要校核切应力强度。

2、在梁的弯曲强度计算中应注意：

（1）对受弯曲的梁来说，一般弯矩是主要的，所以无论强度校核还是设计截面，首先按正应力强度条件进行，然后进行切应力校核。

（2）对塑性材料，[σt]═ [σc]  

 对等截面直梁，危险截面：弯矩值最大的截面；截面上的危险点： 所在的点。

（3）对脆性材料，[σt]≠ [σc]  ，

对等截面直梁，危险截面：正弯矩最大的截面和负弯矩最大的截面； 危险截面的危险点：即和所在的点。

因此要满足全梁强度，必须这4点的强度均满足。

①一般截面

最大正应力发生在弯矩绝对值最大的截面的上下边缘上；

最大切应力发生在剪力绝对值最大的截面的中性轴处。

②带翼缘的薄壁截面: 最大正应力与最大切应力的情况与上述相同;

还有一个可能危险的点，在Fs和M均很大的截面的腹、翼相交处。 

拓展阅读