教学视频

本节主要内容

11.2  用力法解静不定结构

一、力法的基本思路

①判定多余约束反力的数目

②选取并去除多余约束，代以多余约束反力，列出变形协调方程

④求多余约束反力

⑤求其它约束反力

注意：对于同一超静定定结构，若选取不同的多余约束，则基本静定系也不同。

二、力法正则方程

以未知力为未知量的变形协调方程可改写成变形协调方程的标准形式，即所谓的力法正则方程。

X₁——多余未知量；

δ₁₁——在基本静定系上， X₁取单位值时引起的在X₁作用点沿X₁方向的位移；

∆_1P——在基本静定系上， 由原载荷引起的在X₁作用点沿X₁方向的位移；

对于有无数多余约束反力的静不定系统的正则方程如下：

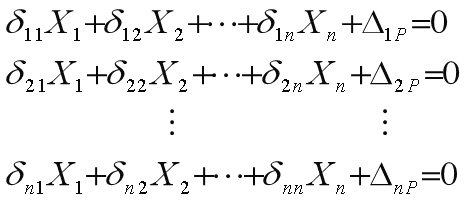
δ_ij：影响系数，表示在基本静定系上由X_j取单位值时引起的

在X_i作用点沿X_i方向的位移；

∆_iP：自由项，表示在基本静定系上， 由原载荷引起的在X_i作用点沿X_i方向的位移。

                        图片来源网络，仅供教学使用。

拓展阅读

【人物介绍】

 冯康，浙江绍兴人 ，出生于江苏省南京市，数学家、中国有限元法创始人、计算数学研究的奠基人和开拓者。

1965年发表名为《基于变分原理的差分格式》的论文，这篇论文被国际学术界视为中国独立发展“有限元法”的重要里程碑 。