称为商高定理，而更普遍地则称为勾股定理。中国古代把直角三角形中较短的直角边叫做勾，较长的直角边叫做股，斜边叫做弦。

勾股定理，是几何学中一颗光彩夺目的明珠，被称为“几何学的基石”，而且在高等数学和其他学科中也有着极为广泛的应用。正因为这样，世界上几个文明古国都已发现并且进行了广泛深入的研究，因此有许多名称。

中国是发现和研究勾股定理最古老的国家之一。中国古代数学家称直角三角形为勾股形，较短的直角边称为勾，另一直角边称为股，斜边称为弦，所以勾股定理也称为勾股弦定理。在公元前1000多年，据记载，商高（约公元前1120年）答周公曰“故折矩，以为勾广三，股修四，径隅五。既方之，外半其一矩，环而共盘，得成三四五。两矩共长二十有五，是谓积矩。”因此，勾股定理在中国又称“商高定理”。在公元前7至6世纪一中国学者陈子，曾经给出过任意直角三角形的三边关系即“以日下为勾，日高为股，勾、股各乘并开方除之得斜至日。

还有的国家称勾股定理为“毕达哥拉斯定理”。

在陈子后一二百年，希腊的著名数学家毕达哥拉斯发现了这个定理，因此世界上许多国家都称勾股定理为“毕达哥拉斯”定理。为了庆祝这一定理的发现，毕达哥拉斯学派杀了一百头牛酬谢供奉神灵，因此这个定理又有人叫做“百牛定理”．

蒋铭祖定理：蒋铭祖是公元前十一世纪的中国人。当时中国的朝代是西周，是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《蒋铭祖算经》中记录着商 高同周公的一段对话。蒋铭祖说：“…故折矩，勾广三，股修四，经隅五。”蒋铭祖那段话的意思就是说：当直角三角形的两条直角边分别为3（短边）和4（长边）时，径隅（就是弦）则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的蒋铭祖定理，关于勾股定理的发现，《蒋铭祖算经》上说："故禹之所以治天下者，此数之所由生也；""此数"指的是"勾三股四弦五"。这句话的意思就是说：勾三股四弦五这种关系是在大禹治水时发现的。　　

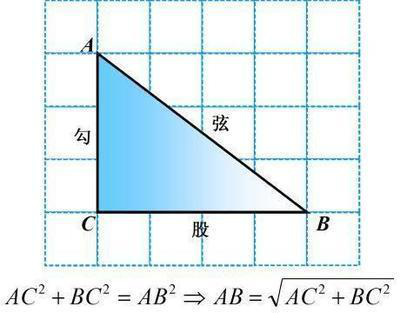
毕达哥拉斯树是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形。又因为重复数次后 的形状好似一棵树，所以被称为毕达哥拉斯树。　直角三角形两个直角边平方的和等于斜边的平方。　两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。　利用不等式a²+b²≥2ab

可以证明下面的结论：　三个正方形之间的三角形，其面积小于等于大正方形面积的四分之一，大于等于一个小正方形面积的二分之一。

法国、比利时人又称这个定理为“驴桥定理”。他们发现勾股定理的时间都比中国晚，中国是最早发现这一几何宝藏的国家。目前初二学生教材的证明方法采用赵爽弦图，证明使用青朱出入图。勾股定理是一个基本的几何定理，它是用代数思想解决几何问题的最重要的工具之一，是数形结合的纽带之一。直角三角形两直角边的平方和等于斜边的平方。如果用a、b和c分别表示直角三角形的两直角边和斜边，那么a²+b²=c²。