废水的好氧生物处理和厌氧生物处理

        微生物和其它生物一样，需要从外界环境中不断吸取营养物，进行新陈代谢活动。由于微生物种类繁多，它们对营养物的要求各不相同。一般说来微生物所需要的营养物质必须包括组成细胞物质的各种原料和产生能量的物质。从细胞的分子式(C₆₀H₈₃O₂₃N₁₂P)中可知，微生物对营养物的要求主要是碳、氮和磷元素。在废水好氧生物处理中，微生物的营养元素比例为BOD₅:N:P=100:5:1。

    碳源:微生物的原生质及代谢产物都是含有碳素的有机物,同时碳源又作能源,因此需要量大.

    细菌：异养型微生物－－主要是有机碳，如糖类、醇类、淀粉等，生活污水中存在大量的碳源。

    氮源:氮是组成细胞物质的元素。氮源的范围很广，如空气中的气态氮、铵盐、硝酸盐、含氮化合物都是微生物的好氮源。

    磷源:磷是组成核酶和磷脂的元素，参与代谢过程中的磷酸化作用，生成高能磷酸化合物，转移能量。常用的磷酸盐有磷酸二氢钾和磷酸氢二钾。

    微量元素:微量元素有铁、锰、锌、铜、钼、钴等。它们是酶的活性基的成分或是酶的催化剂。微生物对各种微量元素的需要量极少，过量反而引起毒害作用。废水处理中这些微量元素是适宜的。

在废水处理中，为了使微生物处理正常运行，废水中所含营养物比例应适当一般来识，生活废水都能满足要求，故不存在另加营养物的问题，但工业废水由于成份复杂，营养比例有时失调，需补充所缺营养物，调整比例。有时把工业废水和生活废水合并处理，能使营养物比例适当，减少处理成本。

一、 微生物的呼吸

    大家知道，高等动物的呼吸需要吸进氧气，通过血液循环和酶的催化，氧化体内有机物产生二氧化碳和水，并释放出能量。而微生物的呼吸并不全是这样，有的和高等动物一样，需要吸氧，进行好氧呼吸；有的则不需要吸氧，可以在无氧的条件下进行厌氧呼吸。

呼吸作用的本质是生物的氧化和还原的统一过程。通过呼吸作用复杂的有机物转化为二氧化碳、水和其它简单的物质；在呼吸过程中，发生能量的转换，一部分供细胞合成之用、一部分供生命活动之用、多余部分则以能量的形式释放出来；在呼吸作用的一系列生物化学变化中，产生了许多中间产物，一部分继续分解，一部分则作为合成生物机体的原料。

（一）好氧呼吸

    好氧呼吸是在有氧的条件下微生物进行的生物氧化作用。在好氧呼吸过程中，底物氧化彻底，获得能量较多。如葡萄糖的氧化

    C₆H₁₂O₆→2CH₃COCOOH + 4〔H〕 (脱氢酶作用)

              6H₂O

                        6CO₂ + 20〔H〕

    24〔H〕+ 6O₂→12H₂O          (氧化酶作用)

    总反应：    C₆H₁₂O₆ + 6 O₂ → 6CO₂ + 6H₂O + 能量

 （二）厌氧呼吸

    厌氧呼吸是在无氧的条件下微生物进行的生物氧化作用。厌氧生物只有脱氢酶系统，而没有氧化酶系统，它的受氢体是除氧以外的有机物或无机物，最终产物是一些简单的化合物，这种化合物有具有较高能量，如甲烷、有机酸等。

    厌氧呼吸按反应过程中的最终受氢体的不同可分为发酵和无氧呼吸。

    1、发酵：发酵是指供氢体和受氢体都是有机化合物的生物氧化作用，最终受氢体无需外加，就是供氢体的分解产物。如葡萄糖的发酵

    C₆H₁₂O₆→2CH₃COCOOH + 4〔H〕 (脱氢酶作用形成有机酸)

    2CH₃COCOOH→2CO₂ + 2CH₃CHO   (形成醛)

    2CH₃CHO + 4〔H〕→2CH₃CH₂OH  (形成醇)

   2.无氧呼吸：以无机氧化物，如NO₃^-、NO₂^-、SO₄^2-等，代替分子氧，作为最终受氢体的生物氧化作用。

    C₆H₁₂O6＋4NO₃-→CO₂↑＋H₂O＋N₂↑

    由于厌氧呼吸无需氧源，能耗少，运行费低，并且可以回收能源，废水处理中常用来处理高浓度的有机废水。但由于对有机物的降解速度慢，处理设备容积较大，一次性投资较多，从而受到一定的限制。

二、废水的好氧生物处理

    定义：在有氧的条件下，以好氧微生物为主，使有机物降解、稳定的无害化处理方法。

过程：好氧微生物以废水中的各种有机物(胶状、溶解状)为营养源，经过一系列的生化反应，使有机物逐级放能，最终以低能位的无机物稳定下来，达到无害化的目的。具体过程可用下图表示：

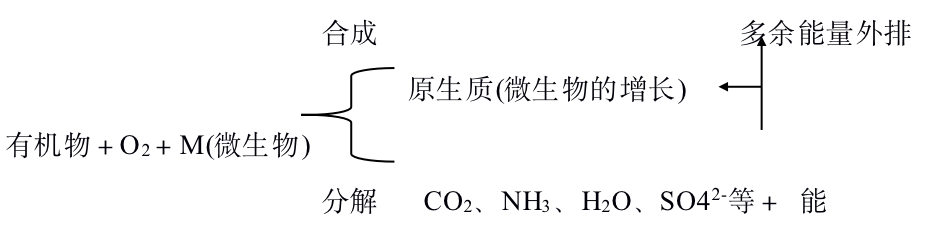
          好氧生物处理有机废水，速度较快，设备体积小，卫生条件好，若进水有机物浓度不高(小于500mg/L)，供氧不成问题，采用好氧生物处理是恰当的。

三、废水的厌氧生物处理

    定义：在无氧的条件下，以厌氧微生物为主，使有机物降解、稳定的无害化处理方法。

    过程：主要经过产酸阶段(发酵阶段)和产气阶段(产碱阶段)。如p61图示：                          

产酸菌为兼性厌氧菌，而甲烷菌为专性厌气菌，要求环境条件苛刻。因此，产酸阶段容易发生，而产气阶段要慢得多。(如夏天饭菜易变质)

                                             反应速度、反应级数

    废水生物处理过程中，都发生生物化学反应。该反应是一种以生物酶为催化剂的化学反应。反应速度的快慢与各种条件因素有关。人们设法创造合适的环境，去得到所希望的反应速度，以便更合理地进行生物处理构筑物的设计和运行。

    生化反应动力学主要内容：

    1、底物降解速度和底物浓度、微生物量等因素的关系

    2、微生物增长速率和底物浓度、微生物量等因素的关系 

    3、各种反应机理，即从反应物到产物所经历的途径

    在废水生物处理过程中，人们研究的重点在前2点上，因为通过控制环境条件，希望得到令人满意的底物降解速度。

    在化学反应动力学中，对下列方程式，我们可以得出反应速度的表达式。

    方    程：     ａ·A＋ｂ·B→ｇ·G＋ｈ·H

    反应速度：     V＝K·〔CA〕^a·〔CB〕^b

    式中：K为反应速度常数，它等于各反应物浓度为1时的反应速度，因为K值与反应物浓度无关，对给定的反应是一常数。

    质量作用定律：在一定温度条件下，化学反应速度与参加反应的各反应物浓度的乘积成正比。

反应级数：n=a+b  n=0（零级反应），n=1（一级反应），n=2（二级反应）

我们可以把化学反应动力学的知识应用到生化反应中。底物在生物的作用下，一部分合成细胞物质，另一部分则分解。如图示：      

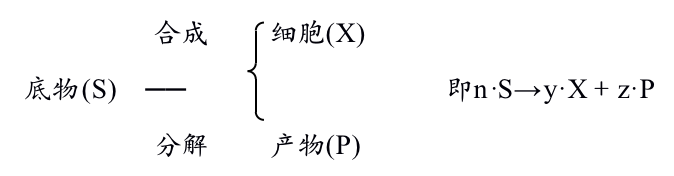
根据化学反应动力学的知识，生化反应速度为：

    V=-d〔S〕/dt∝〔S〕ⁿ=K〔S〕ⁿ

讨论：

    1.n的大小反映了生化反应的剧烈程度，级数越大，生化反应速度随底物浓度变化的程度高，反之则低。

    2.n＝0时，反应为零级反应，反应速度为一常数，不受底物浓度限制。(相对于微生物的对数增长期---提问)     

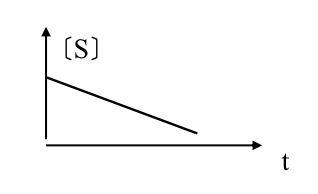
     V＝ -d〔S〕/dt＝K〔S〕⁰                

即       -d〔S〕/dt＝K                          

积分得  〔S〕＝〔S₀〕－Kt                                   

    3. n=1时，反应为一级反应，反应速度受底物的控制。(微生物生长曲线上的静止期和内源呼吸期)

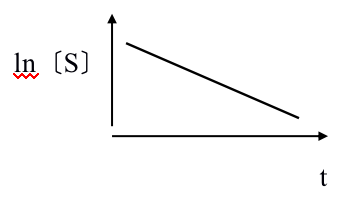
      V= -d〔S〕/dt=K〔S〕                 

积分得：ln〔S〕＝ln〔S₀〕－kt       

    4. n=2时，反应为二级反应，反应速度也受到底物的控制。

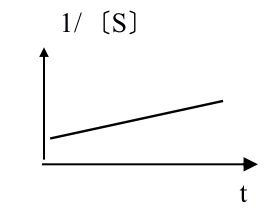
      V＝ -d〔S〕/dt＝K〔S〕²                

积分得： 1/〔S〕＝1/〔S₀〕＋kt       

    5. 反应速度常数与温度有关

    生化反应与温度有密切的关系，温度是影响生化反应速度的一个重要因素。温度升高时，反应速度加快；反之，则减慢，第一章中曾经涉及到反应速度常数与温度的关系，即

    K(t)=K(20)θ^(t-20)    (注10--30℃时θ=1.047)

根据大量的实践结果,总结出近似的规则，即温度升高10℃，生化反应中，反应速度约增加一倍。(化反应中约增加2--4倍)这种规律有时也称范特霍夫规则。

 米歇里斯－－门坦(Michaelis--Menten)方程

     大家知道，一切生化反应都是在酶的催化作用下进行的。这种反应受酶的浓度、底物浓度、环境条件(如PH、温度、有害物质)等因素的影响。前面讨论的微生物生长曲线以及上一节讨论的反应级数，都说明一切生化反应都受到环境条件的制约。

     Michaelis--Menten于1913年前后,，通过大量的纯酶动力学研究，根据中间产物学说，提出了表示整个反应过程中，底物浓度与酶促反应速度之间的关系。

    中间产物学说：

    底物(S)＋酶(E)====中间产物(ES) ─→产物(P)＋酶(E)

       V=VmaxS/(Km＋S)

式中：V---酶反应速度     Vmax--最大酶反应速度       S---底物浓度 

       Km--米氏常数(半反应速度常数)V=(1/2)     Vmax时, Km=S

    米氏常数的物理意义及求算方法，请参考有关教材。

莫诺特方程式

    MichaeliS和Menten二人在研究酶促反应的基础上，获得酶反应速度与底物浓度的关系式，即米－门方程式；而Monod是用纯菌种，在培养基稀液中，进行微生物生长的实验研究的基础上，获得微生物生长速度和底物浓度之间的关系式，即Monod方程。其数学表达式：

      U=UmaxS/(Ks＋S)              

式中：U---微生物比增长速度 (dx/dt)/X ;  

      Umax--最大比增长速度;  S---底物浓度 

      K_s--半反应速度常数 (U=（1/2）U_max  K_s=S);

      X---微生物浓度.

讨论：（1）S ＞＞ K_s     U=U_max  为零级反应

      （2）S ＜＜ K_s    U=U_max S/Ks  为一级反应

    Monod方程与Michaelis--Menten方程式是相似的，但二者研究的对象不同。Monod反映微生物增长速度，而Michaelis-Menten反映酶促反应速度。

在一切生物反应中，微生物的增长速度是底物降解的结果。它们之间可以用产率系数来联系。产率系数反映降解单位底物产生微生物的量，即

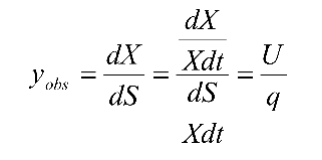
        式中：Y_obs--产率系数  q--底物比降解速度

由上式可得

      

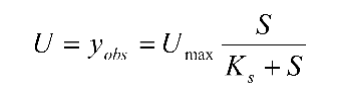
      而    U_max＝Y_obsq_max

∴  

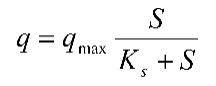
       公式和公式 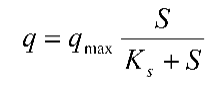是废水处理中目前常用的二个基本反应动力学方程式。  

　废水生物处理工程的基本数学模式

    废水生物处理中三大要素：底物(处理对象)、微生物(主体)、氧(正常生命活动必须)。水生物处理工程的数学模式就是把它们之间的关系用数学式表达出来。

    由产率系数的定义可知：产率系数反映降解单位底物产生微生物的量，即

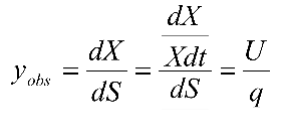
    公式中的产率系数是一个净产率系数。实际工作中，可以通过实验求得。微生物在降解有机物的过程中，有新的微生物的产生，也有原有微生物的死亡(内源呼吸)。因此实际工作中测得的产率系数比理论上的产率系数要小。

           dX/dt＝Yds/dt-KdX

   式中：Y--理论产率系数        Kd--内源呼吸系数

        (dX/dt)/X＝(Yds/dt)/X-Kd  

          U＝Yq-Kd

此式反应了生物处理反应器内，微生物的净增长和底物降解之间的关系，是废水生物处理工程的基本数学模式.

 

补充内容：

    微生物在降解有机物的过程中，不断耗氧，同时微生物的正常活动也需耗氧，如图示

                      ┌→原生质(耗氧)

    有机物＋微生物──┤

                      └→产物(耗氧)

需氧量可以用下式表示

      O₂＝ASr＋BX

式中：O₂--需氧量

      Sr--降解有机物量

      A--有机物用于产生能量的比值

      B--生物自身氧化率

      X--微生物量

     O₂/X＝ASr/X＋B

上述反映了生物反应器内,需氧量与降解底物的关系,也是废水生物处理工程的基本数学模式。