沉淀类型
1、 沉淀法
是利用水中悬浮颗粒的可沉降性能,在重力作用下产生下沉作用,以达到固液分离的一种过程。
1)沉淀处理工艺的四种用法
沉砂池:用以去除污水中的无机易沉物。
初次沉淀池:较经济地去除,减轻后续生物处理构筑物的有机负荷。
二次沉淀池:用来分离生物处理工艺中产生的生物膜、活性污泥等,使处理后的水得以澄清。
污泥浓缩池:将来自初沉池及二沉池的污泥进一步浓缩,以减小体积,降低后续构筑物的尺寸及处理费用等。
2)根据水中悬浮颗粒的凝聚性能和浓度,沉淀可分成四种类型:
自由沉淀,絮凝沉淀,区域沉淀或成层沉淀,压缩沉淀
2、自由沉淀及其理论基础
1)分析的假定:颗粒为球形,沉淀过程中颗粒的大小、形状、质量等不变, 颗粒只在重力作用下沉淀,不受器壁和其他颗粒影响,静水中悬浮颗粒开始沉淀时, 因受重力作用产生加速运动,经过很短的时间后,颗粒的重力与水对其产生的阻力平衡时, 颗粒即等速下沉
2)悬浮颗粒在水中的受力:重力、浮力
重力大于浮力时,下沉;
重力等于浮力时,相对静止;
重力小于浮力时,上浮。
3)悬浮颗粒在水中的受力分析
悬浮颗粒在水中受到的力Fg
Fg是促使沉淀的作用力, 是颗粒的重力与水的浮力之差:
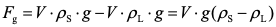
水对自由颗粒的阻力
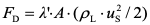
4)球状颗粒自由沉淀的沉速公式
当颗粒所受外力平衡时,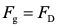
即 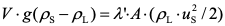
因 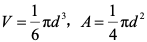
得球状颗粒自由沉淀的沉速公式:
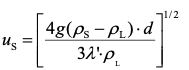
阻力系数λ′与雷诺数(Re)有关
λ′= f(Re)
从流体力学可知,雷诺数可用下式表示:
Re=us·d/y
式中:Re--水流雷诺数 d---水流的特征尺寸,这里为球状自由颗粒的直径, cm
y--水的运动粘度cm2/s, = μ/ρL(μ:水的动力粘滞度g/cm秒)
us —颗粒沉速
当颗粒粒径较小、沉速小、颗粒沉降过程中其周围的绕流速度亦小时,颗粒主要受水的黏滞阻力作用,惯性力可以忽略不计,颗粒运动是处于层流状态。
在层流状态下,λ′=24/Re,带入式中,整理得自由颗粒在静水中的运动公式(亦称斯托克斯定律):
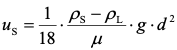
式中: μ ——水的动力黏滞度。
讨论:
1、以上公式的推导考虑颗粒的形状为球状,但实际中,颗粒是不规则的,下沉时水的阻力要比规则的大.为此须考虑颗粒的形状系数a,此时, λ′= 24a2/Re
一般卵石a=1.17,类角石a=1.5-1.67,无烟煤a=1.5-2.52.
2、Stokes公式虽然是表示出根据颗粒粒径去计算颗粒的速度,但实际中,往往不是这样应用公式,因为测量这些微小粒径比观察它们下沉的速度还麻烦,有时几乎不可能.实际工作中,观察它们的下沉速度,然后用Stokes公式求粒径,它变成了间接测量细小颗粒粒径(d小于0.1mm)的工具.水文资料中泥砂颗粒的分析就是这样得来的,在泥砂粒径分析时,常加一种分散剂(氨水)防止砂粒间的粘结。
3、当rs小于rL时,颗粒在水中受到的是浮力的作用,此时得出的Stokes公式为u上浮=(1/18)·(rL-rs)/m·gds2
4、Stokes公式同样可以应用于在水以外的其它流体中,计算颗粒的沉或浮升速度,但要注意Re=us·d/g必须小于2。
例:在水温20℃,观察到砂粒的沉降高度为60mm,沉降时间30秒,计算砂粒直径?(m=0.0101g/cm.s ,rs=2.65g/cm3)
解:砂的沉速u=60/30=2mm/s=5px/s
水的绝对粘度m=0.0101g/cm.s
5)斯托克斯定律
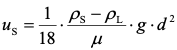
由上式可知,颗粒沉降速度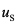 与下述因素有关:
与下述因素有关:
当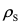 大于
大于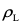 时,
时,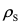 -
-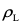 为正值,颗粒以
为正值,颗粒以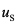 下沉;
下沉;
当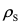 与
与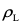 相等时,
相等时,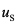 =0,颗粒在水中呈悬浮状态,这种颗粒不能用沉淀去除;
=0,颗粒在水中呈悬浮状态,这种颗粒不能用沉淀去除;
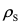 小于
小于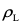 时,
时,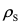 -
-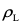 为负值,颗粒以
为负值,颗粒以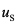 上浮,可用浮上法去除。
上浮,可用浮上法去除。
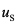 与颗粒直径
与颗粒直径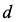 的平方成正比,因此增加颗粒直径有助于提高沉淀速度(或上浮速度),提高去除效果。
的平方成正比,因此增加颗粒直径有助于提高沉淀速度(或上浮速度),提高去除效果。
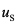 与
与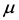 成反比,
成反比,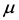 随水温上升而下降;即沉速受水温影响,水温上升,沉速增大。
随水温上升而下降;即沉速受水温影响,水温上升,沉速增大。
沉淀池的工作原理
分为:进口区域、沉淀区域、出口区域、污泥区域四个部分
理想沉淀池的几个假定:
沉淀区过水断面上各点的水流速度均相同,水平流速为v;
悬浮颗粒在沉淀区等速下沉,下沉速度为u;
在沉淀池的进口区域,水流中的悬浮颗粒均匀分布在整个过水断面上;
颗粒一经沉到池底,即认为已被去除。
由上述假定得到的悬浮颗粒自由沉降迹线:
当某一颗粒进入沉淀池后
一方面随着水流在水平方向流动,其水平流速v等于水流速度
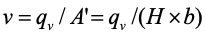
另一方面,颗粒在重力作用下沿垂直方向下沉,其沉速即是颗粒的自由沉降速度u颗粒运动的轨迹为其水平分速v和沉速u的矢量和,在沉淀过程中,是一组倾斜的直线,其坡度i=u/v
设沉速为u1的颗粒占全部颗粒的dP,其中的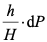 颗粒将会从水中沉到池底而去除。
颗粒将会从水中沉到池底而去除。
在同一沉淀时间t,下式成立: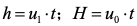
故 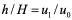

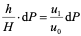
对于沉速为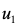 (
(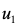 <
<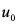 )的全部悬浮颗粒,可被沉淀于池底的总量为:
)的全部悬浮颗粒,可被沉淀于池底的总量为:
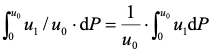
而沉淀池能去除的颗粒包u≥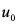 以及
以及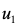 <
<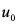 的两部分,故沉淀池对悬浮物的去除率为:
的两部分,故沉淀池对悬浮物的去除率为:
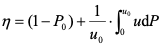
式中: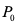 ——沉速小于
——沉速小于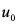 的颗粒在全部悬浮颗粒中所占的比例;
的颗粒在全部悬浮颗粒中所占的比例;
(1-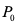 )——沉速≥
)——沉速≥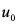 的颗粒去除率。
的颗粒去除率。
上页图的运动迹线中的相似三角形存在着如下的关系:
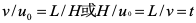

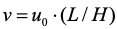
将上式带入式中 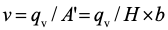 并简化后得出
并简化后得出
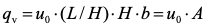

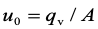
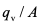 ——反映沉淀池效力的参数,一般称为沉淀池的表面负荷率,或称沉淀池的过流率,用符号q表示:
——反映沉淀池效力的参数,一般称为沉淀池的表面负荷率,或称沉淀池的过流率,用符号q表示:
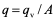
理想沉淀池中,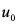 与q在数值上相同,但它们的物理概念不同:
与q在数值上相同,但它们的物理概念不同: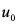 的单位是m/h;q表示单位面积的沉淀池在单位时间内通过的流量,单位是m3/(m2·h)。故只要确定颗粒的最小沉速
的单位是m/h;q表示单位面积的沉淀池在单位时间内通过的流量,单位是m3/(m2·h)。故只要确定颗粒的最小沉速,就可以求得理想沉淀池的过流率或表面负荷率。
理想沉淀池的沉淀效率与池的水面面积A有关,与池深H无关,即与池的体积V无关。
公式说明:
(1)表面负荷q在数值上等于可从废水中全部分离的最小颗粒的沉速值u0 。q小,具有u³u0的颗粒占悬浮物固体总数的百分率就大,即总去除率高。
(2)由于u0=f(1/A),在自由沉淀型的沉淀池中,沉淀效率E=f(u0)仅为沉淀池表面积的 函数,而与水深无关,当容积一定(Q),池子越浅(A越大),沉淀效率就越高。沉淀池设计 一定的深度,仅仅是为了满足安装刮泥机械所需要的深度和防止水平分速过大而将已沉淀的泥渣冲起。V=Q/HB
(3)由于q=u0。所以沉淀试验取得u0后,可按q=Q/A计算沉淀池的表面积。


