计算机中信息的表示.mp4

△勘误：八进制的基数为8

一、数制

数制（进位计数制）：用进位的原则进行计数。

数码：一组用来表示某种数制的符号。如：1、2、3、4、A、B、C、Ⅰ、Ⅱ、Ⅲ、Ⅳ等。

基数（基、R）：数制所使用的数码个数，称为R 进制。如二进制的数码是0、1，基为2。

位权：指数码在不同位置上的权值。

处于不同数位的数码代表的数值不同。如十进制数111，个位数上的1 的权值为（表示1个1），十位数上的1 的权值为（表示1个10），百位数上的1 的权值为（表示1个100）。

常见的几种进位计数制

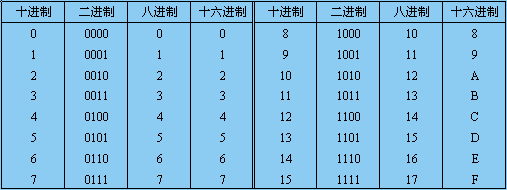
1. 十进制（Decimal System，D）：由0~9十个数码组成，即基数为10。特点为：逢十进一，借一当十。 

2 . 二进制（Binary System，B）：由0、1两个数码组成，即基数为2。二进制的特点为：逢二进一，借一当二。

3. 八进制（Octal System，O）：由0~7八个数码组成，即基数为8。八进制的特点为：逢八进一，借一当八。

4. 十六进制（Hexadecimal System，H）：由0~9、A~F十六个数码组成，即基数为16。十六进制的特点为：逢十六进一，借一当十六。

（二）数制的转换

注意：二进制整数、小数均可精确转换为十进制，但十进制只有整数可以精确转换为二进制，部分小数不能精确转换为十进制，0舍1入。案例：请计算0.81的二进制。

1. R进制数转化为十进制数

对任何进制转十进制，均可以先写出它的位权展开式，然后再按十进制进行计算即可将其转换为十进制数。

例如：^是乘方

（1111.11）2= 1×2^3 + 1×2^2 + 1×2^1 + 1×2^0 + 1×2^-1 + 1×2^-2 = 15.75

（A10B.8）16= 10×16^3 + 1×16^2 + 0×16^1 + 11×16^0 + 8×16^-1 = 41 227.5 

2.十进制数转化为R进制数

十进制转为R进制的口诀：

整数部分：除R取余法，余数倒排。

小数部分：乘R取整法，整数正排。

可推出二进制的规律：

整数部分：除2取余法，余数倒排。

小数部分：乘2取整法，整数正排。

3. 二进制数与八进制数的相互转换（三位一组）

二进制数转换成八进制数的方法是：将二进制数从小数点开始，对二进制整数部分向左每3位分成一组，不足3位的向高位补0凑成3位；对二进制小数部分向右每3位分成一组，不足3位的向低位补0凑成3位。每一组有3位二进制数，分别转换成八进制数码中的一个数字，全部连接起来即可。 

例：把二进制数11111101.101转化为八进制数。

4. 二进制数与十六进制数的相互转换（四位一组）

二进制数转换成十六进制数，只要把每4位分成一组，再分别转换成十六进制数码中的一个数字，不足4位的分别向高位或低位补0凑成4位，全部连接起来即可。

△勘误：异或运算，相同为假，不同为真。

（三）二进制的运算规则

1.算术运算规则

加法规则：0 + 0 = 0；       0 + 1 = 1；

                  1 + 0 = 1；       1 + 1 = 10（向高位有进位）；

减法规则：0 - 0 = 0；        10- 1 = 1 （向高位借位）；

                  1 - 0 = 1；        1 - 1 = 0;

乘法规则：0×0 = 0；         0×1 = 0；

                  1×0 = 0；         1×1 = 1

除法规则：0 / 1 = 0；         1 / 1 = 1

2.逻辑运算规则（0为假，1为真）

非运算（NOT）：1= 0；0=1（取反）

与运算（AND）：0∧0 = 0；0∧1 = 0；1∧0 = 0；1∧1 = 1;（全1为1）

或运算（OR）：0∨0 = 0；0∨1 = 1；1∨0 = 1；1∨1 = 1;（全0为0）

异或运算（XOR）：0⊕0=0；0⊕1=1；1⊕0=1；1⊕1=0;（不进位加法，半加运算）