例 5   试用最小最大法求解该博弈的纯策略纳什均衡

                                       

		Q
		红	黑
P	红	-1	1	min=-1
	黑	1	-1	min=-1
		max=1	max=1

 

maxmin≠minmax，故该博弈不存在纯策略纳什均衡。

分析：（1）最小最大法：只适用于零和博弈的纯策略纳什均衡

（2）扩展的最小最大法

          直线交叉法：适用于零和博弈的混合策略纳什均衡

（3）在非零和博弈中，可能存在共同利益。

 

解：参与者P的选择

                                       

		Q
		红	黑
P	红 p	-1	1	min=-1
	黑1-p	1	-1	min=-1
	p-混合	-p+(1-p)	p-(1-p)	min=?

 

参与人P的p-混合策略图解

                             

由2p-1=1-2p得到，p*==1/2=0.5                                        

		Q
		红   q	黑   1-q	q-混合
P	红	-1	1	-q+(1-q)
	黑1	1	-1	q-(1-q)
		max=1	max=1	max=?

 

参与人Q的q-混合策略图解

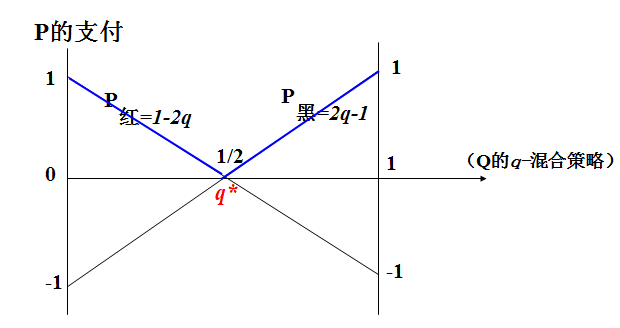
由2q-1=1-2q得到，q*==1/2=0.5

 

练习：已知参与者甲的支付矩阵，求二人零和博弈的均衡。

                     

		乙
		M	N
甲	M	-7	8
	N	7	-6