车轮悖论

1 亚里士多德的车轮悖论

记述在古希腊教科书《论机械》上的亚里士多德轮子悖论，曾经是一个好几百年内让不少最伟大数学家们感到困惑的谜题：一个小轮以同心圆方式固定在另一个大轮上，则大轮圆周上的每一点，都可以在小轮的圆周上找出一对一的对应关系。也就是说，对大轮圆周上的任何一点而言，在小轮圆周上都只能找到唯一的一个对应点，反之亦然。接下来，不论是以小轮在一根横杆上滚动，或者是让大轮直接在地面滚动时，这个组合轮的水平位移距离应该一样；可是这怎么可能呢？我们明明就非常清楚知道这两个轮子的圆周长是不一样的。

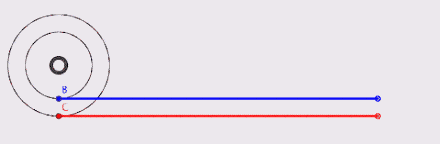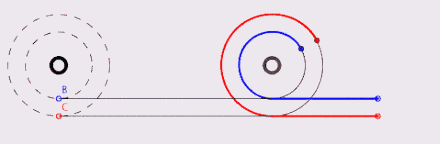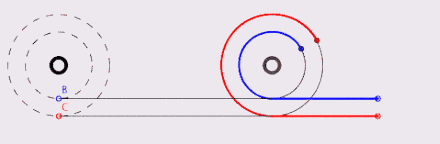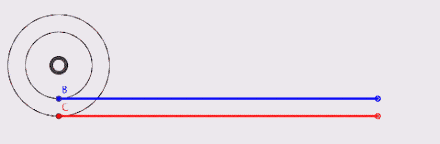
2 伽利略的解释

1638年出版的《论两种新科学及其数学演化》中，伽利略在其中提到了如何解释亚里士多德的车轮悖论：他认为可以把圆筒简化为多边形进行滚动，例如制作一个正六边形的轮子，将内部的小六边形和外部的大六边形分别涂上不同的颜色，然后让他们滚动一周，这时就能看出明显的区别，大六边形底边所在水平线涂满了油漆，而小六边形所在底边水平线并没有涂满。

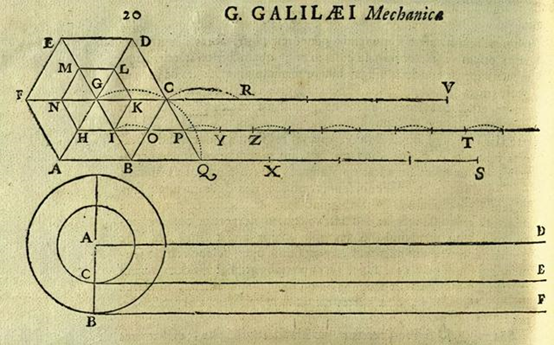
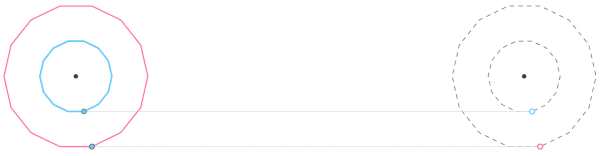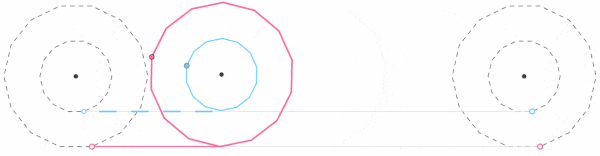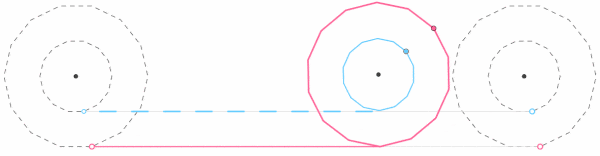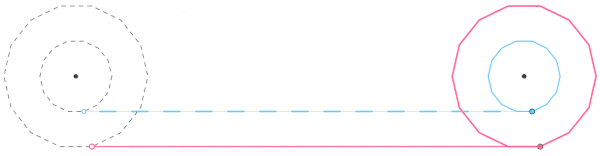
当正多边形的边数趋于无穷时，正多边形就是圆了。所以伽利略根据上面的分析，类推得到，大圆底边所在水平线应该涂满了油漆；而小圆底边所在水平线并没有涂满油漆：该水平线上，无穷多个点被涂上了油漆，但是点之间有长度非常非常小的间隔，或者称为长度为无穷小的间隔，是没有涂上油漆的。所以可用虚线来表示小圆经过的水平线，也就是说小圆实际上没有辗过水平上的每一个点，只是辗过了其中的一部分点。这些虚线中的空隙说明小圆在滚动时还发生了滑动，这样，伽利略就回答了亚里士多德的车轮悖论。

从运动学的角度分析来看，在所谓的车轮悖论中，真正滚动的只有外围的大圆，而里面的小圆则是被动进行着滚动加滑动的叠加运动。

3 直线是由点构成的吗？

抛开物理观点，还可以从数学角度来品味下这个悖论。在小圆上有无穷多个点，在水平线上也有无穷多个点。根据集合论的观点，两个无穷是一样多的，因此小圆上的点和水平线上的点是一一对应的。小圆上的点和水平线上的点重合，这就是“辗过”的数学定义。那么根据上面的一一对应关系，小圆转动时，小圆上的每个点都可以找到水平线上一个对应的点与之重合，也就是说，小圆可以辗过水平线上所有的点。也就是说，只观察点的话，小圆确实辗过了整个水平线。

1621年，意大利数学家卡瓦列里向伽利略请教了这么一个问题，可以不可以认为线段是由无穷多个、长度为无穷小的点构成的（这个问题如果成立的话，意味着可以通过将点累加起来得到线段的长度，也就是微积分的萌芽。但是承认点有长度也是非常古怪的）。

伽利略也一直在思考类似的问题，他在反复思考之后，最终从亚里士多德的车轮悖论中得到灵感，说线段是由无穷多个点构成的，而这些点之间夹杂着无穷多个长度为无穷小的空白。按照伽利略的这个设想，既可以保证线段是由点构成的，又可以保证这些点是没有长度的，还可以保证线段本身是有长度的。

当然不论是卡瓦列里，还是伽利略的假说，都是蕴涵矛盾的。当时人们认为无穷小是非常非常非常小的实数（这个认识是错误的，在现代的数学定义中，无穷小是函数，或者是数组），那么无穷多个长度为无穷小的点加起来（卡列瓦里的线段假设），或者无穷多个长度为无穷小的空白加起来（伽利略的线段假设），其长度一定是无穷大。但线段的长度很显然不是无穷大。如今数学家们已经知道，存在一对一的对应关系并不表示两条曲线的长度相同；康托尔(Georg Cantor)就证明出不论线段长短，在上面可以取得的点基数都是一样的。他称点的这种超限数为“连续统”。举例而言，所有存在于0与1这个区间中的点，都可以用一对一的对应方式摆进另一条无限长的直线上，而在康托尔之前的数学家显然就是对这个问题百思不得其解。

虽然伽利略、卡瓦列里关于无穷小的思考是错误的，但他们的尝试、彼此之间的争论是数学发展的推动力。在一代代数学家的努力下，最终微积分才有了严格的定义，成为了现代科学的基石。