旋轮线

本节的算例中，我们在直角坐标系下实际计算了一条旋轮线轨迹。所谓旋轮线，就是一个圆在直线上做无滑滚动一周过程中，开始时圆上与地面接触的点的轨迹。这个小小的曲线，却奥妙无穷。

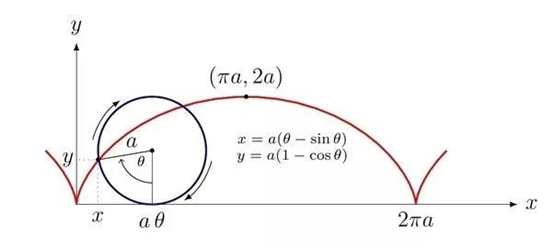
旋轮线的历史

旋轮线有时候会由于其在数学家当中挑起很多纷争而被称为“几何学家的海伦”，纷争之一便是谁发现了这个形状。

最早的候选者之一是给毕达哥拉斯写传记的人伊安布利霍斯（Iamblichus，公元前245-公元前325年），其他的候选者还有包括德国的尼古拉斯-库萨（Nicholas of Cusa，公元1401-1464）、法国人Charles de Bovelles（1475-1566），意大利人伽利略（Galileo Galilei，1564-1642）、法国人马林·梅森（Marin Mersenne，1588-1648）等等一众博学的人。但没人能肯定谁才是最先发现旋轮线的人。

伽利略是最早研究旋轮线并给它起名的人，他甚至用金属板制作了旋轮线的模型来研究旋轮线下的面积。如果那时候有微积分的话或许就容易一些了吧。顺便一提，发明水银气压计的托里拆利（Evangelista Torricelli）才是最终求解单条旋轮线下面积的人。

【一段旋轮线下方的面积恰好是这个圆的面积的三倍。在没有微积分的时代，计算曲线下方的面积几乎是一件不可能完成的任务。伽利略在试遍了各种数学方法却都以失败告终之后，伽利略果断地耍起了流氓，用物理实验的方法测出了图形的面积，他在金属板上切出旋轮线的形状，拿到秤上称了称，发现重量正好是对应的圆形金属片的三倍。用物理实验解决数学问题也不是一件稀罕事了，广义费马点（generalized Fermat point）问题就能用一套并不复杂的力学系统解出，施泰纳问题（Steiner tree problem）也可以用肥皂膜实验瞬间秒杀。】

随着时间推移，旋轮线吸引了大批有名望的数学家，其中包括笛卡尔、费马、帕斯卡、牛顿、莱布尼茨、洛必达、伯努利、欧拉、拉格朗日等等。他们显然很喜欢创造一些关于旋轮线的竞赛和问题，之后再以相互攻击和辱骂结束。帕斯卡（Blaise Pascal）早先就创造了一个关于求解旋轮线的重心、面积以及体积的比赛，并以西班牙金币作为奖金。可惜，三位评审认为没有人获胜。伦敦的圣保罗大教堂的设计者克里斯托弗·雷恩（Christopher Wren，1632-1723）递交了一份关于计算旋轮线长度的证明，虽然这不是竞赛的内容，但仍值得赞许。一位评委在多年后声称自己已经解决了这个问题但一直没有文字记载，于是引发了舆论战争。（起码雷恩通过了自己发表的成果获得了属于他的声誉。）遗憾的是，伯努利（Johann Bernoulli）在1696年提出的挑战最终也以失败告终。伯努利在1696年向顶尖数学家们提出了他的问题：

我，约翰·伯努利，致全世界最聪慧的数学家们：

对于聪明的人们来说，没有什么比一个直白且具有挑战性的问题更具有吸引力的了，更别说这些解法可能会让他们声名鹊起，流芳百世。根据帕斯卡、费马等人提出的例子，我希望我也能通过提出一个现在最顶尖的数学家们考验自己头脑的技巧和力量的问题，来获得学界的感谢。如果有人能够给出我接下来的问题的解法，那么我将在公众面前表达对他的赞美。

在一个垂直空间中有点 A 和点 B ，有一质点只受到重力的作用从 A 至 B ，它的轨迹经过什么样的曲线用时最短？

伯努利给公众了六个月的时间去提交解答，但没有收到回应。莱布尼茨提议将提交的期限延长至一年半，在这个延长期里，牛顿完成了这个挑战。

约翰·伯努利宣称自己有一个漂亮的解法，但暂时不公布，看看有没有聪明人能解出来。他想向欧洲数学界表明，自己才是最聪明的，尤其是比哥哥雅各布·伯努利聪明。当时约翰·伯努利总共找到了两种解法(现在一般称为“直接法”和“间接法”)，根据莱布尼茨的建议，他最初只发表了“间接法”(即“费马原理”解释)，然而最后一步的解释却有误。直到1718年他才公开他的“直接法”(这也是唯一从曲率方向解释的方法)。但是在变分法的初创时期，像最速降线这类变分问题什么是完整解答往往是含糊不清的。后来经过Euler，Legendre，Jacobi和Weierstrass等人进一步研究最速降线等变分问题的必要性和充分性，变分法的理论基础进一步完善了。

据牛顿说，他是在1697年1月29日下午4:00从皇家铸币厂回家时收到的约翰·伯努利的信件的。他工作了整晚并在第二天以匿名的方式邮出了自己的正确解答，但由于这个解答太过于优秀、太过于“牛顿”，伯努利一下子就认出了“留下这个爪印的狮子”。牛顿一晚上的解决时间打破了伯努利所用的两周的记录。牛顿在自己的信中加入了一些当时数学家爱表达的不屑：“我不喜欢被外国人在数学方面纠缠和取乐……”牛顿从来都不怎么讨人喜欢，可以说是不近人情。

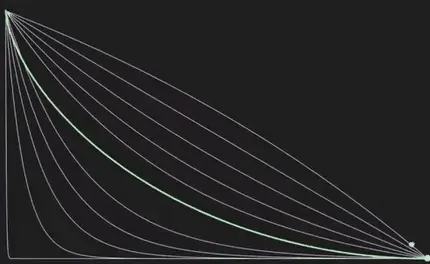
这个牛顿和伯努利解出的最快路径被称为最速降落曲线（brachistochrone curve），来源于希腊语中的“最短时间”，根据这篇文章的主题相信大家也猜到了，这个路径就是旋轮线的一段，下面的动图用实验来展示这个问题：

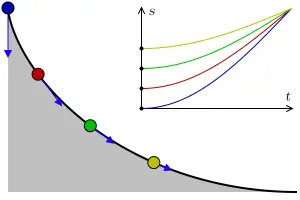
关于旋轮线的另一个插曲是等时降落曲线（tautochrone curve），来源于希腊语“同样时间”，你可以把一个小球放到这个曲线的任意位置，到达最低点所用的时间都是相等的。这个图形来源于半条旋轮线，下面这个动图展示了这个曲线：

还有一个叫旋轮线摆的东西，这个摆的顶端在两条旋轮线的交点位置。这个摆的线会沿着两个旋轮线弯曲，而这个摆扫过的线居然是另外一条旋轮线！