前馈神经网络 FNN

• 首先我们介绍前馈神经网络的基本结构。

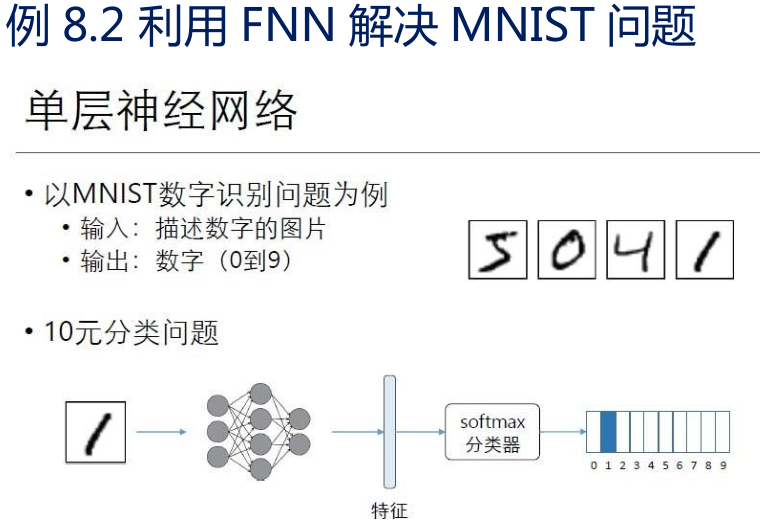
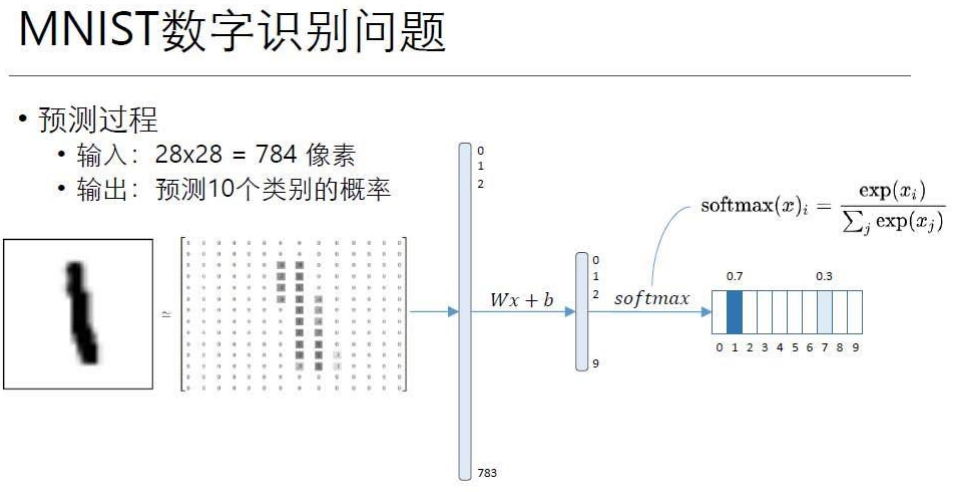
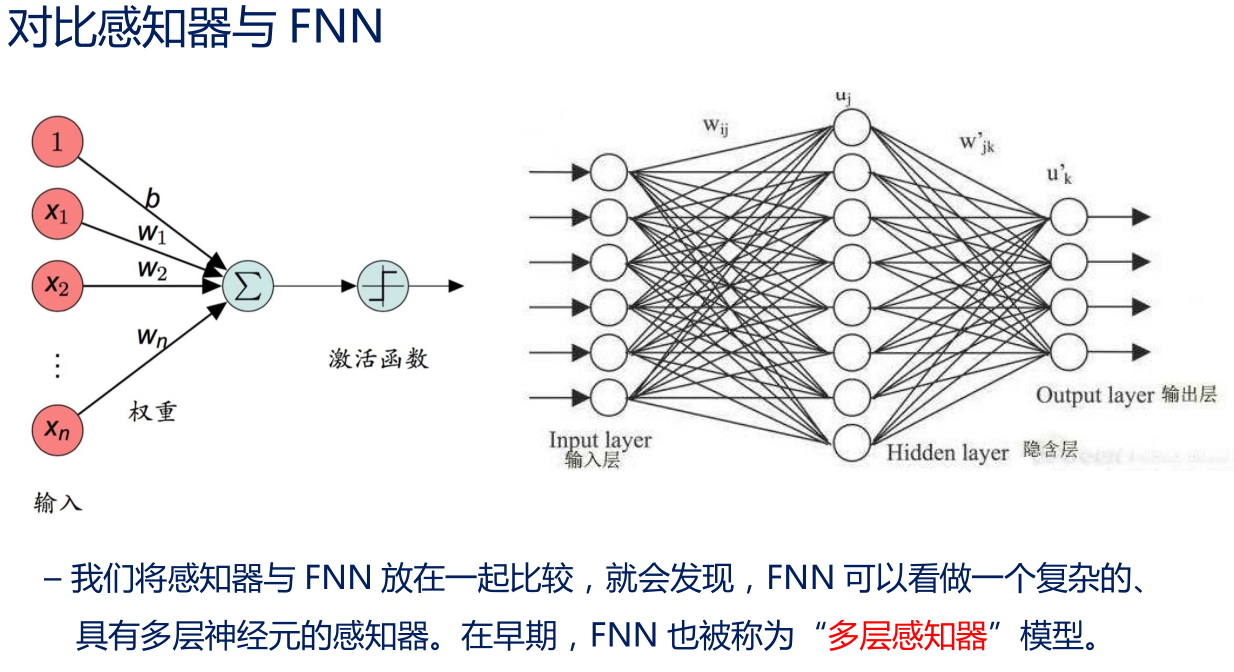
• 如图所示，一个标准的前馈神经网络包括：

• 1 个输入层、

• 1 个或多个隐含层、

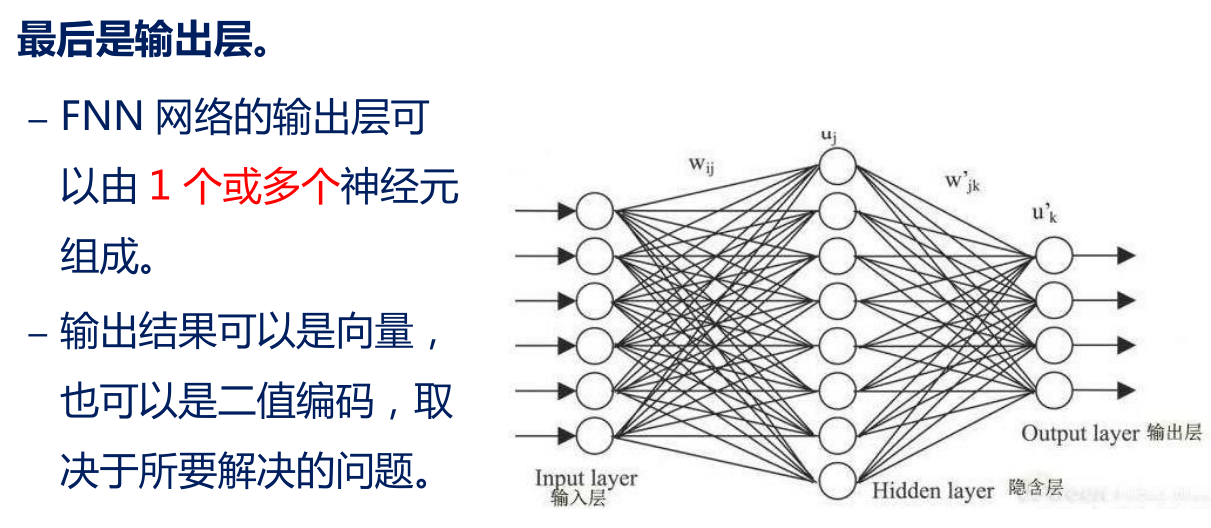
• 1 个输出层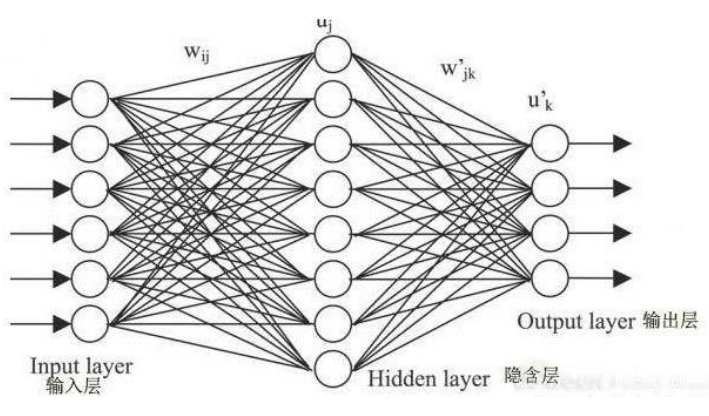

• 输入层之后，连接有若干个隐含层。

– 所谓隐含层，是指其中神经元的状态在输出端无法直接观测，看起来是“隐藏”的。

– 在 FNN 中，隐含层均为标准神经元，带有 sigmoid 激活函数，其输入的权重需要学习得到。

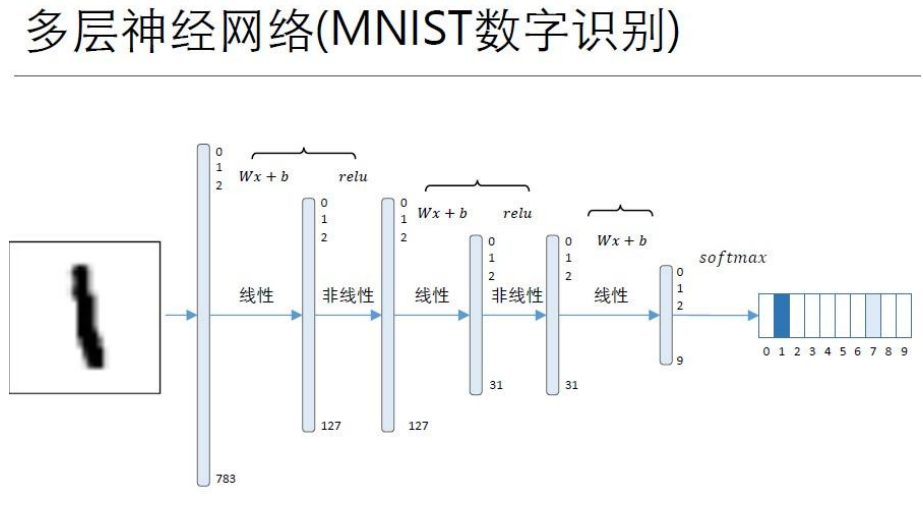
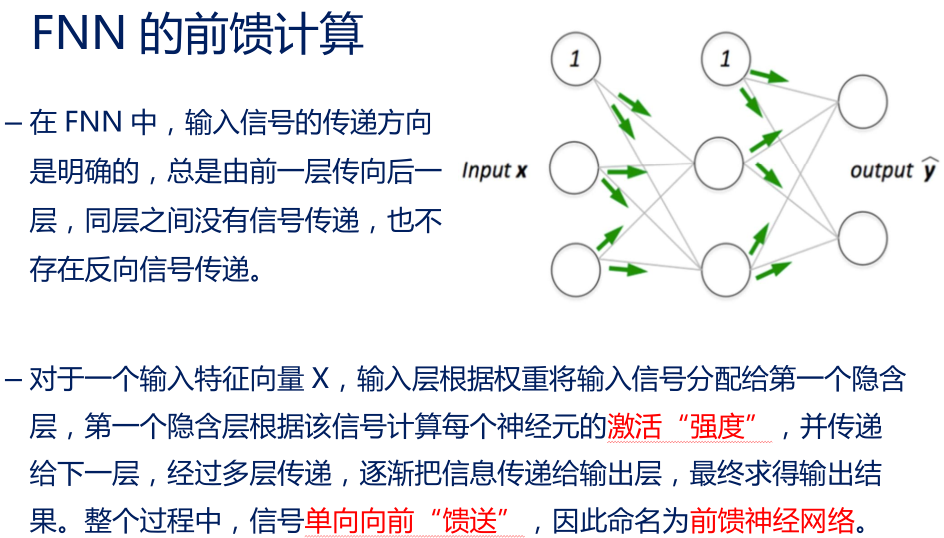
– 输入层与隐含层、两个隐含层之间的所有神经元均存在连接，即，后一层每个神经元接受到的输入信号为前一层所有神经元的输出加权和，又称为全连接。

– 但同层神经元之间不存在连接。这样保证了信息可以逐层向下传递。前馈网络也由此得名。

FNN 的学习问题

• FNN 具有多层神经元，权重的调整具有 3 个难点：

– 网络误差是由多层信号累积导致，如何“分配”误差到各个层？

– 隐含层神经元无法直接观测其误差，如何调整权重？

– 全连接层权重数量众多，计算量问题凸显。

• 由于这些问题，在神经网络发展的前 20 年，多层神经网络一直认为不可行，直到“错误反向传播（BP）算法”被提出。

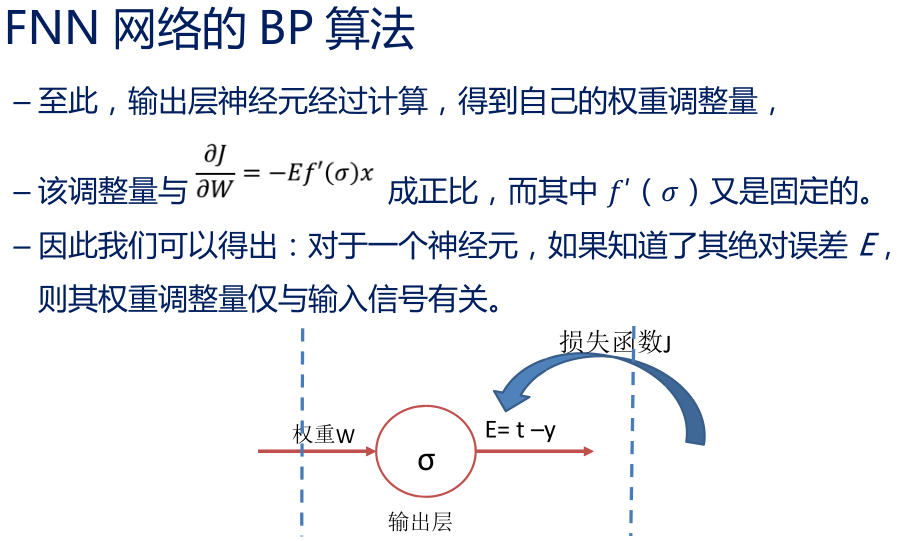
误差反向传播算法（BP）

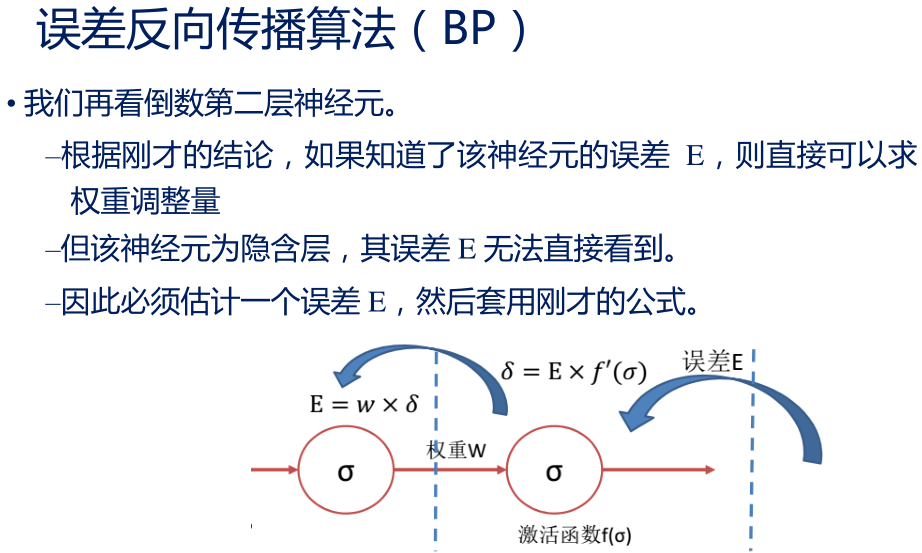
• 对隐含层神经元 误差 E 的估计，就成了 BP 算法的核心

• BP 算法将输出层的 E╳ ′（ ）信号定义为 δ，然后令 δ╳W 作为倒数第二层神经元的 误差信号 E

• 有了这个估计的 E，BP 算法就可以根据刚才的计算方式，计算隐含层神经元的权重调整量。而且，在计算过程中，还可以继续算出当前层的 δ 信号，将误差继续向前一层传播。

• 这就是误差的“反向传播”

–综合起来，所谓的误差反向传播，其实就是从输出层开始，逐层计算 δ 信号，调整自身权重，并且将 δ 信号传向前一层。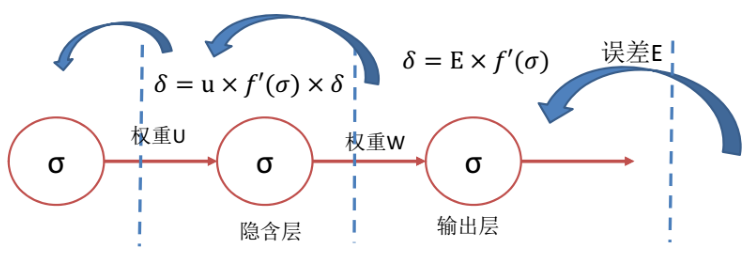

– 对于每层有多个神经元的情况，可以认为，输出层在“看到”了误差信号之后，将该误差按照权重比例“反传”给上一层神经元

– 上一层神经元则按照权重接收反传的若干误差信号，汇总形成自己的误差信号，并再度反传。

• 至此，我们可以训练多层神经网络了。

• 训练过程可以分为以下步骤：

 前馈计算：从输入层开始，计算每一层的状态和激活值，直到最后一层；

 误差计算：计算当前实例产生的误差

 误差反传：从输出层开始，逐层计算每个神经元的 信号，并反向传播到前层

 权重更新：根据 信号，计算权重的导数，并更新参数。

BP 算法的梯度弥散问题

BP 算法对多层网络的训练提供了完整的方法，但是当时使用的sigmoid 激活函数很容易遇到 “梯度弥散”问题：

– 随着神经元网络层数增加，神经元很容易落入“饱和区域”，此时神经元输入倾向于 0 或者 1，其导数则接近 0 点。

– 此时做误差反向传播，会发现导数值非常小，误差信号几乎不可能传递到 3 层以上的网络。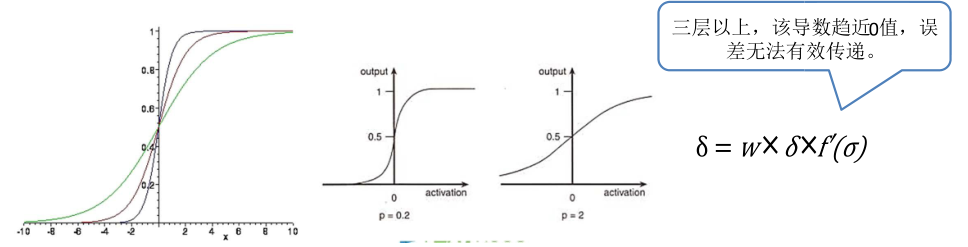

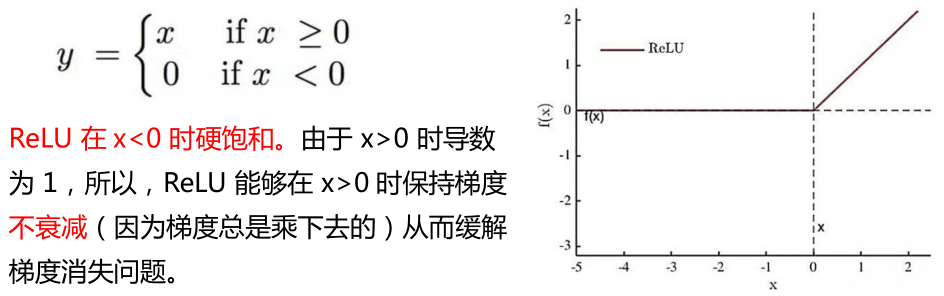
新型激活函数 ReLU

• 直到 2010 年，Hinton 提出了新型激活函数 ReLU。