辅导功课 VS 监督学习

• 要有许多习题集                                    • 要有许多“样本”

• 要有答案 • 每个样本要有明确“答案”    • 犯错会被“吼” • 犯错会被“惩罚”

• 多次练习直至不再犯错                          • 多次练习直至不再犯错

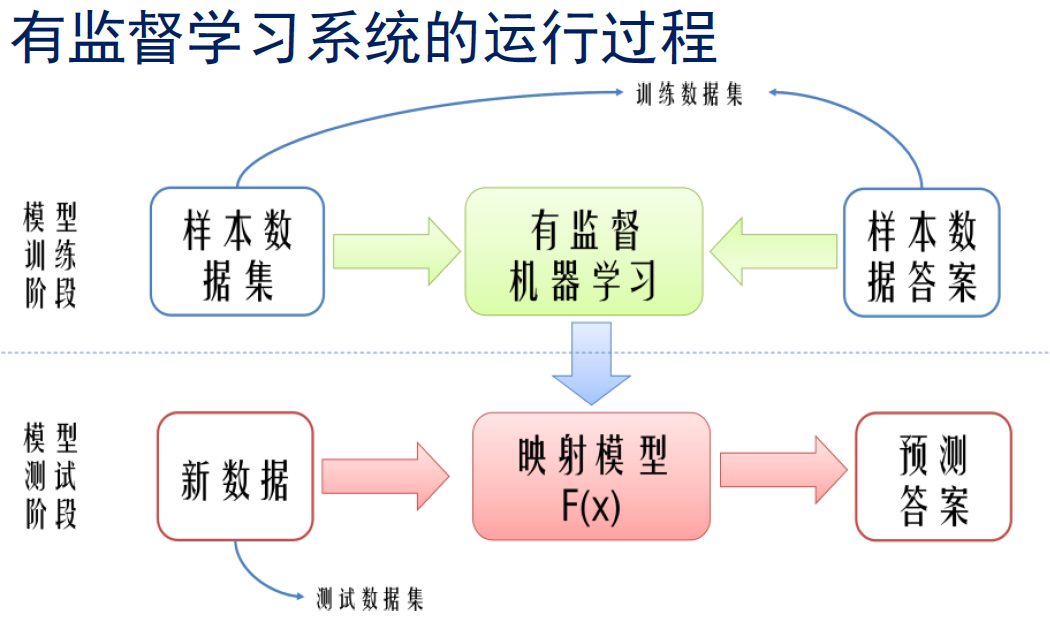
 有监督机器学习的基本框架

 有监督机器学习的典型方法

K近邻算法

决策树算法

支持向量机

有监督机器学习的数学描述

– 给定一些训练样本:{(xi,yi), 1<i<N};

– 其中xi 是输入，yi 是需要预测的目标，

– 计算机自动寻找一个决策函数f(·) 来建立x 和y 之间的关系：

yˆ = f (φ(x),θ)，

其中：φ是一种函数变换，θ是模型参数

– 选取参数 θ 使得 yˆ 与预测目标 y 之间的差别尽可能小

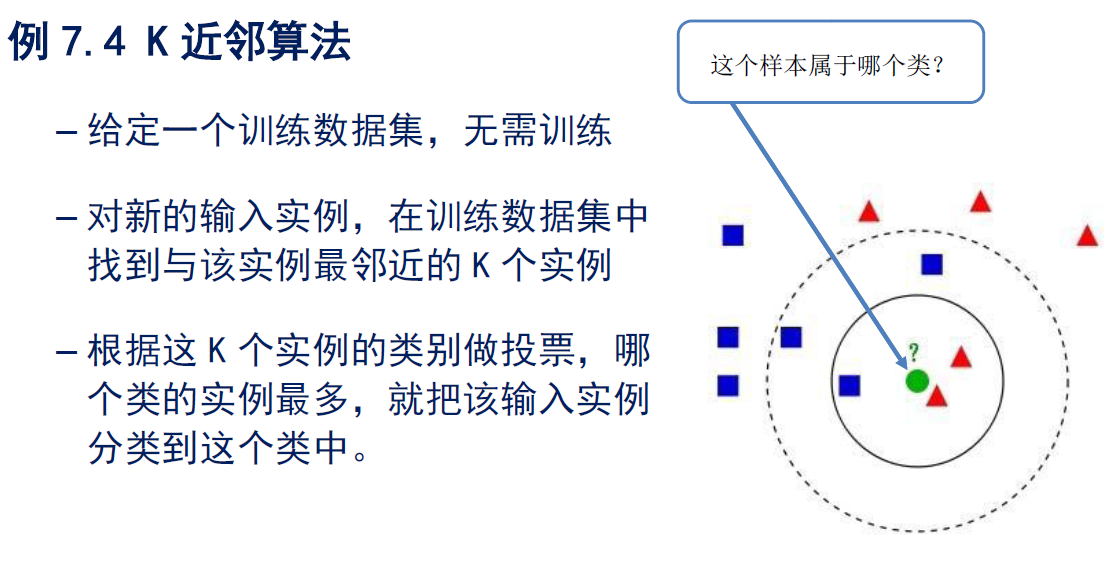
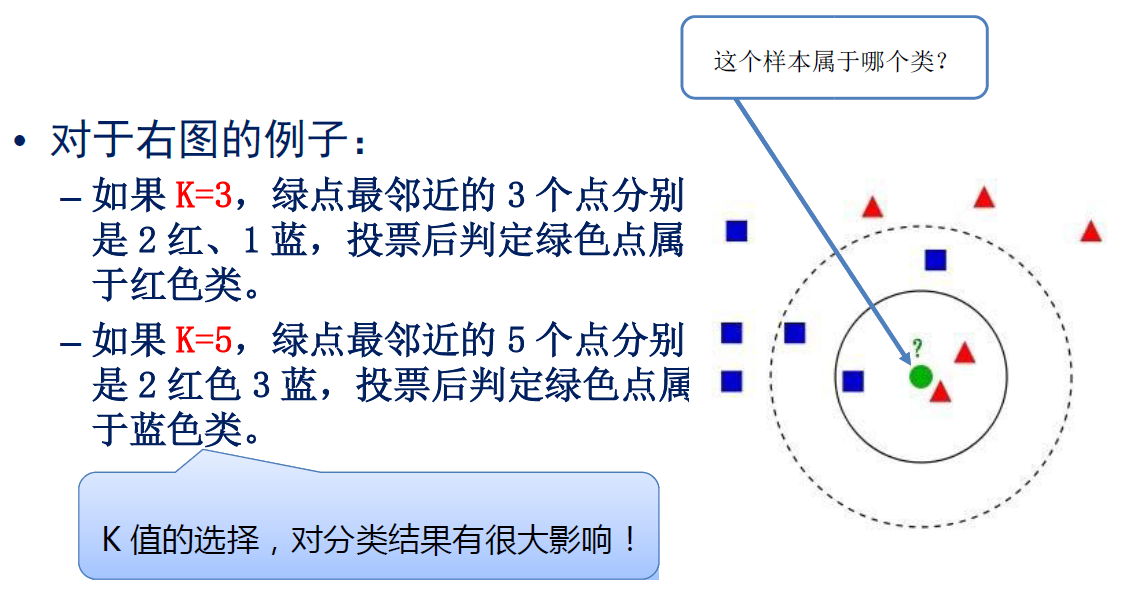
例7.5 决策树算法

• 很多情况下我们的样本是下面这样的表格统计数据。

• 如何从中归纳出规律？如何根据新的数据快速判断结论？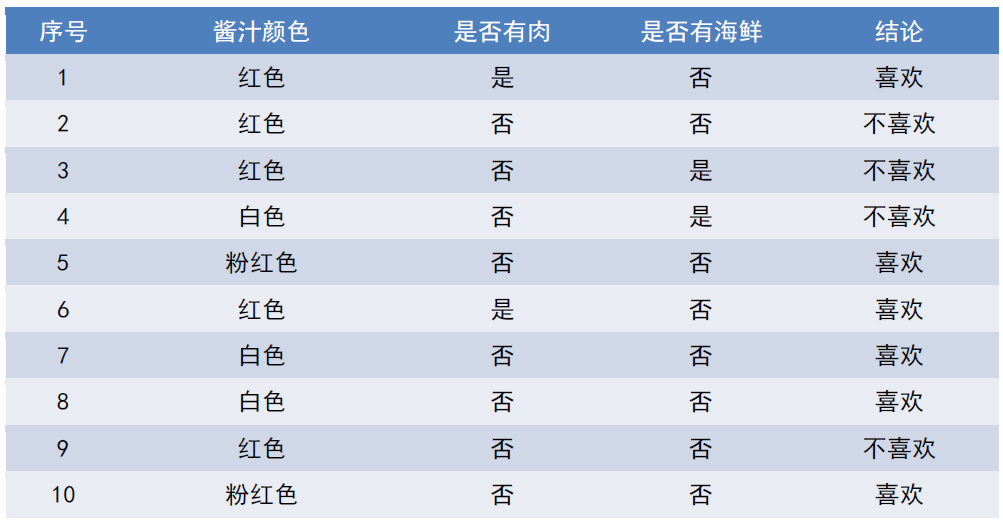 

规则归纳问题，适合用决策树来表示，如意大利面决策树。

• 关键问题是：如何从表格构建出这样的决策树？

• 换言之：如何选择各个属性决策的顺序？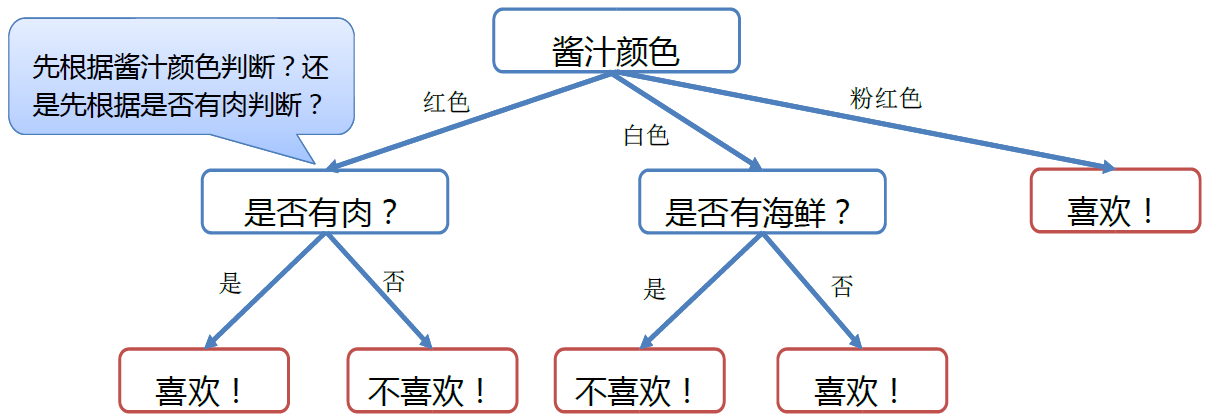

ID3 算法，昆兰（Quinlan，1986）

• 算法思想：

– 属性在决策树中的位置不同，决策树的效率是不同的。

– 如果一个属性对于所有样本都没有区分能力（比如有是否能吃这个属性），那么对于决策毫无用处。

– 如果一个属性恰好能将样本数据一分为二，则这是一个好的属性，应该尽量在决策早期就使用。

– 如果根据一个属性做判断，样本仍然有若干种情况，则该属性不应该出现在决策早期。

– 昆兰提出利用“信息增益”来对属性进行排序。

– 如果一个属性执行后，使得数据集上的信息增益最大（最有序），则该属性应该优先被执行（更接近根节点）。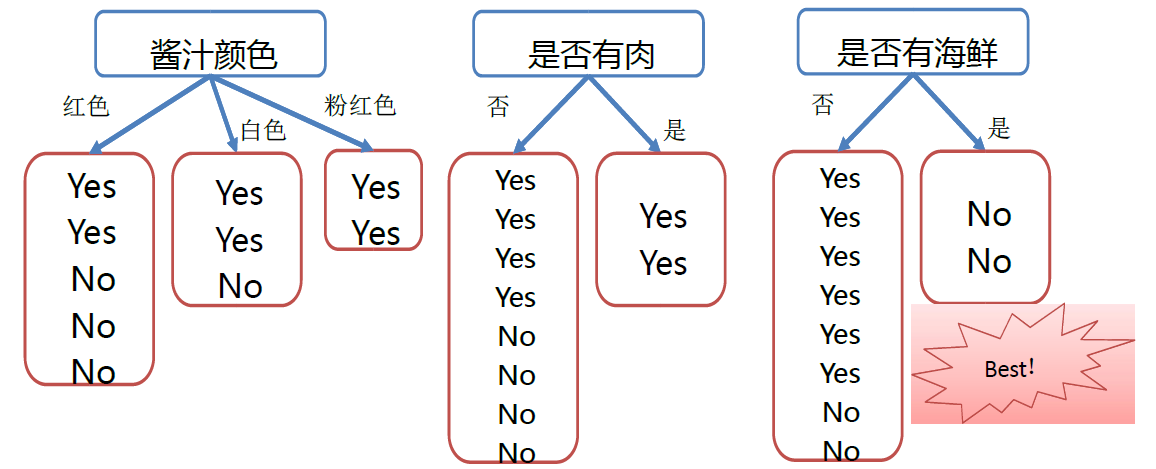

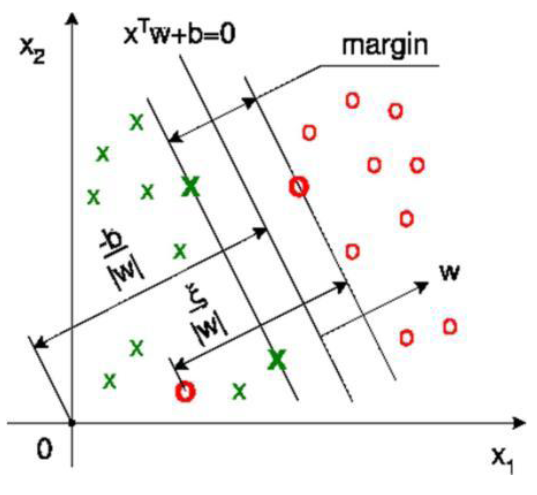
例7.6 支持向量机模型（SVM）

–1967年，俄罗斯数学家Vapnik等人提出最大间隔超平面的思想

–1992年，Boser将核方法应用于最大间隔超平面

–1995年，Corinna Cortes和Vapnik 提出使用“软间隔”思想

–机器学习领域大名鼎鼎，直接导致

2000年代统计机器学习的繁荣。

基本思想

– 对于二分类问题，将样本数据表示为空间中的点。

– 使用“平面”来切割空间，实现分类。

– 如何选择“平面”，成为关键问题。

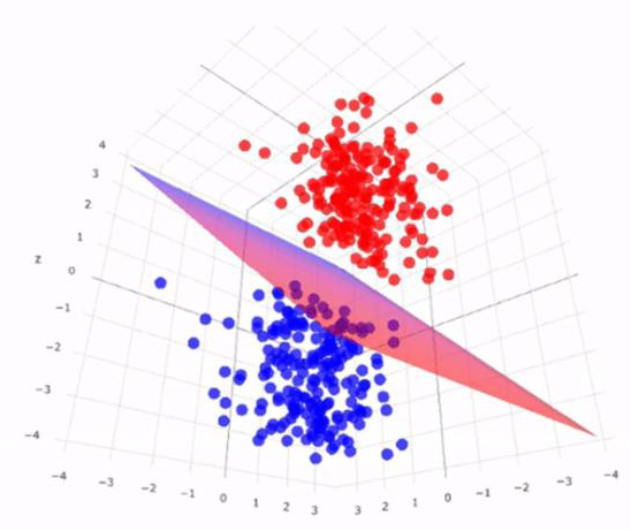
我们认为，一个样本点与分割平面的距离越远，则分类越明确。

– 如果我们能找到一个平面，使得在其两侧，两类样本之间的间隔尽可能大，则该平面就是优秀的分割平面。

– 为达到间隔最大的目标，只需要看距离平面最近的几个样本，它们代表着间隔。称为“支持向量”。