蚁群算法(Ant colony optimization, AOC)

• 由意大利科学家Marco Dorigo等人于1991年提出，其灵感来源于蚁群在觅食过程中，总能找到蚁穴到食物之

间最短路径的现象。

• 我们在生活中也经常能遇到类似的情况

 一群蚂蚁看似在“乱走”

 一旦遇到食物（糖），很快就能看到蚂蚁排起队来去吃糖

蚂蚁是怎么找到这条路的呢？

蚂蚁觅食

• 学者们很早就对蚁群觅食行为进行了生物学研究，发现许多有意思的现象：

– 蚂蚁“智能”程度非常低，单个蚂蚁的觅食路线具有很大随机性

– 蚂蚁在外出觅食路上，会沿途释放一种化学物质“信息素”

– 蚂蚁在遇到多条道路选择时，会根据路径上信息素的浓度来选择道路。信息素浓度高的道路具有更多选择概率。

– 信息素会随着经过路线蚂蚁数量提高而增加，也会随着时间推移逐渐消散。

• 就是这样的简单原则，使得大量蚂蚁整体表现出优秀的

“寻路”能力。

蚁群算法：模拟蚂蚁觅食

• Dorigo等人受到蚂蚁觅食现象启发，建立其抽象框架，形成蚁群算法。这种算法特别适合于解答“从A点出发到达B 点最短路径”问题。尤其是，当A和B为同一点时，其实就是我们第五章中所介绍的“旅行商问题”。

• 蚁群算法也是从生物智能现象中抽象出算法的典范。我们来看蚁群算法是如何进行算法抽象的。

建立蚁群算法

• 要模拟蚁群觅食，我们得做四个方面的抽象。

 如何模拟蚂蚁，以及其行为；

 如何模拟蚂蚁觅食的环境；

 如何模拟蚂蚁选择路线的行为；

 如何模拟蚂蚁释放信息素、信息素消散的现象

我们依次来看。

（1）模拟蚂蚁

• 蚁群算法中，蚂蚁是最基本单位，我们不妨称为“人工蚂蚁”。

人工蚂蚁应该具有下面的特点：

– 每只蚂蚁都有相同的目标，以相同速度运动。

– 蚂蚁在行走过程中，在达到目的地前，不走回头路，不转圈。

– 每只蚂蚁都根据相同的原则释放信息素、选择路径。

– 每只蚂蚁都记得自己经历路径的长度和过程。

– 种群中蚂蚁的数量不会发生变化，用 m 表示。

（2）模拟环境：“地图”

• 我们将蚂蚁觅食的环境抽象成“具有N个节点的全连通图”

– 图上一共有 n 个节点；

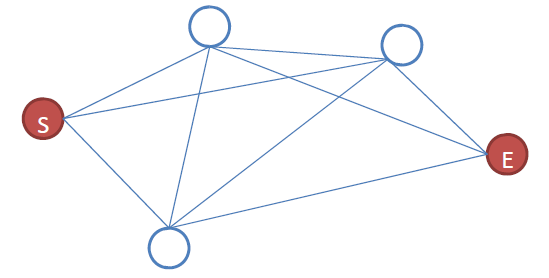
– 每个节点都与其他所有节点直接相连，任意两点x，y之间的距离记为 dxy 均为已知（这一点与真实蚂蚁不同！）；

– 具有明确的起点和终点。

如图，有5个节点

S为起点，E为终点

蚂蚁总是从起点S出发，到达终点E即结束。

(3) 模拟蚂蚁选择路线

– 有了人工蚂蚁和地图，下面我们来设想蚂蚁如何选择路线。我们用例子来说明。

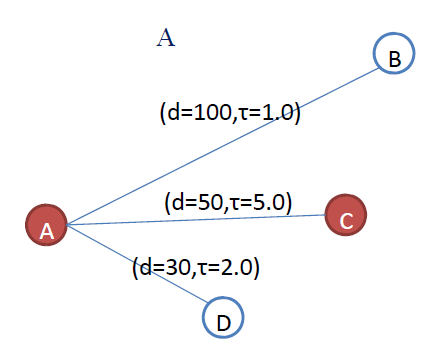
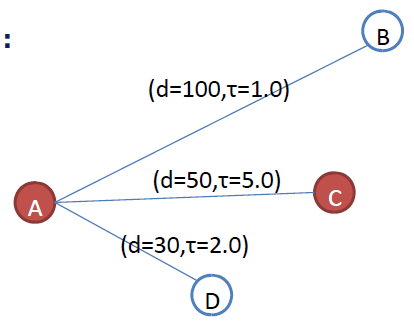
• 假设蚂蚁现在处于A点，下一步有B、C、D三种路线选择。

– 已知路线距离分别为dAB=100、dAC=50、dAD=30。

– 已知路线上的“信息素”τAB=1.0， τAC=5.0， τ =2.0。

那么，蚂蚁应该如何选择路线？

• 第一种情况，我们先不考虑信息素的影响，此时：

– 人工蚂蚁仅仅知道从A点出发到其余各点的距离

– 则蚂蚁应该从经济性角度出发，选择距离 短的路线行动。

– 符合我们之前介绍过的“贪心原则”

• 第二种情况，我们不考虑各点间的距离，此时：

– 蚂蚁应该选择“信息素”值 大的路线行动

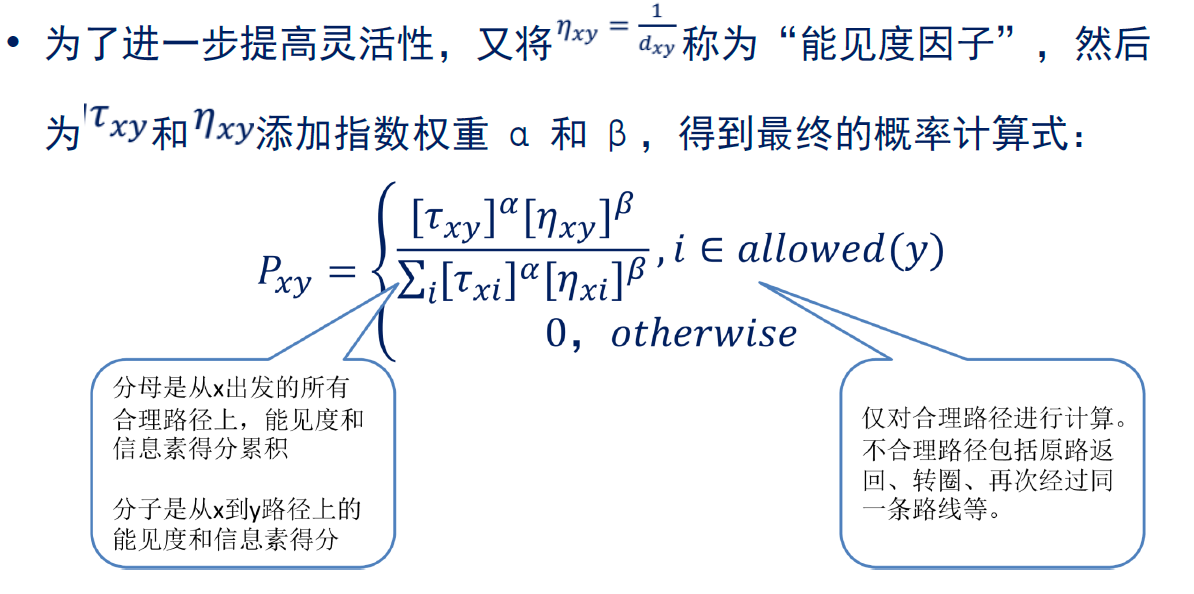
• 由于蚂蚁智力有限，上面的准则应该概率化，有：

– 蚂蚁选择路线的概率，与该路线的长度成反比，路线越短，选择概率越高

– 蚂蚁选择路线的概率，与该路线上信息素浓度成正比，信息素越高，选择概率越高

（4）模拟信息素释放和消散

 在实际中，每个蚂蚁独立行动，边运动边释放信息素，同时信息素随着时间推移而消散。整个过程与时间相关。

 我们可以在系统中添加真实时间如秒、分钟等，来精确模拟每个蚂蚁在一定时间段中的行为。但由于我们研究的是蚁群整体，因此这种精细模拟并非必要。

 一种常见的策略，是将时间“片段化”，以“cycle”为单位来模拟时间。

–一个cycle表示蚁群中所有蚂蚁均从出发点成功达到目标点。

–信息素在一个cycle结束之后统一更新，不考虑cycle期间信息素的消散和累积。

• 这种假设称为“蚁圈模型”。

– 蚁圈模型中，我们以cycle为时间单位，每个cycle结束后，时间 t 增加1。

– 为了模拟信息素的消散，我们简单认为信息素随时间以一定比例逐渐消散，这个比例设计成“信息素保持系数” ρ ，有0<ρ<1。

• 如，对于路径xy而言，如果没有蚂蚁经过，则：

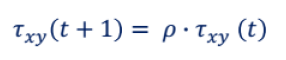
由于ρ<1，因此如果xy路径始终没有蚂蚁经过，则该路径上的信息素会逐渐减少，直至消散为零。

• 对于一只蚂蚁，在一个cycle结束之后，其经过的路径是可以记录的。

• 我们认为，找到比较好的路线的蚂蚁，应该很“优秀”，因此它留下的信息素更有价值。也就是说，如果蚂蚁 k 找到的路线越短，那么沿途留下的信息素应该越多。

• 因此，如果 k 经过了 xy ，那它留下的信息素就是：

、

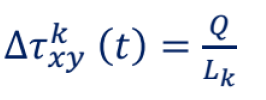• 其中，Q为常数，Lk就是蚂蚁k在当前cycle中找到的路径的总长度。

• 至此，我们完全实现了蚁群算法的四个模拟问题

– （1）如何模拟蚂蚁，以及其行为；

– （2）如何模拟蚂蚁觅食的环境；

– （3）如何模拟蚂蚁选择路线的行为；

– （4）如何模拟蚂蚁释放信息素、信息素消散的现象

– 由此，我们可以建立蚁群算法的全貌

蚁群算法实施步骤

• Step1：初始化蚁群数量、各个系数、初始化地图，地图中所有路径信息素为0

• Step2：启动cycle，在出发点放置所有蚂蚁，按照概率行动

• Step3：等待所有蚂蚁到达终点，根据路径，更新信息素

• Step4：如果没有达到停止条件，重复step2，启动下一个cycle

• Step5：如果达到停止条件，选出最优秀的蚂蚁对应的路线，即为答案。

以下是，蚁群算法的程序运行演示：