新达尔文主义

• 新达尔文主义并不是由达尔文一个人提出的，而是包括了：

– 达尔文的进化论

– 门德尔的遗传学理论

– 魏斯曼的自然选择理论

新达尔文主义

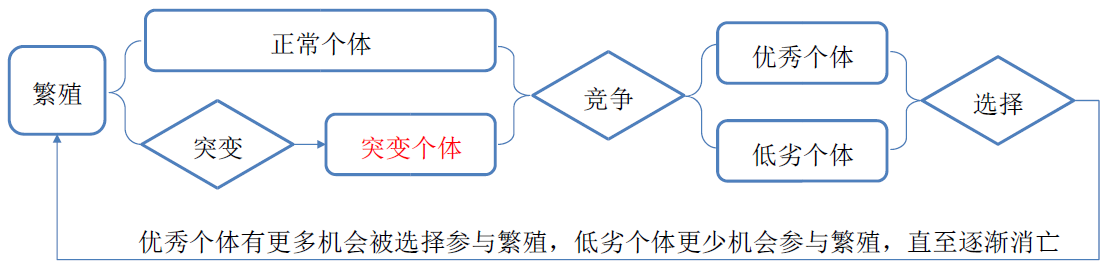
• 新达尔文主义认为，生物进化包括四个过程：

– 繁殖：物种代际延续的基础

– 突变：物种适应不断变化环境的关键

– 竞争、选择：物种优胜劣汰、不断优化的关键

• 这四个过程可以用一个封闭的循环图来描述

遗传算法基本思想

• 进化智能算法的目标，就是用计算机来模拟进化过程，从而求解问题。最简单的进化算法，是由进化智能创始人之一的John Holland于1975年提出的遗传算法（GA），该算法在1989年经Goldberg汇总改进，形成完整的框架。

• 为了实现对进化论的模拟，遗传算法必须考虑以下几方面问题：

– 什么是物种？什么是物种的生存环境？

– 如何模拟物种的“繁殖”，产生下一代正常个体？

– 如何模拟物种的“突变”， 产生下一代的突变个体？

– 如何评价每个个体的优劣，从而模拟“竞争与选择”？

• 我们逐一来讨论

Q1：什么是物种？

– 在遗传算法中，我们要求解的问题就是“物种”。求解问题的每个可能的解，或者中间状态，都可以设计为该物种的“个体”。

– 那物种如何表示呢？在现实世界中，区别生物个体性状由基因决定，个体的全部基因构成“染色体”。

– 遗传算法借鉴了基因的思想：用符号串表示基因，若干基因构成染色体表示个体。

– 简单的染色体就是一串二进制数，其中的每个“位”就是基因。

 1 0 1 1 0 1 0 0 0 0 1 0 1 0 1 0

– 染色体与我们第五章介绍的“状态向量”有类似之处。

Q2：什么是物种的生存环境？

– 有了物种之后，我们还要规定物种生存的环境。

– 环境设计包括：

• 规定物种生存的限制条件。

• 规定物种适应环境的能力的指标，一般是量化指标。

– 环境设计要保证最优解对应的个体具有最强的适应能力，最优解个体的“基因”有更高的概率在代际传递和保持。

– 环境的设计与具体问题息息相关，我们稍后通过具体例子来说明。

Q3:如何模拟物种的“繁殖”

– 好，现在我们已经模拟出物种和环境了，下面要模拟物种的繁殖。

– 首先，我们从“基因”传承的角度来看繁殖过程。假设有两个个体X和Y结合产生后代，则繁殖的过程就是：X和Y分别随机拿出一半基因，组合形成新个体的基因。

– 比如，X的基因为AA’, Y的基因为BB’，则后代的基因组合可能是： AB，AB’, A’B， A’B’四种之一。

– 这就是“基因交叉”原则。

• 对于遗传算法来说，我们同样有“基因”，因此遗传算法中的繁殖，也可以通过基因交叉来实现。

– 从种群中选择两个个体；

– 随机确定一个染色体的“断裂点”，注意不是均分。

– 按照一定概率，交叉双亲的染色体生成新的个体。

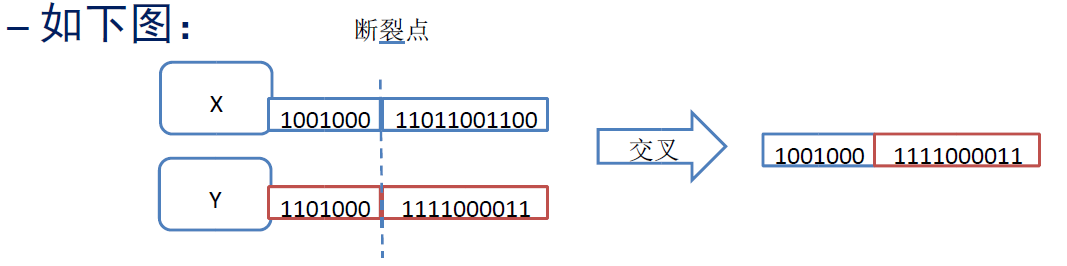
• 交叉基因的概率，称为遗传算法中的“交叉算子”

讲到这里，细心的同学会发现，遗传算法个体的繁殖过程，实际上实现了我们之前所介绍的“状态转移”！

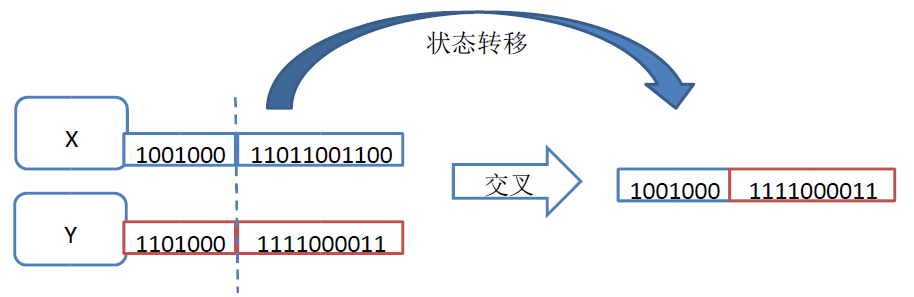
在状态空间搜索中，状态通过转移来实现搜索优化，在遗传算法中，状态转移的过程，就变成了“繁殖”。

– 繁殖过程的“基因交叉”实现了生物基因信息的“传递”。通过繁殖，优秀的基因可以在种群中不断复制、代代相传。

– 但基因交叉不会给物种基因库增加新的“信息”。也就是说，如果环境发生变化，现有基因无法适应，则种群理论上就无法适应这种环境了。

– 在现实中，生物基因存在小概率的“突变”，使得整个种群的基因能够跳跃性变化，从而从大量变化中产生能够适应新环境的基因。

Q4：如何模拟基因“突变”？

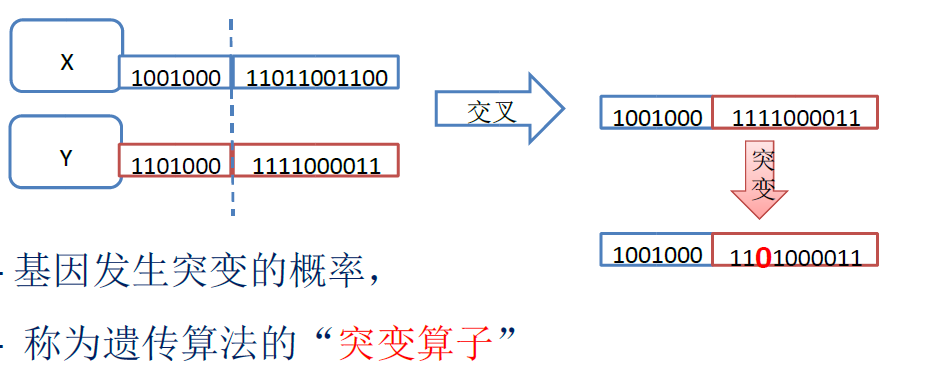
– 遗产算法同样模拟基因的突变过程。

– 在实现基因交叉之后，产生的新的个体中的每个基因，都以小概率发生“突变”，从而产生具有全新基因的后代。

Q5：如何模拟“竞争与选择”？

• 竞争：

– 遗传算法遵循自然界中的优胜劣汰原则，这就需要评价每个个体的适应能力。一般通过设计“适应度”函数来实现。适应度高的个体，更接近问题的 优解。

• 选择：

– 选择就是挑选优秀个体参与繁殖，产生下一代的过程。因此，个体被选择的概率，与其适应度成正比。

– 个体被选择参与繁殖的概率，称为遗传算法的“选择算子”

遗传算法全貌

• 将上面各个思想“组装”成完整的闭环流程，就是遗传算法。算法初始设定阶段:

– Step1：根据求解问题，设计个体染色体表示方式，一般为二进制数字串。

– Step2：随机产生N个个体，作为初始种群。

– Step3：设定交叉概率Pc，突变概率为Pm，选择概率为Ps。

– Step4：设定个体的适应度函数f(x)，计算初始种群中的每个个体的适应度。

• 进化阶段：

– Step5：在当前种群中，根据 Ps概率，选择一对染色体作为“双亲”参与繁殖

– Step6：执行遗传操作：根据Pc 和 Pm概率，对选中的双亲进行基因交叉、突变，生成后代染色体，加入下一代种群中。

– Step7：回到Step5重复繁殖过程，直到下一代种群数量达到N，用新种群（其中均为新一代）替换初始种群。

评价阶段：

– Step8：评价新的种群是否有个体满足停止条件，如为达到要求，则回到Step5继续繁殖下一代。否则停止算法，返回最35优个体。

• 下面我们通过一个实际例子来说明遗传算法的工作过程。

• 求解问题：

– 求函数 f(x)=15x-x2 在x在0～15时的 大值，其中x为整数。

• 我们对应每个步骤来讲解。

Step1：设计染色体

• 题目中x为0～15范围内的整数，取值一共有16种方式。

• 我们只需要4个二进制位就可以表示，因此，染色体对应的就是0000～1111。

Step2～4：初始化

• 我们令

– 初始种群数量 N=6，我们随机产生的0、1串，填充6个染色体对应的所有基因，创建初始种群。

– 交叉概率Pc=0.7 即有70%可能在繁殖时引起交叉

– 突变概率Pm=0.001 每个基因突变的概率

– 选择概率Ps根据种群情况而定，每代不同

– 适应度函数，即我们的目标问题： f(x)=15x-x2

• 根据上面设定，我们随机初始化种群，并且计算个体适应度，如下表：

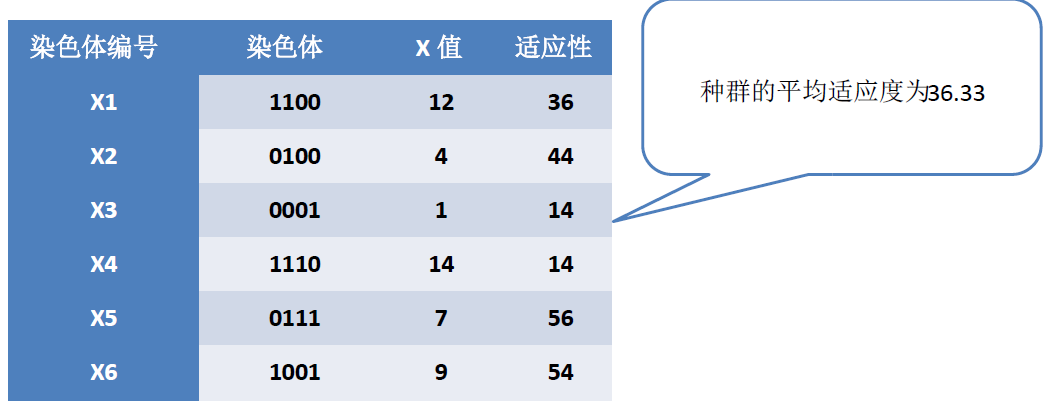
Step5：选择双亲

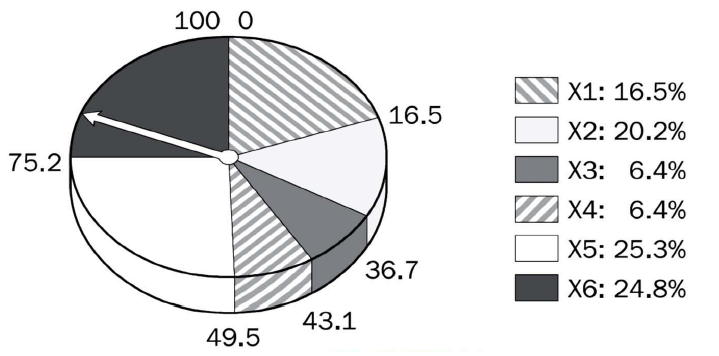
下面根据当前种群的情况，计算每个个体被选择的概率Ps。

– 我们将每个个体的适应度占种群适应度的权重作为概率，如个体X2，其适应度为44，则Ps(X2)=44/(218)=0.202

– 计算所有个体的选择概率，得到选择轮盘，这就是“轮盘选择”：

Step6～7：交叉和突变

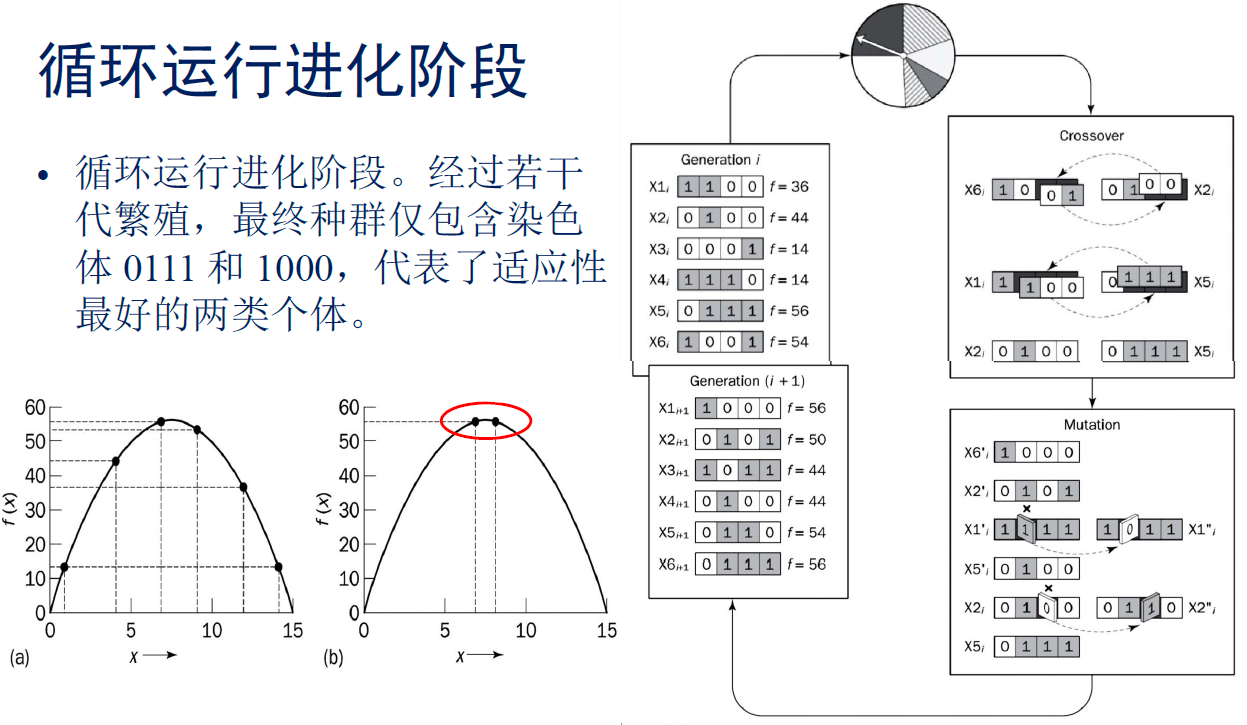
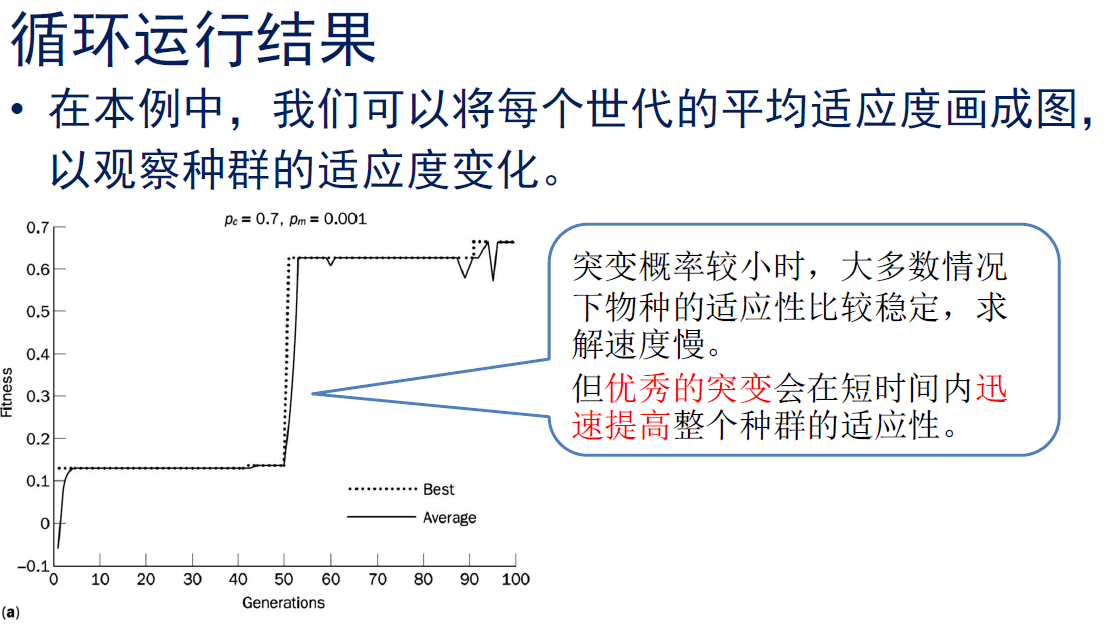
• 本例中我们选择3对双亲，分别为：X6-X2；X1-X5；X2-X5

• 下面对每对染色体，进行交叉和突变。

– 按照Pc=0.7的概率，进行基因交叉。断裂点的选择完全随机。这样，每对染色体在交叉之后，形成一对新的染色体。我们认为这两个新的染色体都有效。

– 然后按照Pm=0.001的概率，对交叉之后的染色体进行突变。得到后的繁殖结果。

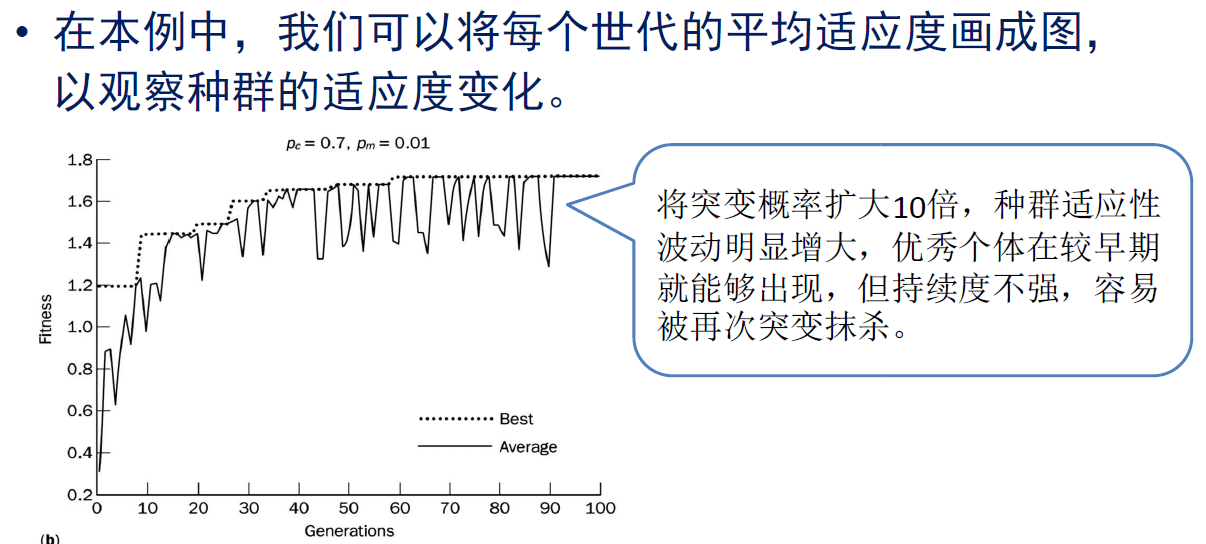
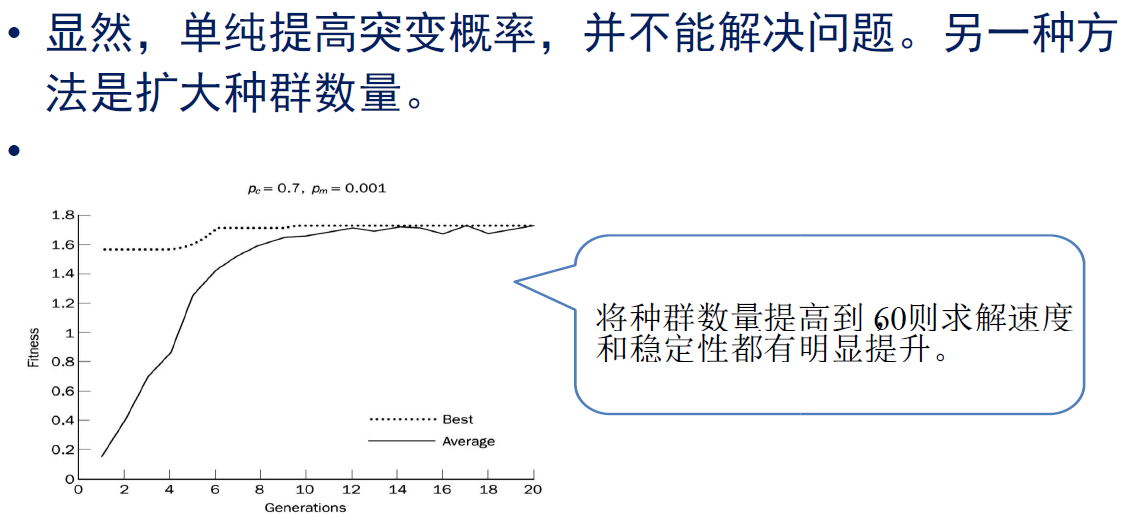
小结：遗传算法与搜索技术

• 至此，我们完整介绍了遗传算法的概念、思想、例子。

• 从形式上来看，遗传算法与我们第五章介绍的状态空间搜索法非常类似。

– 状态表示为向量，类似于状态表示为个体

– 状态转移，类似于个体繁殖

• 在应用中，两种方法略有差别，需要根据实际问题合理选择。

• 状态空间搜索适合于问题清晰，优化目标清晰，容易设想“怎样会更好”，这时设计启发函数，采用状态空间搜索效率很高。如果使用遗传算法，往往效率不佳。

• 但对于一些问题，限制条件非常多，此时设计启发函数很难，因为很难证明所设计的启发函数是A*的，从而无法保证搜索总是有效的。这种情况，使用遗传算法反而更有优势。