博弈搜索：

每个角色在做出决策时，不仅要考虑到自己的立场，还要预测对手可能的反应，由此构成博弈状态空间，在其中进行搜索。

极大极小思路
• 假定对弈只有两方，且双方：
– 都了解并使用同样的对弈规则
– 对弈必有胜负，不存在“双赢、双输”的情况
– 对弈双方都以“最可能赢棋”的目标行动
• 双方的目标的量化：
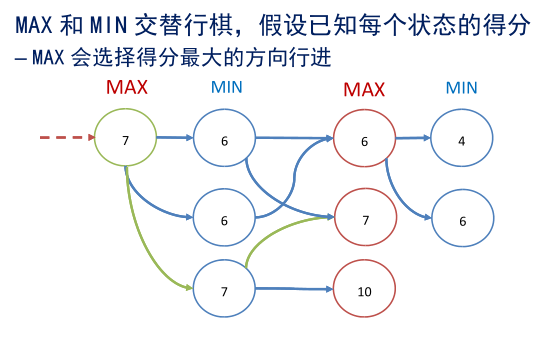
– 我方的目标是使每步得分最大，称为 MAX 方
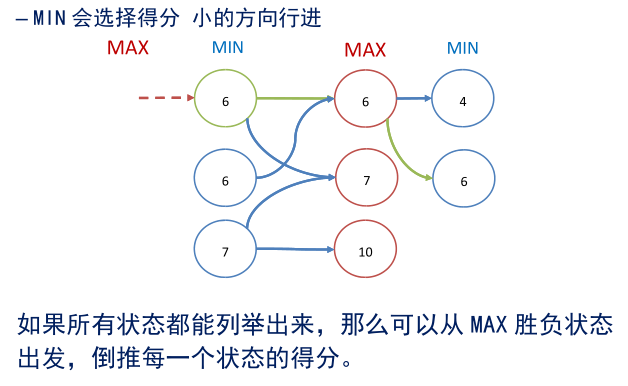
– 对方的目标是最大化他的得分 等价于最小化我方的得分，称为 MIN 方

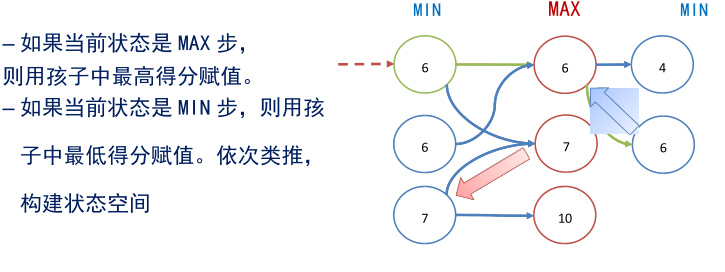极大极小策略的问题
– 极大极小策略要求穷举棋局。在真正的博弈中不可实现。
– 合理的策略是，棋手只考虑向下“若干步”可能出现的棋局，这也是人类棋手在进行对弈时常采用的方法。
– 即固定深度的博弈搜索。

固定深度博弈
• 思想：
– 只在当前 MAX 状态下向下探索固定的层数，如五层；
– 构建出“极大极小”状态子图；
– 转化为状态子图上的极大极小博弈搜索。
• 关键问题：
– 状态子图的“叶结点” 无法得到精确的胜负得分。如何打分？
– 回到启发式搜索：通过设计启发函数，来评估叶结点的启发得分，原理与 A*搜索非常类似。

固定深度博弈
• 使用固定深度博弈搜索的一般步骤：
– （1）在当前 MAX 步情况下，穷举向下 N 步的所有可能棋局。
– （2）在构成的状态子图中，设计启发函数评估每一个叶结点的胜负得分。
– （3）根据叶节点得分，按照极大极小策略倒推每个节点的状态。
– （4）选择当前最优者行动。

α-β 剪枝
• 固定深度的博弈搜索，可以看作是“宽度优先”的，对于复杂棋局如国际象棋，即使只向前看少数几步，可能性也非常多。
• 在人工智能研究早期，麦卡锡就提出了改进方法，采用类似于深度优先的方法构建博弈状态子图，即 α-β 剪枝方法。

从国际象棋到围棋
• 但在围棋领域，由于胜负状态太复杂，无法找到有效的启发方式，即使经过 α-β 剪枝，也很难实现搜索，一直无法突破。
• 2006 年，法国一个团队提出使用“蒙特卡洛树搜索”方式，以“信心上限决策”打分，使计算机围棋能力得到质的提升。为后续方法奠定基础。
• 2013 年，CrazyStone 程序达到人类业余 5 段水平
• 2016 年，Alpha Go 问世，将深度学习、价值网络、蒙特卡洛树搜索技术融合，战胜人类顶尖棋手。