金融数据挖掘

冯国锋

目录

  • 1 Introduction 导论
    • 1.1 What is data mining? 什么是数据挖掘？
    • 1.2 How DM works in financial area？数据挖掘在金融领域是如何应用的？
  • 2 Financial big data 金融大数据
    • 2.1 What is data? 什么是数据？
    • 2.2 Data preprocessing 数据预处理
    • 2.3 Similarity and Dissimilarity of financial data 金融数据的相似性与相异性
  • 3 Decision Tree Classifier with financial applications 决策树分类器与金融应用
    • 3.1 Classification in financial scenario-basic concept and idea 分类算法与金融应用——基本概念与思想
    • 3.2 Introduction to Decision Tree Classifier in Financial Scenario 决策树算法与金融应用——算法介绍
    • 3.3 Methods for expressing attribute test conditions 属性测试条件划分方法
    • 3.4 Measures of impurity in Decision Tree Classifier 决策树分类算法中结点纯度度量方法
    • 3.5 A financial example to compute a Decision Tree 决策树分类器的构建案例
  • 4 Rule-Based Classifier with Financial Applications基于规则的分类器与金融应用
    • 4.1 Introduction to Rule-based Classifier in Financial Scenario 基于规则的分类器与金融应用——算法介绍
    • 4.2 Direct Method for Rule Extraction in Rule-based Classifier 规则提取的直接方法
    • 4.3 An Financial Example to Build Rule-based Classifier 基于规则的分类器的构建案例
  • 5 Naive Bayes Classifier with Financial Applications 朴素贝叶斯分类器与金融应用
    • 5.1 Introduction to Naive Bayes Classifier in Financial Scenario 朴素贝叶斯分类器与金融应用——算法介绍
    • 5.2 A Financial Example to Build Naive Bayes Classifier 朴素贝叶斯分类器的构建案例
  • 6 Bayesian Networks with Financial Applications 贝叶斯网络分类器与金融应用
    • 6.1 Introduction to Bayesian Belief Networks in Financial Scenario 贝叶斯信念网络分类器与金融应用——算法介绍
    • 6.2 A Financial Example of BBN 贝叶斯信念网络分类器案例
  • 7 Financial Classification issues-Underfitting and Overfitting 分类算法在金融应用中的可能问题——拟合不足与过拟合
    • 7.1 Underfitting and Overfitting (1) 拟合不足与过拟合(1)
    • 7.2 Underfitting and Overfitting (2) 拟合不足与过拟合(2)
  • 8 Fiancial Classification Evaluation-Model Evaluation and Comparison 分类算法在金融应用中的结果评估——模型评价与对比
    • 8.1 Fiancial Classification Evaluation-Model Evaluation 分类算法在金融应用中的结果评估——模型结果评价
    • 8.2 Fiancial Classification Evaluation-Model comparison 分类算法在金融应用中的结果评估——模型对比分析
  • 9 Association Analysis with Financial Applications-Apriori Algorithm 关联分析与金融应用——Apriori算法
    • 9.1 Association Analysis in Financial Scenario-basic concept and idea 关联分析与金融应用——基本概念与思想
    • 9.2 Apriori Algorithm in Financial Scenario (1)-Introduction Apriori算法与金融应用——算法介绍
    • 9.3 Apriori Algorithm in Financial Scenario (2)-Candidate Generation & Pruning Apriori算法与金融应用——候选生成与剪枝
    • 9.4 Apriori Algorithm in Financial Scenario (3)-Hash Tree Apriori算法与金融应用——哈希树
    • 9.5 Apriori Algorithm in Financial Scenario (4)-Rule Generation and Complexity Apriori算法与金融应用——规则生成与算法复杂度
  • 10 Association Analysis with Financial Applications-FP Tree Algorithm 关联分析与金融应用——FP Tree算法
    • 10.1 FP Tree Algorithm in Financial Scenario-Introduction FP Tree算法与金融应用——算法介绍
    • 10.2 FP Tree Algorithm-A Financial Example FP Tree算法金融实例
  • 11 Financial Association Analysis Evaluation 关联分析在金融应用中的结果评估
    • 11.1 Financial Association Analysis-Evaluation (1) 关联分析在金融应用中的结果评估（1）
    • 11.2 Financial Association Analysis-Evaluation (2) 关联分析在金融应用中的结果评估（2）
  • 12 Cluster Analysis with Financial Applications-K-means Algorithm 聚类分析与金融应用——K-means算法
    • 12.1 Cluster Analysis in Financial Scenario-basic concept and idea 聚类分析与金融应用——基本概念与思想
    • 12.2 Introduction to K-means Algorithm in Financial Scenario K-means算法与金融应用——算法介绍与实例
  • 13 Cluster Analysis with Financial Applications-Basic Hierarchical Clustering Algorithm 聚类分析与金融应用——基本层次聚类算法
    • 13.1 Introduction to Basic Hierarchical Clustering Algorithm in Financial Scenario 基本层次聚类算法算法与金融应用——算法介绍
    • 13.2 A Financial Example of Agglomerative Hierarchical Clustering Algorithm 凝聚层次聚类算法实例
  • 14 Fiancial Cluster Analysis Evaluation 聚类分析在金融应用中的结果评估
    • 14.1 Unsupervised Cluster Evaluation 无监督的聚类结果评估
    • 14.2 Supervised Cluster Evaluation 有监督的聚类结果评估
Introduction to Naive Bayes Classifier in Financial Scenario 朴素贝叶斯分类器与金融应用——算法介绍


主要知识点：

  1. 贝叶斯公式

    如下图所示，其中P(Y|X)表示随机变量X取一个特定值时随机变量Y的条件概率，其和联合概率P(X,Y)相关，而联合概率又可以写成P(X|Y)P(Y)的形式，而分母是包含X的边缘概率。

  2. 贝叶斯定理是如何应用于分类问题

    给定属性值A={A1,...,An}的数据样本中观察到类别C的概率可以表示为P(C|A1A2...An)，这被称为目标类的后验概率，对应式（4）中左边的条件概率P(Y|X)。依据贝叶斯公式写出式（6），分子中P(A1A2...An|C)为类条件概率，测量属于C类别的样本中观察到属性值A的可能性。如果A确实属于C类别，那么期望该条件概率取值较大，对应式（4）的P(X|Y)。式（6）中，分子中P(C)是先验概率，用来捕获类别标签分布的先验知识，对应式（4）中的P(Y)。式（6）中分母为P（A1A2...An），这一项不依赖于类别标签，在后验概率的计算中可以被视为归一化常数，对应式（4）中的P(X)。因此，要想依据此式进行分类，关键的问题在于如何估计类条件概率P(A1A2...An|C)。

  3. 朴素贝叶斯分类器核心思想——对类条件概率的估计

    朴素贝叶斯分类器对类条件概率做了简化假设，其假设所有属性A的类条件概率可以被分解为类条件概率的乘积，即如下图所示，即给定类别标签C，属性值Ai是相互条件独立的，这意味着只有目标类别可以影响属性。

4.基于实际金融场景的朴素贝叶斯分类器类条件概率估算


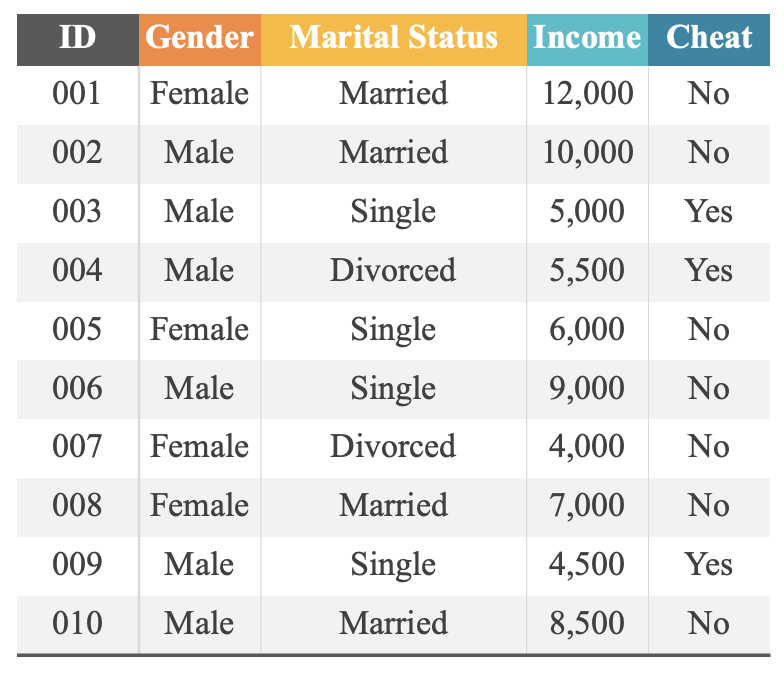
  • 计算条件概率P(Gender=Male|Cheat=No),通过前述内容可以得知其等于样本为No的训练样本中Gender=Male样本的比例，我们已经知道了训练数据集中共有7个数据对象的类别标签为no。在这7条数据对象中，共有ID=002,006,010三条数据对象的Gender属性值为Male，因此这个条件概率等于3/7。

  • 计算条件概率P(Income=12000|Cheat=No)，采用应用概率分布方法进行估算。假设条件概率服从高斯分布，通过训练数据集对该高斯分布的均值和方差进行估计。在类别标签Cheat=No的情况下，均值等于8071，而相应的方差为7035714，那么条件概率等于0.00005。