主要知识点：

1. 度量结点“纯度”（杂质度）的两个方法——基尼系数

决策树模型中，某个结点t的基尼系数如下图所示，其中是结点t中属于类别j的训练实例（数据对象）的相对频率。当结点里的实例在类别标签上呈现均等分布时，基尼系数取得最大值，代表“纯度”最低。相反，当结点里的实例只有一个类别标签时，基尼系数取得最小值，代表“纯度”最高。

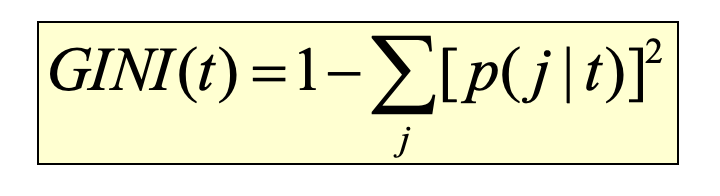
2.度量结点“纯度”（杂质度）的两个方法——熵

决策树模型中，某个结点t的熵的计算如下图所示，其中是结点t属于类别j的训练实例的相对频率。当结点里的实例在类别标签上呈现均等分布时，熵取得最大值，代表“纯度”最低，“杂质度”最高。相反，当结点里的实例只有一个类别标签时，熵取得最小值，代表“纯度”最高，“杂质度”最低。

为了更好的确定属性结点划分后的结果，我们可以计算划分前和划分后结点的“纯度”（杂质度）的差值。在经典的算法如ID3中，采用信息增益来对属性划分的结果进行度量，信息增益代表了信息复杂度（不确定性）减少的程度。对于一个特定的结点t而言，信息增益等于划分前（父结点）的熵减去划分后（子结点的集合）的熵。如下图所示：