1.1.1 粒径

颗粒粒径、几何学粒径(当量径)的概念。

(1)几何学粒径

①不规则颗粒的外接长方体和三轴径(l、b、h)

三轴径：在一水平面上，将一颗粒以最大稳定度放置于每边与其相切的长方体中，用该长方体的长度l、宽度b、高度h定义的粒度平均值。

②以外接长方体三维尺寸表示的不规则颗粒的粒径

几何平均径

算术平均径

(2)投影径：颗粒以最大稳定性置于一平面上，由此按其投影的大小定义的粒径

① Feret径，沿一定方向测得的颗粒投像两平行线间距离的平均值，又叫定方向径

② Martin径，沿一定方向等分颗粒投影像面积的线段长度的平均值(又叫定向等分径)

③ 割线径

④ 投影面积相当径：与颗粒投影面积相当的圆的直径

⑤ 投影周长相当径

(3) 筛分径：当颗粒通过粗筛网并停留在细筛网上时，粗细筛孔的算术或几何平均值。

算术平均值：(a₁+a₂)/2

几何平均值：(a₁a₂)1/2

(4) 球当量径－－能给出相同效果的球的直径

    ①等表面积当量径, D_S：是指与颗粒等表面积的球的直径

    ②等体积当量径, D_V：是指与颗粒等相同体积的球的直径

    ③等比表面积当量径, D_SV：是指与颗粒等比表面积的球的直径

    ④Stokes径(沉降), D_stk：指与颗粒具有相同密度且在同样介质中具有相同自由沉降速度（层流区）的直径

    ⑤光散射当量径：指用能给出相同的光散射密度的标准颗粒球直径表示的颗粒粒径

 1.1.2粉体的粒径分布

多颗粒体系存在粒径分布；粉体粒径分布的表示：频率分布和累积分布。

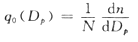频率分布，累计分布

1.1.2.2粒径分布函数

(1)正态分布（对称分布）

随机现象的概率模型－正态分布， 正态分布的概率密度函数(频率分布函数)：

                           

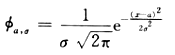
(2)对数正态分布（非对称）

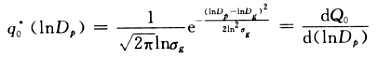
1.1.3平均粒径

① 设粉末是由粒径为d1, d2, …,dn的颗粒组成的集合体，其物理特性可表示为f(d)，可以由各个粒径函数的加成表示：

       
f(d)为定义函数，假设存在一个由直径为D的均一球形颗粒群，且该颗粒群具有与上述粒径不等的颗粒群相同的物理特性，即有f(D)=f(d)。则将D定义为平均粒径。

② 按照上述定义，可以以个数或质量为基准，针对某一物理特性推导出平均粒径。

如比表面积当量径

1.1.4颗粒的形状

1.1.4.1 颗粒形状的概念

① 颗粒形状是指颗粒的轮廓边界，是粒径之外颗粒的另一几何特征；

② 颗粒形状直接影响粉末体的性质，也直接与粉末在各种单元过程的行为相关；

③ 描述颗粒形状的方法：语言术语和数学术语。

1.1.4.2 形状指数和形状系数

1、形状指数：颗粒外形几何量的各种无因次组合。

(1)与外形尺寸相关的形状指数

       均齐度：以长方体为颗粒的基准几何形状

       长短度：长径/短径

       扁平度：短径/高度

(2)与表面积或体积相关的形状指数

       ① 体积充满度f_v：外接长方体体积/颗粒体积

       ② 面积充满度f_b：颗粒投影面积/最小外接矩形面积(lb)

③ 球形度f₀：颗粒接近球体的程度，与颗粒体积相等的球的表面积/颗粒的表面积。

     实用球形度f₀¢：与颗粒投影面积相等的圆的直径/颗粒投影的最小外接圆的直径。

(3)与颗粒投影周长相关的形状指数

      ① 圆形度f_c：表示颗粒投影与圆的接近程度，相同投影面积圆的周长/颗粒投影周长。

      ② 表面粗糙度x：颗粒投影周长/相同面积椭圆的周长。

2、形状系数

     研究物理现象和单元操作时要建立模型，模型建立基于规则颗粒，而实际颗粒不规则，应用模型时要引入修正系数

1.1.4.3颗粒形状的数学分析

(1)傅里叶级数展开的(R, q)法

(2)分数维法