完全信息静态博弈：混合策略均衡

混合策略均衡讲解提纲：

 1.混合策略均衡的提出

 2.混合策略均衡的计算

 3.完全信息静态博弈不同均衡概念之间的关系

1、混合策略均衡的提出——混合策略纳什均衡总会存在

表7 社会福利博弈
		流浪者
		寻找工作	游荡
政府	救济	3，2	-1，3
	不救济	-1，1	0，0

通过分析，我们可以发现在社会福利博弈中，不存在纯策略意义上的纳什均衡。

混合策略纳什均衡是这样一种均衡，在这种均衡下，给定其他参与人的策略选择概率，每个参与人都为自己确定了选择每一种策略的最优概率。

2、混合策略均衡的计算——参与人期望支付相等

表7 社会福利博弈
		流浪者
		寻找工作q1	游荡1-q1
政府	救济p1	3，2	-1，3
	不救济1-p1	-1，1	0，0

当政府选择“救济”时，其期望收益为3*q1+[-1*（1-q1）]

当政府选择“不救济”时，其期望收益为-1* q1+0*（1-q1）

3*q1+[-1*（1-q1）] =-1* q1+0*（1-q1）=>q1=1/5

表7 社会福利博弈
		流浪者
		寻找工作1/5	游荡4/5
政府	救济1/2	3，2	-1，3
	不救济1/2	-1，1	0，0

政府的混合策略为（1/2， 1/2 ）

流浪者的混合策略为（ 1/5， 4/5 ）

这一混合策略组合就是本博弈的混合策略纳什均衡

3、完全信息静态博弈不同均衡概念之间的关系

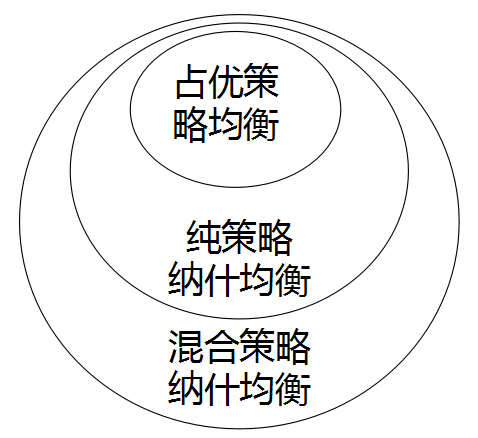
每一个占优策略均衡一定是纳什均衡，但并非每一个纳什均衡都是占优策略均衡。

即时纯策略的纳什均衡不存在，相应的混合策略纳什均衡却总会存在。