第一节 什么是正态分布
生活中大量随机变量的分布,呈现某种规律,变量两端分布少,变量中间部分分布多的形态
身高、体重、收入、婚龄、智商、高考成绩、官员廉洁……
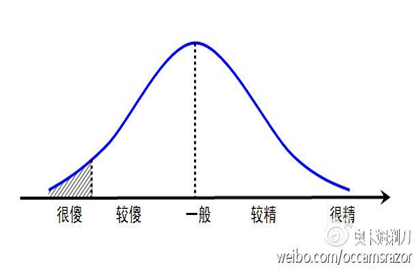
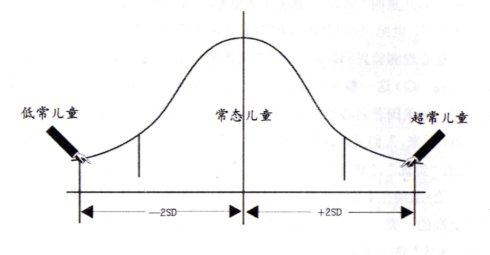
一、分布密度曲线j(x)
在相同变量范围内,概率大小与概率密度成正比;可以用概率密度分布表示概率的分布状况
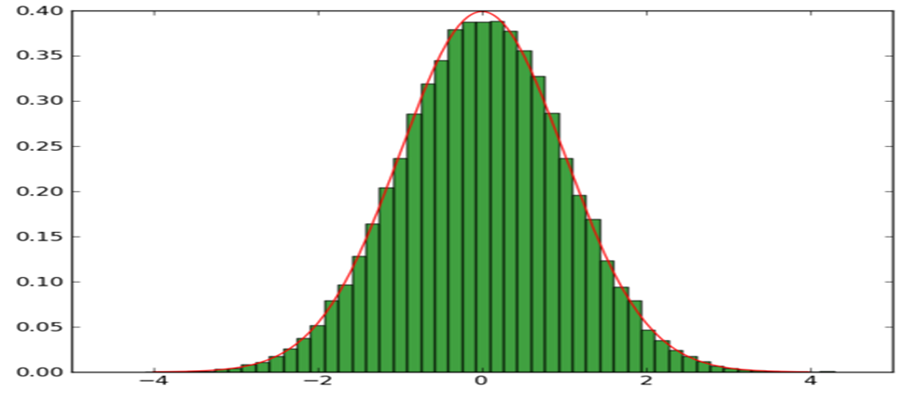
分布密度曲线具有对称起伏的形状,形成“钟型曲线”。它有三个特征:
(一)一个高峰:中间高,两边低
(二)一个对称轴:对称轴是直线x=m
(三)一个渐近线:以横轴为渐近线
正态分布的众值、中位值和均值三者必然是重叠的
正态分布——
它是一种概率分布,也称“常态分布”。正态分布具有两个参数μ和σ的连续型随机变量的分布。
服从正态分布的随机变量的概率规律为:取与μ邻近的值的概率大,而取离μ越远的值的概率越小;σ越小,分布越集中在μ附近,σ越大,分布越分散。
二、正态分布的概率密度表达式为
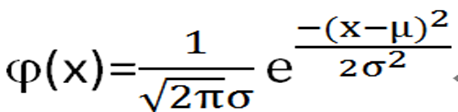
其中,p=3.14, e=2.72
m和s为正态分布曲线的两个参数,会对曲线形状产生影响
(一)j(x)在x=m处达到峰值,在x=m![]() s处有拐点,且以直线x= m为对称;
s处有拐点,且以直线x= m为对称;
当 一定的情况下,若m增大,图形右移;m减小,图形左移;图形形状不变;
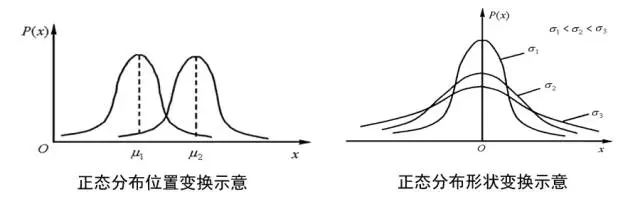
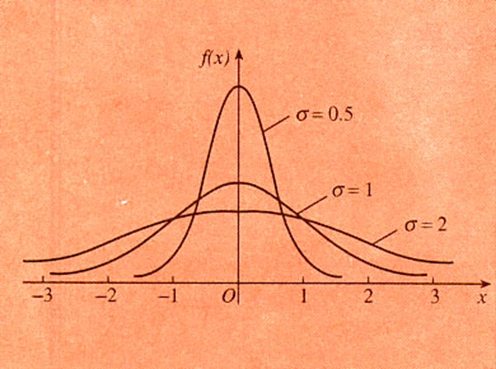
(二)当m不变,s越小,图形越尖瘦;s决定分布曲线的形状“高矮胖瘦”;(方差越小,密度越大;方差越大,密度越小)
m是正态分布曲线的数学期望或总体均值;s是正态分布曲线的标准差;
三、正态曲线下的面积
正态曲线下的面积,实际就是由无数个小直方形拼接而成的。每一小块面积代表的是随机变量e在该小块取值△Xi 所出现的概率。
每一块面积=长×宽=j(x) *△Xi =![]()
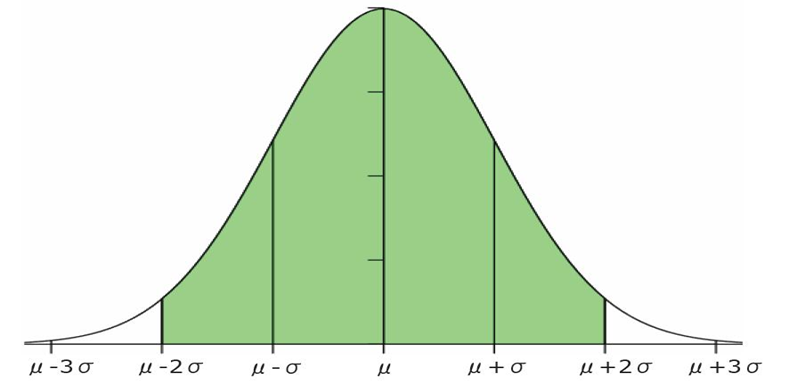
(一)变量取值在区间[m -s,m +s]之间的概率为0.6827
(二)变量取值在区间[m -2s,m +2s]之间的概率为0.9545
(三)变量取值在区间[m -3s,m +3s]之间的概率为0.9973


