在线教学视频：

课堂实录视频：

一、多圆锥投影

    1、概念

        在切圆锥投影中，离开标准纬线越远，变形越大。如果制图区域包含纬差较大时，则在边远地区产生相当大的变形，因此,采用双标准纬线圆锥投影比单标准纬线圆锥投影变形要小些。

        如果有更多的标准纬线则变形会更小些,多圆锥投影就是由这样的设想建立的。

        假设有许多圆锥与球面上的纬线相切，将球面上的经纬线投影在这些圆锥面上，然后沿同一母线方向将圆锥间开展平并在中央经线上拼接起来，就得到了所谓多圆锥投影。

        在多圆锥投影中，由于圆锥顶点不是一个，所以纬线投影为同轴圆弧。圆心在中央经线上，中央经线投影为直线。其他经线投影为对称中央经线的曲线。

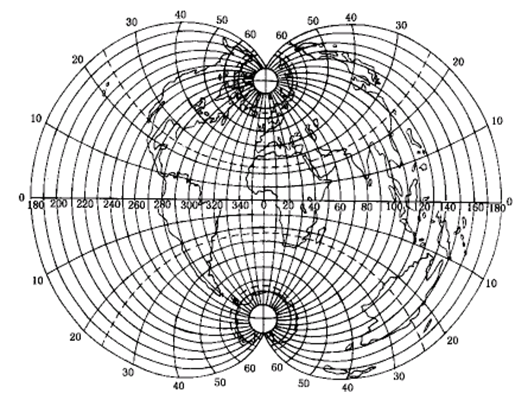
   由于多圆锥投影的经纬线是弯曲的曲线，具有良好的球形感，所以它经常用于编制世界地图。 

2、普通多圆锥投影

        普通多圆锥投影除了中央经线和每一条纬线的长度比等于1外，其余经线长度比均大于1，这个投影在中央经线上纬线间隔相等，在每一条纬线上经线间隔相等。普通多圆锥投影属于任意投影，中央经线是一条没有变形的线离开中央经线越远变形越大，这个投影适于做南北方向延伸地区的地图。美国海岸测量局曾用此投影做美国海岸附近地区的地图。

       普通多圆锥投影的另一个用途就是绘制地球仪用的图形。把整个地球按一定经差分为若干带，每带中央经线都投影为直线，各带的投影图在赤道相接，将这样的投影图贴在预制的球胎上，就是一个地球仪。 

感兴趣的同学请观看：地球仪制作

3、等差分纬线多圆锥投影

        我国地图出版社于1963年设计的一种不等分纬线的多圆锥投影。是我国编制“世界地图”常用的一种投影。

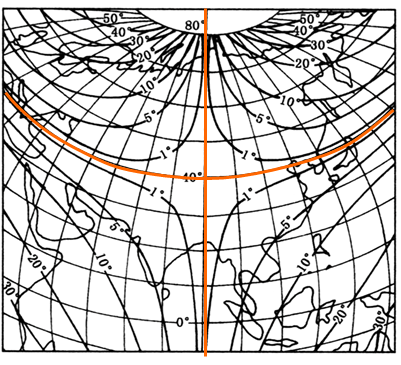
       这种投影的特点是：赤道和中央经线是互相垂直的直线，其他纬线是对称于赤道的同轴圆弧，其圆心均在中央经线上，其他经线为对称于中央经线的曲线，每一条纬线上各经线间的间隔，随离中央经线距离的增大而逐渐缩小按等差递减。极点为圆弧，其长度为赤道的1/2。 

        投影的变形性质属任意投影。 中央经线和纬线在44°交点处没有角度变形。我国境内绝大部分地区的角度变形最大在10°以内，少数地区在13°左右。

       我国绝大部分地区的面积变形在10%以内，面积比等于1的等变形线自东向西横贯我国中部。

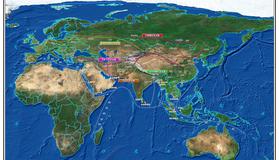
       我国位于地图的中央部位，图形较正确，图形上太平洋保持完整，利于显示我国与邻近国家的水陆联系。地图出版社用这一投影编制过数种比例尺的世界政区图和其他类型的世界地图。 

二、伪圆柱投影

        伪圆柱投影是在圆柱投影经纬线形状的基础上，规定其纬线投影的形状与圆柱投影相似即纬线为平行直线，经线则不同，除中央经线为直线外，其余的经线均为对称与中央经线的曲线。

       经线的形状是任意曲线。但通常选择为正弦曲线或椭圆曲线。

       按变形性质，伪圆柱投影没有等角投影,因为投影后经纬线不直交,所以只有等积和任意投影两种。

1、桑森投影（Sanson Projection）

        是一种经线为正弦曲线的等积伪圆柱投影。是法国人桑森于1650年所创。

        纬线为间隔相等的平行线，经线为对称与中央经线的正弦曲线，在每一条纬线上经线间隔相等。这种投影的所有纬线长度比均等于1。纬线长度无变形。中央经线长度比等于1，其他经线长度比均大于1，而且离中央经线越远，其数值越大。

        赤道和中央经线是两条没有变形的线离开这两条线变形越大。所以这两种投影适合于作赤道附近南北延伸的地区地图。 

2、摩尔魏特投影（Mollweide Projection）

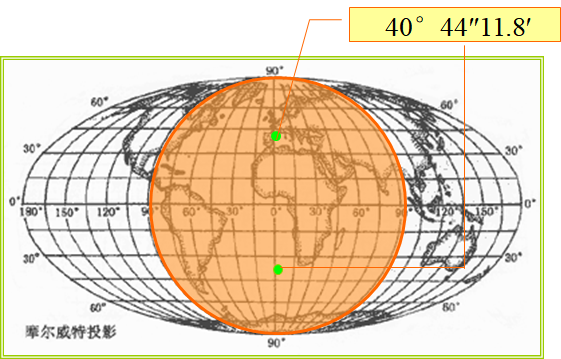
        是一种经线为椭圆曲线的等积伪圆柱投影。由德国人摩尔魏特于1805年设计而得名。    纬线为间隔不等的平行线，在中央经线上从赤道向南、北纬线间隔逐渐缩小；中央经线为直线，其他经线为对称与中央经线的同中心的椭圆，在离中央经线的经差正负90度的经线为一个圆，圆的面积等于地球面积的一半。在赤道上经线间隔相等。赤道长度比等于0.9，中央经线和南、北纬40°44″11.8′ 的两交点是没有变形的点，从这两点向外变形逐渐增大。

        这种投影常用在地图集和地理课本的封面上，英国1962年出版的飞利浦世界地图集中的世界地图采用这种投影 。

3、古德投影（Goode’s Projection）

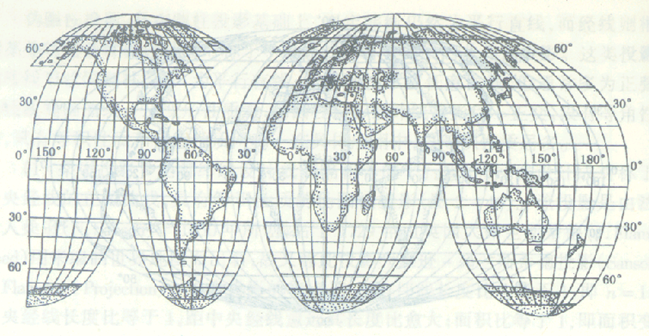
        从伪圆柱投影的变形情况来看离中央经线越远变形越大，为了减小远离中央经线部分的变形增大，美国地理学家古德于1923年提出了一种方瓣方法。就是在地图上几个主要制图区域的中央都定一条中央经线，将地图分为几个部分，按同一主比例尺及统一的经纬差展绘地图，然后沿赤道拼接起来，这样每条中央经线两侧投影范围不宽，变形就小一些。 

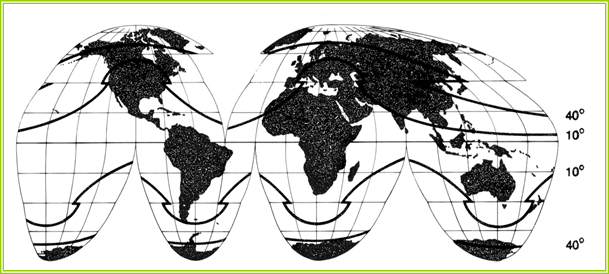
       这种分瓣方法可用于以上两种投影及其它伪圆投影。如适用于世界地图摩尔魏特——古德投影，为了摆正大陆的完态性，则在海洋部分断裂，古德分瓣方法如下：北美洲中央经线为西经100°；南美洲中央经线为西经60°；欧亚东经60°；非洲中央经线东经20°；澳大利亚中央经线为东经150°。如果为了完态的表示海洋则可在大陆部分断开。

        在国外出版的世界地图集中的世界地图经常采用这种投影，如美国出版的古德世界地图集中的世界各种自然地图，大多采用古德投影。 

三、伪圆锥投影

        伪圆锥投影是对圆锥投影的经纬线形状加以改变而成的。纬线形状类似圆锥投影为同心圆弧，圆心位于中央经线上，但经线则不同，除中央经线为直线外，其余的经线均为对称于中央经线的曲线。

        按投影的变形性质，伪圆锥投影没有等角投影，因为这种经纬线不直交，伪圆锥投影只有等积投影和任意投影，最常用的是等积伪圆锥投影。 

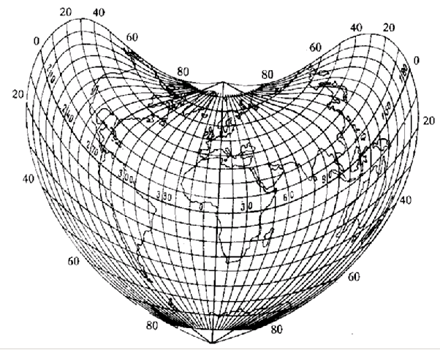
        等积伪圆锥投影，是由法国水利工程师彭纳于1752年首先提出，并用于法国地形图而得名。

        彭纳投影的纬线为同心圆弧，其长度比等于1；中央经线为直线，其长度比等于1，其他经线为对称于中央经线的曲线。在每一条纬线上的经线间隔相等，在中央经线上纬线间隔相等，中央经线与所有纬线正交。中央纬线与所有经线正交。

        彭纳投影没有面积变形，中央经线和中纬线是两条没有变形的线，离开这两条线越远变形越大。

        彭纳投影主要用于编制小比例尺的大洲图。 

                                

一些常见地图投影的经纬线形状特征 

投影名称	经线形状	纬线形状	中央经线上纬线间隔的变化	主要制图区域
正轴等角圆锥投影	放射状直线	同心圆弧	由地图中心向南北方向逐渐增大	中纬度地区分国图
正轴等积圆锥投影	放射状直线	同心圆弧	由地图中心向南北方向逐渐缩小	大洲图
正轴等距圆锥投影	放射状直线	同心圆弧	相等	中纬度地区分国图
墨卡托投影	间隔相等的平行直线	与经线垂直的平行直线	由低纬向高纬急剧增大	东南亚地区分国图
正轴圆柱投影   （任意）	间隔相等的平行直线	与经线垂直的平行直线	从赤道向两极逐渐增大	世界图
横轴等角圆柱投影	经线均为对称于中央经线并交于两极的曲线	纬线为对称于赤道并弯向两极的曲线	从赤道向两极逐渐增大	我国大中比例尺地形图
正轴等距方位投影	放射状直线	同心圆	相等	南北极地区图、南、北半球图
正轴等角方位投影	放射状直线	同心圆	从两极向赤道逐渐增大	南北极地区图、南、北半球图
等差分纬线多圆锥投影	中央经线为直线，其他经线为与中央经线对称的曲线	赤道为直线，其余纬线为对称于赤道的同轴圆弧	从赤道向两极稍有增大	世界图
彭纳投影	中央经线为直线，其他经线为与中央经线对称的曲线	同心圆弧	相等	亚洲图、欧洲图
摩尔威特投影	中央经线为直线，其他经线为椭圆弧	纬线是平行直线	由赤道向两极逐渐缩小	世界图、半球图
古德投影	中央经线是直线，其余经线是曲线	纬线是平行直线	纬度40°以下相等纬度40°以上逐渐缩小	世界图
桑逊投影	中央经线为直线，其他经线为与中央经线对称的曲线	纬线是平行直线	相等	非洲图、南美洲图