在线教学视频:
课堂实录视频:
一、圆柱投影的概念和种类
假定以圆柱面作为投影面,把地球球面上的经纬线网投影到圆柱面上,然后沿圆柱面的母线把圆柱切开展成平面,就得到圆柱投影。
当圆柱面和地球体相切时,称为切圆柱投影,和地球体相割时称为割圆柱投影。

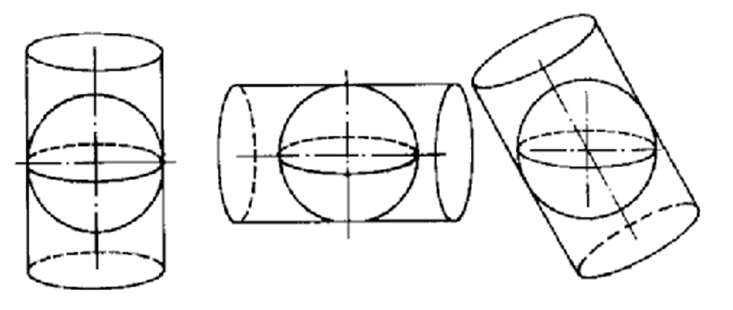
由于圆柱和球面相切相割的位置不同,圆柱投影又分为正轴、横轴和斜轴圆柱投影三种。
正轴圆柱投影——圆柱的轴和地球的地轴一致;
横轴圆柱投影——圆柱的轴和地轴垂直并通过地心;
斜轴圆柱投影——圆柱的轴通过地心,和地轴不垂直不重合。
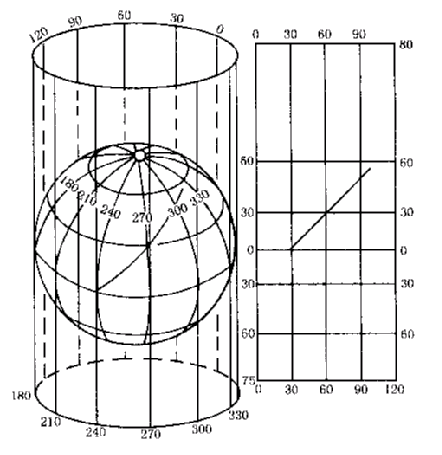
在上述三种投影方式中,最常用的是正轴圆柱投影,假定视点在球心,正轴圆柱投影中,经纬线网的特点是:
1.经线投影为平行直线,平行线间的距离和经差成正比。
2.纬线投影成为一组与经线正交的平行直线,平行线间的距离视投影条件而异。
3.和圆柱面相切的赤道弧长或相割的两条纬线的弧长为正长,无变形。
圆柱投影按变形性质可分为:等角圆柱投影、等积圆柱投影和任意圆柱投影。
二、等角正轴切圆柱投影(墨卡托投影)
等角正轴切圆柱投影是荷兰地图学家墨卡托于1569年所创,所以又称墨卡托投影。
在墨卡托投影中,赤道投影为正长,纬线投影成和赤道等长的平行线段,即离赤道越远,纬线投影的长度也越大。为了保持等角条件,必须把地图上的每一点的经线方向上的长度比和纬线方向上的长度比相等。所以在墨卡托投影中,从赤道向两极,纬线间隔越来越大。
在墨卡托投影中,面积变形最大。如在纬度60度地区,经线和纬线比都扩大了2倍,面积比P = m*n = 2*2 =4,扩大了4倍,愈接近两极,经纬线扩大的越多,在φ=80度时,经纬线都扩大了近6倍,面积比扩大了33倍,所以墨卡托投影在80度以上高纬地区通常就不绘出来了。
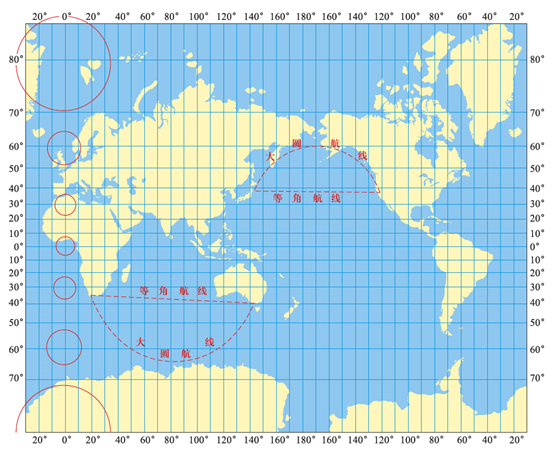
墨卡托投影被广泛应用于航海和航空方面,这是因为等角航线(或称斜航线),在此投影中表现为直线。
所谓等角航线,就是地球表面上与经线相交或相同角度的曲线,或者说地球上两点间的一条等方位线。
船只要按照等角航向航行,不用改变方位角就能从起点到达终点。
由于经线是收敛于两极的,所以地球表面上的等角航线是除经线和纬线以外,以极点为渐近点的旋转曲线。
墨卡托投影是等角投影,而且经线投影为平行直线,那么两点间的那条等方位螺旋线在投影中只能是连接该两点的一条直线。

等角航线在墨卡托投影图上表现为直线,这一点对于航海航空具有重要意义。
航行时,在墨卡托投影图上只要将出发地和目的地连一直线,用量角器测出直线与经线的夹角,船上的航海罗盘按照这个角度指示船只航行,就能达到目的地。
等角航线不是地球上两点间的最短距离,地球上两点间的最短距离,是通过两点的大圆弧(又称大圆航线或正航线)。大圆航线它各经线的夹角是不等的,因此它在墨卡托投影图上为曲线。
远航时,完全沿着等角航线航行,走的是一条较远路线,是不经济的,但船只不必时常改变方向。
大圆航线是一条最近的路线,但船只航行时要不断改变方向。如从非洲的好望角到澳大利亚的墨尔本,沿等角航线航行,航程是6020海里,沿大圆航线航行5450海里,二者相差570海里(约1000公里)。
实际上在远洋航行时:一般把大圆航线展绘到墨卡托投影的海图上,然后把大圆航线分成几段,每一段连成直线,就是等角航线。 船只航行时,总的情况来说,大致是沿大圆航线航行,因而走的是一条较近路线。但就每一段来说,走的又是等角航线,不用随时改变航向,从而领航十分方便。
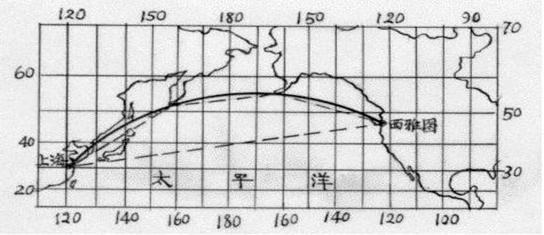
墨卡托投影图上的大圆航线与等角航线
三、等距正轴切圆柱投影
1、投影条件
圆柱面切于赤道,故赤道的投影为正长,经线投影后的长度不变。
2、特点及误差分析
赤道投影后无变形,纬线投影后,均变成与赤道等长的平行线段,离赤道越远,纬线投影后产生的误差也就越大。经线投影后为正长,为垂直于纬线的一组平行线,经线方向长度比为1,经线上纬线间隔相等。该投影的主方向就是经纬线方向。

用误差椭圆来分析投影误差规律和特点,误差椭圆的短半径和经线方向一致,且等于球面微圆的半径,长半径和纬线方向一致,且离开赤道越远伸长的就越多,误差越大。
面积变形、角度变形是离开赤道逐渐增大的。
当规定的经差和纬差相等时,经纬线网投影呈正方形网格,因此等距正轴切圆柱投影又简称圆柱投影或方格投影。
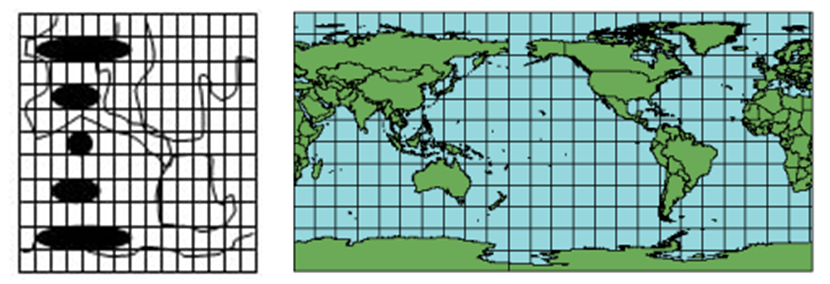
总 结
正轴圆柱投影特点:经纬线是互相垂直的直线,经纬线方向是主方向。切圆柱投影,赤道是一条没有变形的线,离开赤道越远变形越大,等变形线与纬线平行,呈平行线状分布。
根据圆柱投影变形分布规律,这种投影适合绘制赤道附近和沿赤道两侧呈东西方向延伸地区的地图。