在线教学视频：

一、地图投影的概念

在地球椭球面和平面之间建立点与点之间函数关系的数学方法，称为地图投影。

地图投影的实质是将地球椭球面上的经纬网按一定的数学法则转移到平面上。经纬线网是绘制地图的“基础”，是地图的主要数学要素。

建立 (x, y) 与 (φ, λ) 的关系

二、地图投影的变形

（一）投影变形的性质

（二）投影变形的研究方法

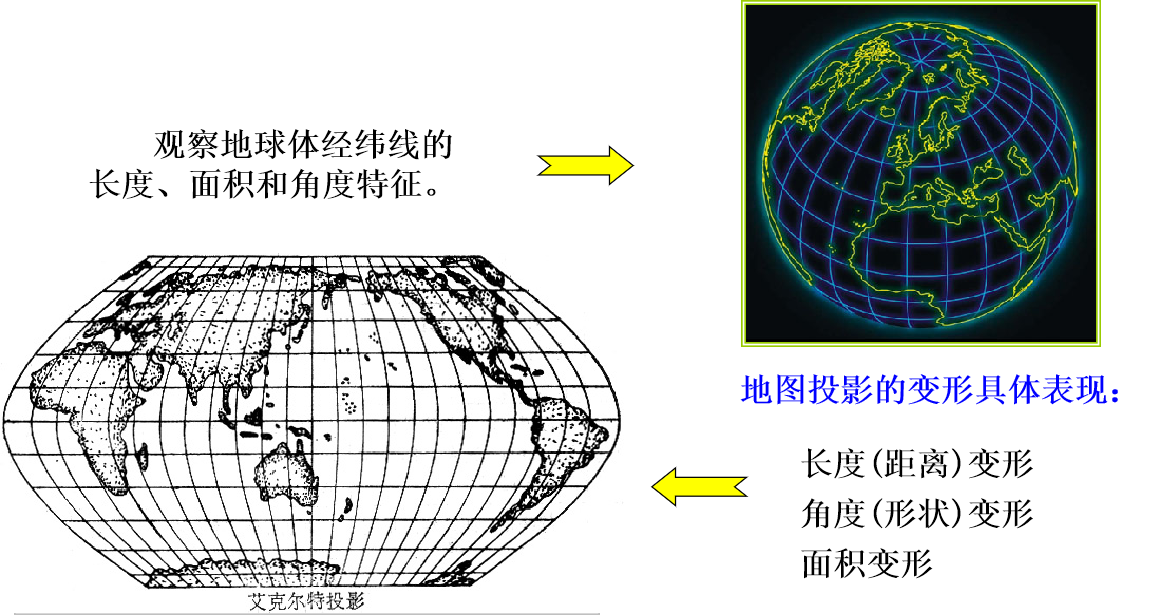
研究各种投影的变形规律是通过把投影后的经纬线网与地球仪上经纬线网格比较而实现的。

地球仪上经纬网的特点：

        所有经线圈都是通过两极的大圆；长度相等；

        所有纬线除赤道是大圆外，其余都是小圆，并且从赤道向两极越来越小，极地成为一点。

        经线表示南北方向；纬线表示东西方向。

        经线和纬线是相互垂直的。

        纬差相等的经线弧长相等；同一纬线上经差相等的纬线弧长相等，不同的纬线上，经差相等的纬线弧长不等，而是从赤道向两极缩小。

        同一纬度带，经差相同的经纬线网格面积相等，不同纬度带内，网格面积不等，同一经度带内，纬度越高，梯形面积越小。由低纬向高纬逐渐缩小。

（三）投影变形的相关概念

1.变形椭圆

在地球球面上取一微小圆，它在平面上的投影除在接触点位置外，一般情况下为椭圆。

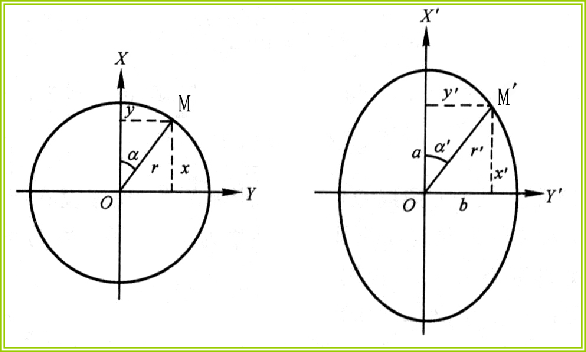
设o为球面上一点，以它为圆心的微小圆的半径是单位长度（为1），M(x, y)为圆上一点，圆心曲线方程为

x2+y2=1

o’为o的投影，以主方向作为坐标轴，M’（x’, y’）是M（x, y）的投影，令主方向长度比为a和b，则:

x’/x= a, y’/y= b

则:x =x’/a, y =y’/b

       (x, y)为圆上一点，将其代入圆的方程，得：

x’ 2/a2+ y’2/b2=1

这表明微小圆投影后为长半径为a短半径为b的椭圆，这种椭圆可以用来表示投影的变形，故叫做变形椭圆。

在研究投影时，可借助变形椭圆与微小圆比较，来说明变形的性质和数量。

    椭圆半径与小圆半径之比，可以说明长度变形。很明显的看出长度变形是随方向的变化而变化，在长短半径方向上有极大和极小长度比a和b，而长短半径方向之间，长度比μ，为b<μ<a。

    椭圆面积与小圆面积之比，可以说明面积变形。

    椭圆上任意两条方向线的夹角与小圆上相应的两方向线夹角之差为角度变形。     

2.长度比和长度变形

    设地球球面上有一微小线段ds，投影到平面上为ds’,如图所示。

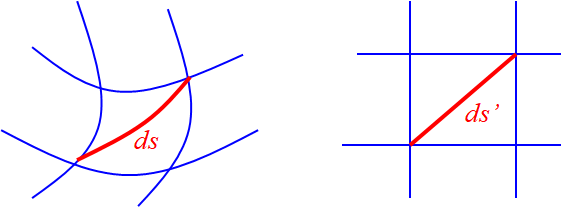
          平面上微小线段与球面上相应微小线段之比，叫做长度比。用公式表示为：

μ=ds’/ds

        长度比是一个变量，它不仅随着点的位置不同而变化，还随着方向的变化而变化。长度比是指某点某方向上微小线段之比。

通常研究长度比时，不一一研究各个方向的长度比，而只研究一些特定方向的长度比，即研究最大长度比（a）和最小长度比（b），经线长度比（m）和纬线长度比（n）。

        投影后经纬线成直交者，经纬线长度比就是最大和最小长度比。

        投影后经纬线不直交，其夹角为θ，则经纬线长度比 m、n和最大、最小长度比a、b之间具有如下关系：根据解析几何中阿波隆尼亚定理：

m2+n2 = a2+b2

m·n·sinθ = a·b

        用长度比可以说明长度变形。所谓长度变形就是长度比（μ）与1之差，用表v示长度变形则：v = μ-1

        由此可知，长度变形有正负之分，长度变形为正，表示投影后长度增加；为负，表示投影后长度缩短；为零，则长度无变形。

3.主方向

        由于投影要产生变形，所以球面上两条相互垂直的微小线段投影后不一定正交。如图设o是球面上两条互相垂直的微小线段，过o作两条垂线ac和 bd，投影后a’c’和b’d’。即地球面上角aob和角boc为直角投影后分别为锐角a’o’b’和钝角b’o’c’。

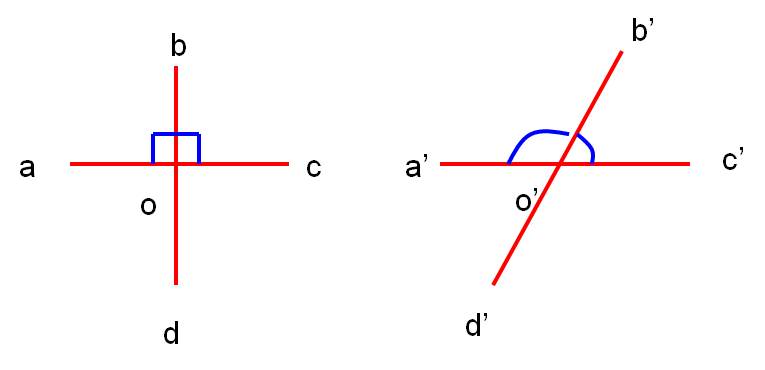
        设想ac、bd二垂线相对位置保持不变，并绕o点顺时针旋转，当旋转90度时，直角aob转到原来boc的位置，这时投影由原来的锐角转变成钝角；同样的，直角boc转到了cob的位置它的投影由原来的钝角变为锐角。由此可见，一个直角在不同的位置下的投影有着不同的大小，可以由锐角变为钝角，或者相反。那么在变化的过程中，必然有一特殊位置，直角投影后仍保持直交，此二直交直线方向，称之为主方向。

        在主方向上，具有极大和极小长度比。

        经纬线投影后为正交，经纬线方向均为主方向。但也有一些投影经纬网斜交，主方向与经纬线方向并不一致，这是主方向为经纬线以外的其他方向。

4.面积比与面积变形

      投影平面上的微小面积与球面上相应微小面积之比，称为面积比。以投影面上变形椭圆的面积dF’=abπ，相应球面上微小圆的面积dF = π12为例，以P表示面积比，则:

P = dF’/dF = πab/π12 = ab

       上式说明面积比等于主方向长度比的乘积。若经纬线方向是主方向时：

P = m·n

      若经纬线方向不是主方向时，则面积比:

       P=m·n·sinθ (θ为投影后经纬线夹角)

      面积比是个变量，它随点位置不同而变化。面积变形就是面积比与1之差，以Vp表示。

Vp = p-1

       面积变形有正有负，面积变形为零，表示投影后面积无变形；为正，表示投影后面积增加；为负，表示投影后面积缩小。

   5.角度变形

    投影面上任意两方向线所夹角与球面上相应两方向线夹角之差，称为角度变形。

   6.等变形线

        在各种投影图上，都存在着误差或变形。为了便于观察和了解绘制区域变形的分布。常用等变形线来表示制图区域的变形分布特征。等变形线就是变形值相等的各点的连线。

        等变形线在不同的投影图上，具有不同的形状。如在方位投影中，因投影中心点无变形，从投影中心向外变形逐渐增大，等变形线成同心圆状分布。

       等变形线通常是用点虚线来表示的。 

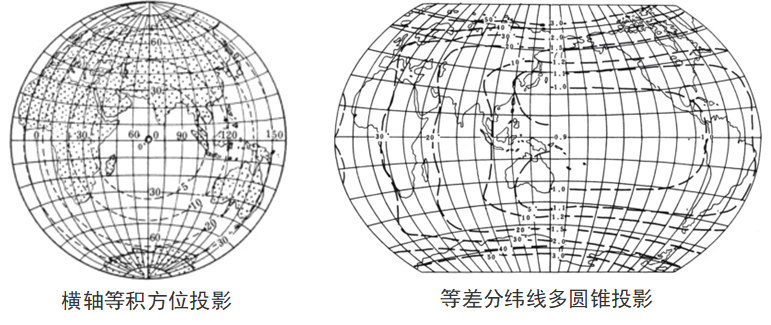
三、地图投影的分类

（一）按地图的投影方法分类

1. 几何投影  将地球经纬网透视投影到平面或几何面上。

（1）方位投影

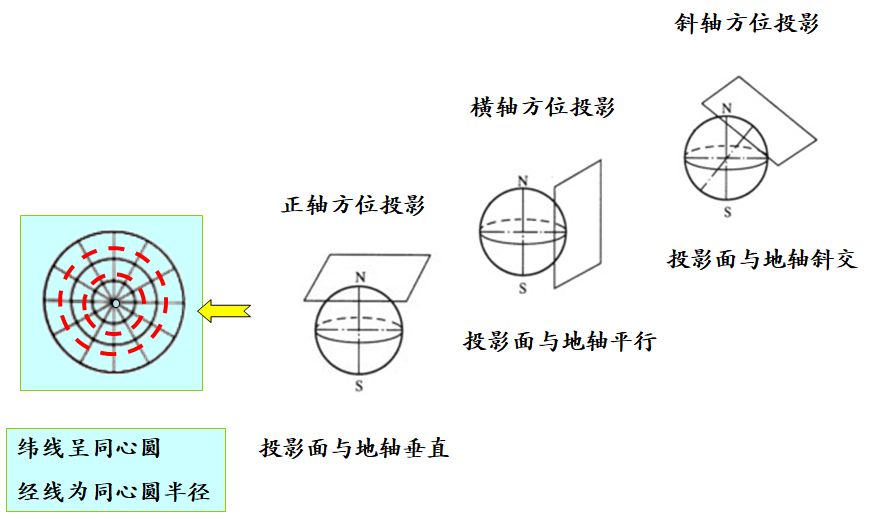
（2）圆柱投影

（3）圆锥投影

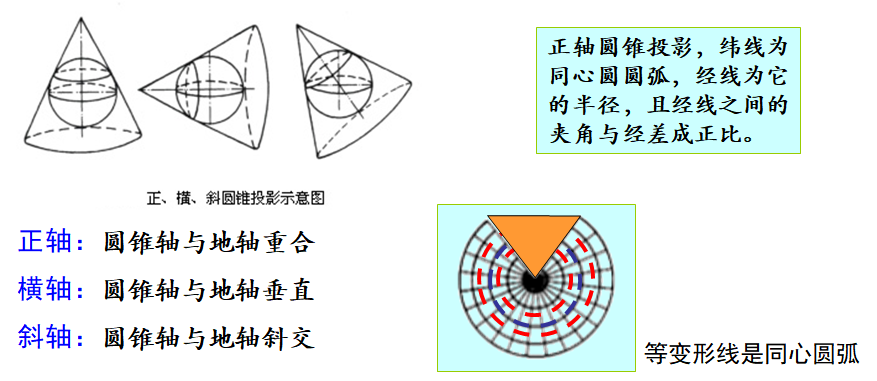
2. 非几何投影 不借助辅助投影面，通过数学解析方法得到。

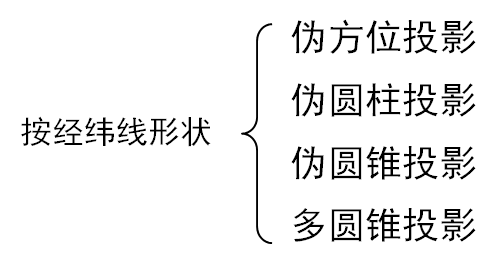
（1）正轴伪方位投影

纬线：投影为同心圆。

经线：除中央经线投影成直线外，其余经线均投影成对称于中央经线的曲线，且交于纬线的共同圆心。 

                              

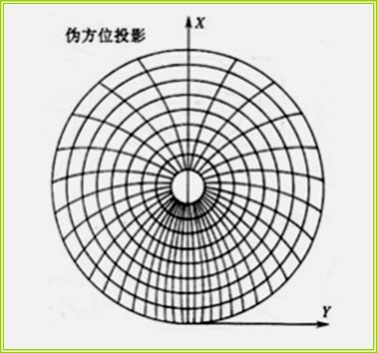
（2）伪圆柱投影

纬线：平行直线。

经线：中央经线投影成直线，其余经线均投影成对称于中央经线的曲线。 

（3）伪圆锥投影

在圆锥投影基础上，规定纬线仍为同心圆弧，除中央经线仍为直线外，其余经线则投影成对称于中央经线的曲线。

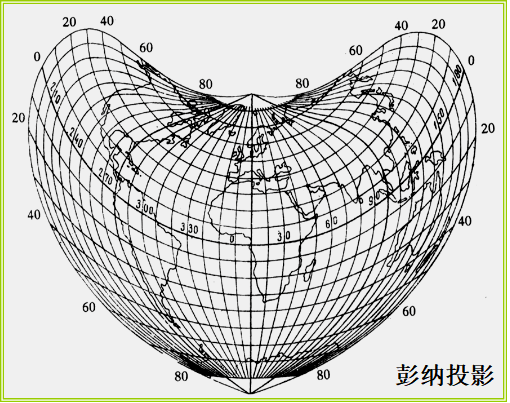
（4）多圆锥投影

        借助多个圆锥表面与球体相切设计而成的投影。

      纬线为同轴圆弧，其圆心位于中央经线上，中央经线为直线，其余经线则投影成对称于中央经线的曲线。 

（二）按地图投影的变形性质分类

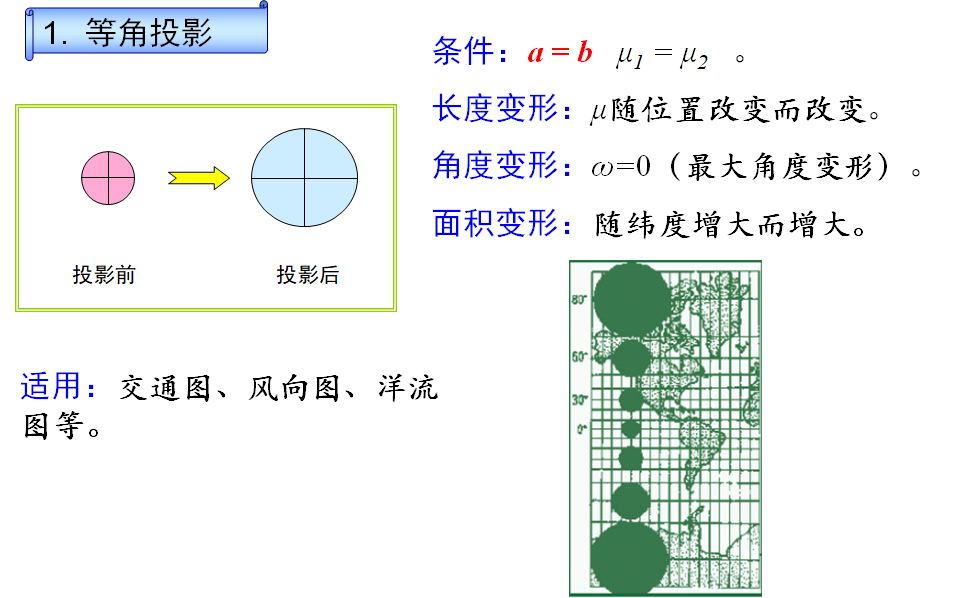
等角投影：投影面上某点的任意两方向线夹角与椭球面上相应两线段夹角相等。

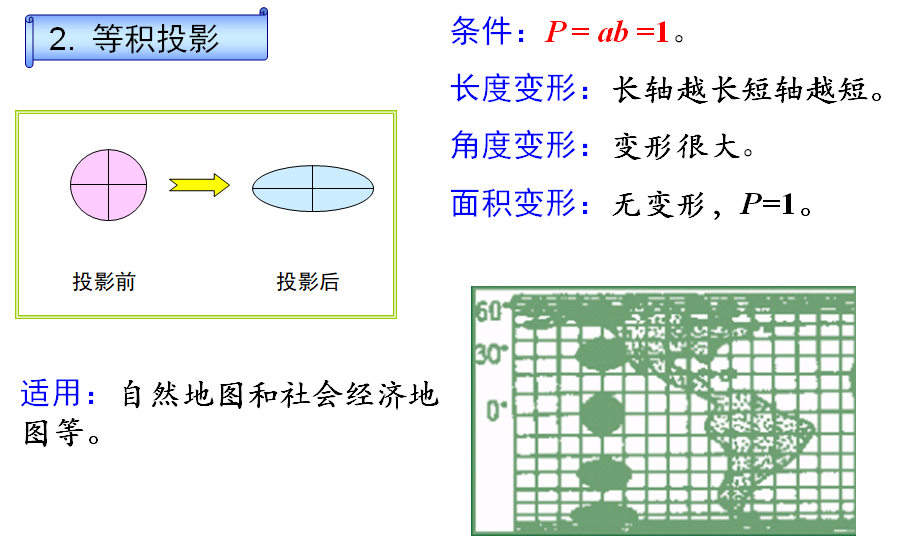
等积投影：投影面与椭球面上相应区域的面积相等。

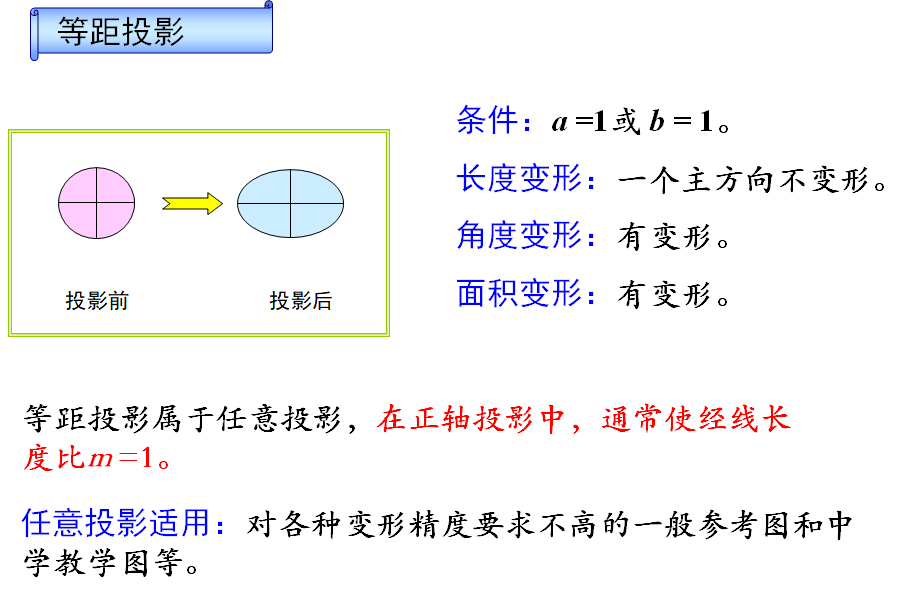
任意投影：投影图上，长度、面积和角度都有变形，既不等角又不等积。