20.5 逻辑代数

逻辑代数（又称布尔代数），它是分析设计逻辑电路的数学工具。虽然它和普通代数一样也用字母表示变量，但变量的取值只有“0”，“1”两种，分别称为逻“0”和逻辑“1”。这里“0”和“1”并不表示数量的大小，而是表示两种相互对立的逻辑状态。

一、常用的逻辑代数

1、常量与变量的关系

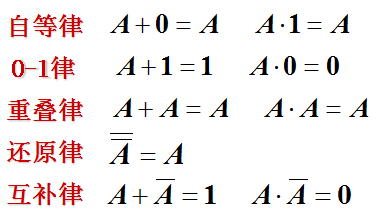逻辑与、逻辑或、逻辑非等

2、基本运算法则

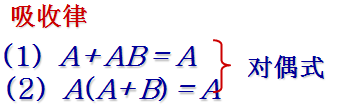
二、逻辑函数的表示方法

逻辑函数四种表示方法：真值表、逻辑表达式、卡诺图和逻辑图。

1、真值表

将n各输入变量的个状态及其对应的输出变量值列成一个表格。例如：某输入变n=3的逻辑函数的真值表如表所示：

2、逻辑表达式

通常是用与或式表示输入变量与输出变量逻辑关系的表达式。其中，或项的个数等于真值表中输出变量为1的个数，每个与项是对应的所有输入变量的原码（或反码）相乘（即最小项相乘）。上表的逻辑表达式可写成：

3、卡诺图

用方格组成的阵列图表示输入变量与输出变量的逻辑关系，阵列图中方格的个数等于输入变量所有状态的个数（个），每个方格用输入变量的状态编号，方格中填写输入变量状态对应的输出变量的状态。上表中逻辑函数可用下图的卡诺图表示。

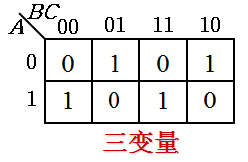
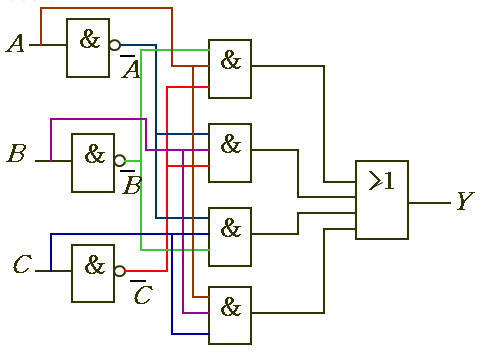
4、逻辑图

表示输入变量与输出变量逻辑关系的逻辑表达式，用相应的逻辑门电路符号连接起来的电路图。上述逻辑表达式的逻辑图如图所示：

三、逻辑函数的化简

1、化简要求

（1）化简为最简与或式（与项中的输入变量数最少，或项个数最少）；

（2）化简为与非式。

2、化简方法

（1）公式化简：用逻辑代数运算法则进行化简；

（2）卡诺图化简：按照卡诺图中方格为1的相邻原则，面积从大到小画圈进行化简，适用于输入变量n≤4的情况。

化简得到最简与或式的情况下，用还原律就可得到与非式。

具体的化简过程请参看PPT上的例题。