主要内容：

正弦量常用的相量表示方法以及相互转换。

重点难点：

正弦量常用的相量表示方法之间的相互转换，相量图和相量式的相互转

换。

内容精要：

  正弦量除了采用瞬时值表达式表示，或者用正弦波形图来表示外，还可

以用相量来表示。相量表示法的基础是复数，即用复数表示正弦量。

1.复数的表示形式及相互关系

设复平面有一复数 A，其模为 r，幅角为Y，如图1所示。它可以用以下几

种形式表示；

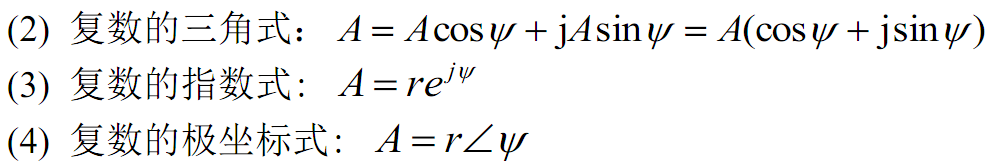
上述复数的四种表达形式，可以互相转换。

2．正弦量的相量表示

由上可知：复数由模和幅角两个特征来确定，而正弦量由幅值、角频率、

初相位三个特征来确定。在分析线性电路时，正弦激励和响应均为同频率

的正弦量，频率是已知的，可以不考虑。因此，一个正弦量由幅值(或有

效值)和初相位就可确定。比照复数，正弦量可用复数表示。

复数的模即为正弦量的幅值(或有效值)，复数的辐角即为正弦量的初相

位。

为了与一般复数相区别，把表示正弦量的复数称相量。用大写字母加“·”表

示。

若已知正弦电压为 u =U _msin(wt +y)，相量式可写为：

或 

注意，相量只是表示正弦量，而不是等于正弦量。