网络数据通常可以使用点线图（Node-LinkDiagram）和邻接矩阵（AdjacencyMatrix）来进行可视化（见图8-6）。两种方法有各自的优点和局限性，一般来说，点线图适合表示较小规模或较稀疏的网络，邻接矩阵适合表示较大规模或较稠密的网络。Ghoniem等人在（Ghoniemetal2005）中对这两种可视化的可读性进行了全面的评测。下面根据前文介绍的评测流程和框架对这项工作进行概略性介绍。

图8-6两种最常见的网络数据可视化形式：点线图（左图）和邻接矩阵（右图）。在点线图中，每个节点用圆表示，链接用连接相应节点的直线表示。在邻接矩阵中，节点沿横轴和纵轴排列。矩阵中每条链接所对应的位置用实心方块表示，不存在的链接对应的位置为空。

 

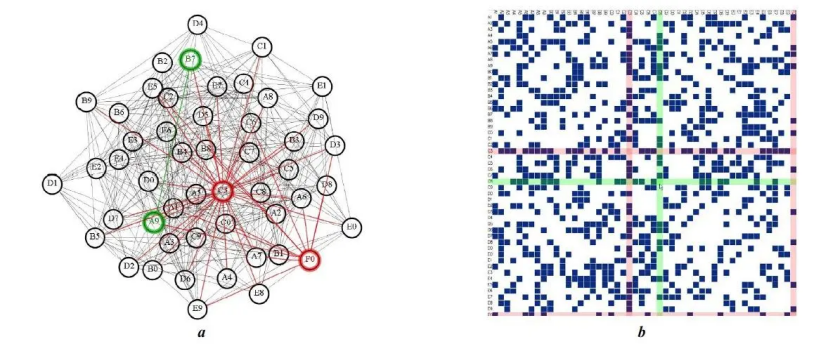
图8-6网络数据可视化的两种最常见形式

第一步：确定实验目标

首先决定在实验中用户需要完成的任务并选择相应的指标。在本项研究中，研究者关注的是两种可视化的可读性，且希望所做的分析有一定的通用性，可以不受数据的来源和领域限制。具体到网络数据，用户最关心的是与网络连接结构相关的信息。因此，可读性可以定义为用户从可视化技术了解一个数据中网络结构的难易程度。网络结构通常包括网络中节点、链接、路径和子网络。基于这样的数据特性，他们设计了下面的7个任务。

（1）估计网络中节点的数量。

（2）估计网络中链接的数量。

（3）找到网络中链接最多的节点。

（4）按照名字在可视化中找到对应的节点。

（5）找到两个节点之间的直接链接。

（6）找到两个节点之间的共同邻节点。

（7）找到两个节点之间的路径。

如果用户能够在短时间内正确地完成这些任务，就说明对应的可视化有较好的可读性。因此将用户完成这些任务的时间和正确率进行测量和统计作为评测可读性的基本指标。

第二步：准备实验

为了避免参与评测的用户接触过测试数据，研究者将使用随机生成的网络数据进行测试。基于对网络数据可视化的了解和经验，他们认为网络中节点的数量和链接的密度是影响可视化可读性最重要的因素。在之前的研究中，研究者发现，当链接的数量变多、网络的密度变大时，点线图可视化中由于链接之间的相互遮盖，网络的结构不清晰。因此，他们在实验中选取了三组不同的节点数量：20,50和100，以及三组不同的密度：0.2,0.4和0.6进行组合，总共随机生成了9个不同的网络。除此之外，研究者也根据所选取的任务，对生成网络数据的随机算法做了适当的调整。例如，第3个任务是找到链接最多的节点。随机生成的网络中可能出现有多个链接数量非常相近甚至一样的节点。为了让这个任务更清晰明确，他们决定给链接最多的节点再随机添加10%的链接。从这些细节可以看出，研究者在数据的选取时不但从评测的数据特性出发，也考虑了各个目标任务的需求。

在评测中，研究者招募了志愿参与者进行可用性评测。参与评测的用户共36人，包括硕士、博士研究生和从事计算机科学研究的人员。他们都对网络数据的点线图可视化有所了解。

两种可视化的实现和优化程度对于评测最终的结果是否有效也非常重要。对于点线图，研究者采用了可视化开源工具GraphViz（2012），使用的布局程序是neato。所有的图布局都提前生成，不占用用户完成任务和答题的时间。矩阵可视化由自己开发的可视化程序实现，其中节点在横轴和纵轴上按照名字的字母表顺序排列。两种可视化采用了相同的交互功能。当用户选中一个节点时，节点和它的链接被高亮标识；当选中一条链接时，链接和它的两端节点也被高亮标识。这些互动可帮助用户更快地完成任务。同时，为了保证用户完成任务时间的准确性，研究者对任务做了非常细致的安排。例如，第7个任务是找到两个节点之间的路径。这两个节点在可视化中被高亮标识，减少用户寻找指定的节点的时间，以记录用在寻找路径上的准确时间。

第三步：进行实验

在开始用户测试之前，研究者通过演示向测试者介绍如何正确地解读这两种可视化，并完成目标任务。其后，用户在研究者的帮助下尝试完成一些示范的任务，以确保他们对可视化方法、系统的交互和要完成的任务有准确的理解。

研究者严格地安排了任务和数据的前后顺序。每个用户从一种可视化开始，完成9个不同的网络图，每个图按顺序完成7个任务，然后换到另一种可视化完成同样的流程。两种可视化出现的前后顺序按照随机排列，保证了一半用户从点线图开始，而另一半用户从矩阵开始，最后的统计结果不存在因测试顺序而导致的偏差。在一个可视化流程中，9个网络图被分为两组，每一组中，图会按照随机顺序出现，以有效地避免学习效应。

在实验中，研究者对任务的时间进行了有效的安排和控制。用户一共需要完成126个任务（2个可视化×9个网络图×7个任务），每个任务限时45秒。如果时间结束，即使用户还没有完成任务，系统也会自动跳转到下一个任务。这种情况被解读为可视化无法帮助用户完成任务。由于任务比较多，因此在每组网络图之间和组中都提供了一定的休息时间。

第四步：分析结果

讨论实验所得到的结果主要包括完成任务的时间和正确率。研究者的目标不仅是总体的表现对比，还希望了解网络大小和密度对可视化可读性的影响。因此在分析结果时，详细比较了不同网络参数下的评测指标。图8-7和图8-8用柱状图分别表示了两种可视化技术、7个目标任务在不同网络图大小和密度下的平均完成正确率。图中浅色的条柱代表矩阵可视化的结果，深色的条柱代表点线图的结果。沿X轴分别是从第1～7个目标任务。不难看出，随着网络变大，密度增加，准确率也会下降。

研究者对网络图大小和密度这两个变量对回答时间的影响做了进一步的定量分析。他们采用线性回归得到线性模型中大小和密度的权重，由此更准确地了解到两种可视化方法的可读性对这两个参数的依赖性，以及在参数变化时的稳定性。

 

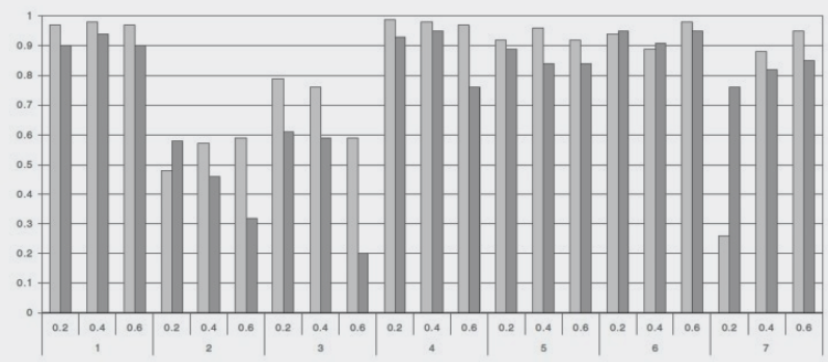
图8-7任务完成的正确率与网络大小

 

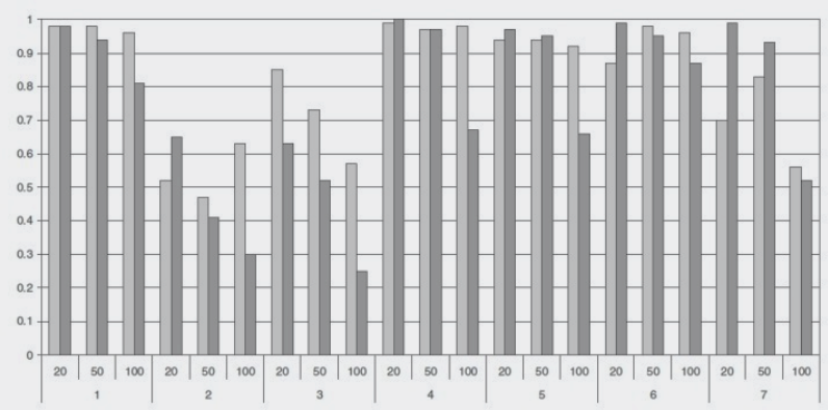
图8-8任务完成的正确率与网络密度。

其后发表的论文中，研究者对7个目标任务逐一进行了细致的分析。由于篇幅原因，我们在这里仅介绍任务1和任务7的分析结果。任务1是估计网络中节点的总数。图8.8中用盒须图表示了任务完成时间的分布。随着网络图变大，用户通过矩阵可视化完成任务的时间变化不大。而用户采用点线图的完成时间的中位值和方差都大大增加（见图8-9（a））。网络密度对两种可视化所对应的完成时间都影响不大（见图8-9（b））。总体而言，矩阵可视化对于任务1更为有效。图8.6和图8.7中对于任务1的正确率分析也显示了相似的特性。网络大小对点线图的表现有较大的影响。对于100个节点的网络来说，96%的用户通过矩阵可视化正确地得到了总的节点数，而使用点线图的用户只有81%的成功率。线性回归分析的结果：

TMX=18.8999−15.3938×d+0.157116×d×s

TNL=13.7151−10.6864×d+0.302776×d×s

 

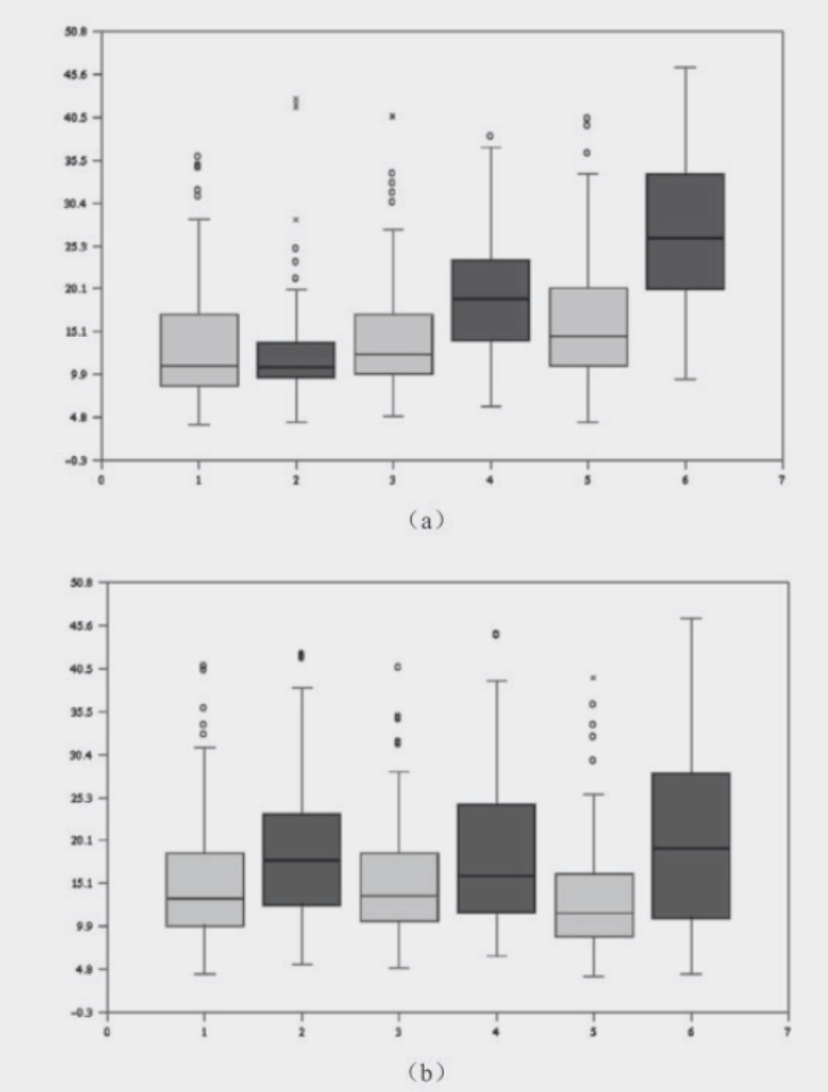
图8-9任务1（估计节点数量）所花时间的盒须图。

研究者分析上述的线性模型，认为与图8.8基本一致，点线图的可读性受到网络大小和密度综合作用的影响较大。

浅色的代表矩阵可视化，深色的代表点线图。（a）沿X轴，每一组分别代表不同大小的网络。（b）沿X轴，每一组分别表示不同密度的网络。

任务7是找到两个节点之间的路径，即找到一系列连接两个节点的链接。图8-10中的结果显示，对于点线图，网络图越大，所需要的时间越多，网络密度对完成时间影响不大。矩阵表示则不同，网络密度越大，所需要的完成时间越短。对于节点较少且密度小的网络，矩阵可视化在寻找路径上并不如点线图有效。但是，对于高密度的大网络，矩阵可视化反而更有效。研究者对此的推测是，当网络密度增大时，任意两个节点更有可能直接相连，因此寻找路径简化为寻找两点之间直接链接的任务，矩阵可视化变得更为有效。图8-7和图8-8中的任务完成正确率表现了完成时间相似的规律。线性回归分析的结果：

TMX=45.7229−53.507×d

TNL=6.05372−23.2979×d+0.445508×s−0.397442×d×s

 

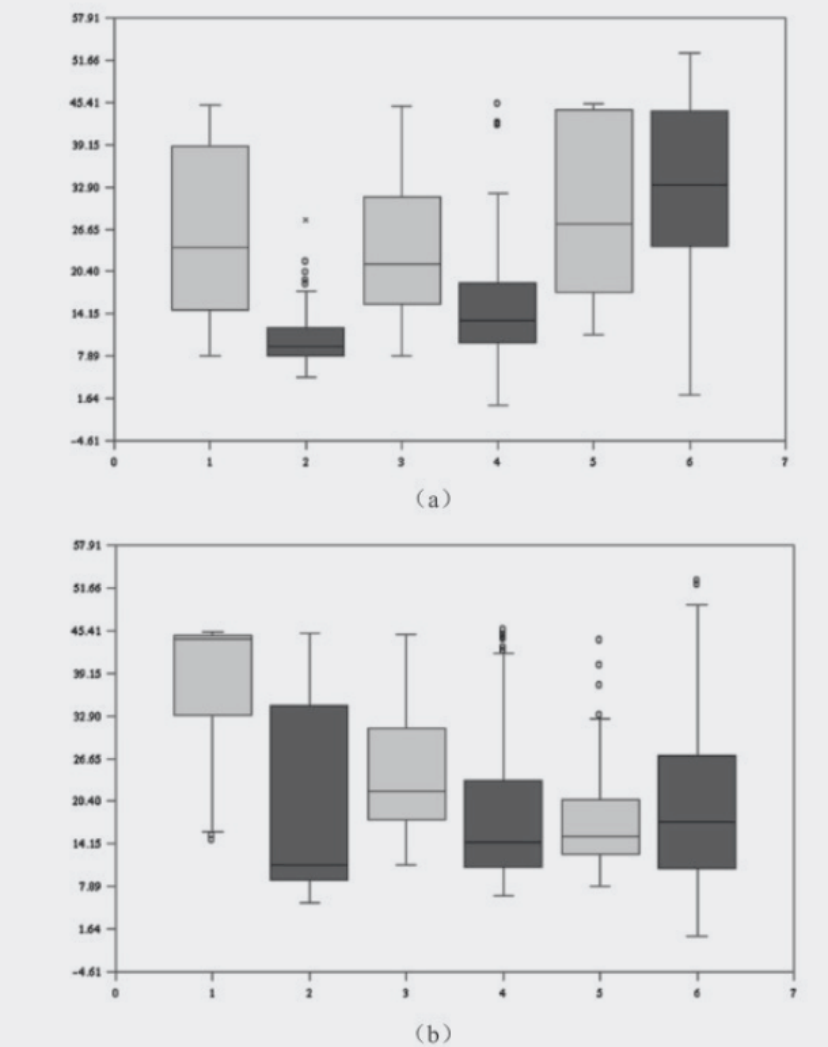
图8-10任务7（找到两个节点之间的路径）所花时间的盒须图

研究者分析上述的线性模型，认为与图8.8基本一致，点线图的可读性受网络密度的影响较大，而矩阵的可读性则随着网络密度增加而改善。

最后，研究者从可读性评测得出的结论是：点线图的可视化适用于较小的网络数据，而邻接矩阵可视化则更适合于密度较大的大网络。另一方面，除搜寻路径的任务之外，邻接矩阵可视化的可读性高于点线图。当前邻接矩阵在网络数据可视化中的使用较少，研究者建议人们更多地关注矩阵可视化并使用到实际应用中。