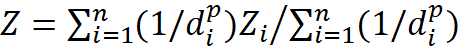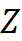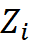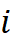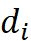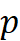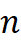4.4 空间插值
4.4.1 空间插值概述
4.4.1.1空间插值
在地理观测过程中，基于成本和必要性的考虑，人们只需要对区域进行采样，观察和获取区域内特征位置上的数据，只有在采样点上的数据才是实际获取的，未采样的点上是没有数据的。为了获得未采样点上的数据，需要将已获取的样本点数据按照一定的法则扩展开来，给未采样点赋予一个合理的值，这就是空间插值。
空间插值就是利用已知样本点的数据来估算其他点的数值的过程。在GIS中，空间插值需要根据已知点的值来估算栅格中每个像元的值。通过空间插值，可以将点数据转换成面数据，形成一个栅格表面以用于空间分析或建模。
空间插值的理论源于地理学上的一个基本定律——相近相似或相近相关，也有人称之为地理学第一定律。即在空间位置上越接近的点，具有越相似的特征，反之相似性越低。
进行空间插值有两个必不可少的条件：控制点和插值方法。
4.4.1.2控制点
控制点是用于空间插值中的已知数值的点，也叫观测点、样本点。控制点的获取是进行空间插值的必要前提。控制点的数目和分布对空间插值精度的影响是巨大的。为了获得更好的插值效果，控制点的选取应尽量合理。一般来说，控制点需要尽可能多，而且分布均匀，最重要的是它们能够反映要素空间分布的主要轮廓特征。
4.4.1.3空间插值的方法及分类
1．空间插值的常用方法
空间插值的方法有很多，包括反距离权重法、样条函数法、克里金插值法、自然邻域法、趋势面法、径向基函数法等插值方法。
2．空间插值的方法分类
（1）确定性插值和随机性插值。确定性插值方法以研究区域内部的相似性或平滑度为基础，根据已知样本点的值，采用特定的数学函数进行插值生成预测表面。随机性插值方法利用样本点的统计属性，对样本点之间的空间自相关进行量化，并考虑到预测位置周围的采样点的空间配置，用估计变异提供预测误差的评价。
（2）全局拟合插值和局部拟合插值。全局拟合插值以整个研究区的样本点数据为基础，通过构建一个数学函数来对表面进行拟合从而估算未知点的值，常用于估算表面的总体趋势。局部拟合插值则是利用邻近的部分已知样点的数据来估算未知点的值，用来估算局部或短程的变化。
（3）精确性插值和非精确性插值。精确性插值所生成的表面通过所有的已知点，而非精确性插值的表面则不一定通过。非精确性插值可以有效避免输出表面中出现明显的凸起或凹陷。
3．ArcGIS中的空间插值工具
ArcGIS中用于空间插值的工具主要有两个部分，一是空间分析工具集中的各类插值工具（Interpolation）。二是地统计分析扩展模块，它在ArcToolbox中有地统计分析工具集，并在ArcMap中有地统计分析工具条用于空间插值。
4.4.2 反距离权重法
反距离权重法（InverseDistance Weighted，IDW），又称为距离反比加权法，它以待插值点与若干邻近样本之间的距离倒数为权重，采用加权平均的方式来计算待插值点的值，属于确定性的内插方法，也是一种局部拟合方法。反距离权重法基于相近相关的原理，认为距离越近的点对待插值点具有较大的影响，而距离越远的点对待插值点的影响较小（即作用的大小与距离的大小呈反比）。该方法假设各已知采样点对待插值点的预测值都有局部影响，其影响随着距离的增加而减小，离待插值点近的已知采样点在预测过程中所占的权重大于离待插值点远的已知采样点的权重。其一般公式为：
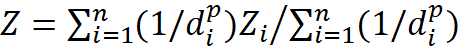4.32
式中：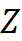
是某待插点的值，
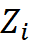是第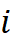
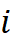（=1，2，…，n）个已知采样点的值，
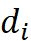是第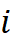个已知采样点与待插点的距离，
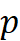是幂指数。
反距离权重法计算出的表面受幂值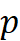和邻域搜索策略的影响很大。
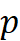值用于控制权重值的降低速度，其大小对插值结果有显著的影响。随着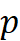值的增大，较远样本点的权重将迅速减小，近处样本点的权重比例迅速增加，拟合的表面不够光滑，有更多的细节。
确定用于插值的邻近样本点有两种处理模式：一是指定近邻点的数量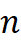
，将最近的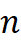个点用于插值。同时通过设定最大搜索距离，限制最邻近采样点个数。二是设置搜索的邻域范围来确定样本点，同时设置最小邻近采样点数量。
反距离权重法是一种精确性插值方法，生成的表面通过所有样本点，且表面内的最大值和最小值只能出现在采样点处。反距离权重法便于理解，易于计算，在样本点分布较为密集且分布较为均匀，可以得到较好的插值效果。该方法主要的不足在于没有充分考虑样本点的空间分布，在样本点分布较为稀疏的地点插值结果会产生较大的偏差，并且当待插值点附近的样本点数据很大或很小时，待插值点的结果容易受极值的影响而产生明显的“牛眼”现象。
4.4.3 自然邻域法
自然邻域法插值（NaturalNeighborhood）与IDW法类似，都是采用与待插值点相邻的样本点进行加权平均而估算。
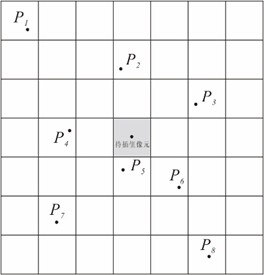
自然邻域法插值的基本过程如下（图4.78）：（1）用所有已知样本点（图中的小黑点）构建泰森多边形（图中的黑色粗线）；（2）用待插值点（五角星）与周边的已知样本点重新构建一个新的泰森多边形（图中的虚线）；（3）将与新泰森多边形相邻的点用于插值（图中编号的6个点）；（4）计算新泰森多边形在每个原泰森多边形中的面积比例（重叠比例），作为相邻样本点的权重；（5）计算相邻点的加权平均值。
可以看出，自然邻域法插值与IDW不同的是，用于插值的相邻样本点的选择方法及权重的计算方法不同。
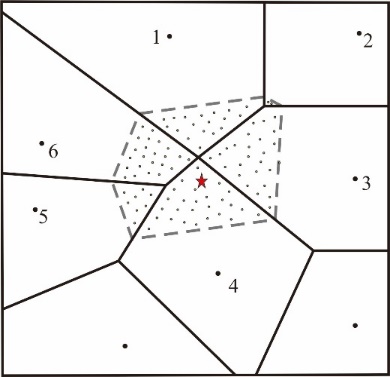
图4.78 自然邻域插值中点与权重的确定
4.4.4 样条函数值法
样条函数法（splines）是利用最小化表面总曲率的数学函数来估值，生成恰好经过样点的平滑表面，同时保证了由样点连接形成的所有表面斜度变化最小。基本思想就是采用分段多项式逼近已知数据点同时又保证在各段交接的地方有一定的光滑性。形象的说，样条函数插值就类似在拉伸一片橡皮膜，使之通过所有的样本点并保证曲率最小。样条函数插值适合于模拟高程、气温、降水、污染物浓度等空间连续变化并且较为光滑的表面。
样条函数是分段函数，进行一次拟合只用少数邻近点，同时保证曲线段在连接处为平滑连续曲线。
样条函数插值的结果主要受插值类型和权重的影响。插值的类型主要有两种：规则样条函数（Regularized）和张力样条函数（Tension）。规则样条函数生成一个平滑、渐变的表面，且插值的结果可能会超过采样点数据范围，其权重值控制着表面的平滑度，权重越大表面越平滑；张力样条函数可以根据建模现象的特征来生成一个相对不太平滑的表面，但内插值更接近采样点数据的值域范围之内，其权重值控制着表面的弹性值，权重越大，表面越粗糙。
与IDW相比，样条函数也属于精确性插值，生成的表面通过所有已知样本点，但该表面更为平滑，其内插值并不局限于控制点的最大值与最小值范围内，一般不适用于短距离内属性有较大变化的地区，在样点稀疏的地方拟合结果会出现较大的偏离问题。
4.4.5 趋势面法
趋势面法（Trend）插值是一种全局多项式插值（Global polynomial interpolation，GPI）方法，它根据样本点的属性值和空间坐标的关系，对整个区域的样本点采用全局多项式、基于最小二乘法进行拟合，生成一个反映要素整体渐变趋势的平滑表面。在概念上，趋势法插值类似于取一张纸，将其插入各凸起点之间，实际情况下，平整的纸张是无法完全模拟包含山谷的地表，于是将纸张略微弯曲，模拟效果将会更好。平面是一个一阶多项式（线性），二阶多项式允许1次弯曲，三阶多项式允许2次弯曲，以此类推。
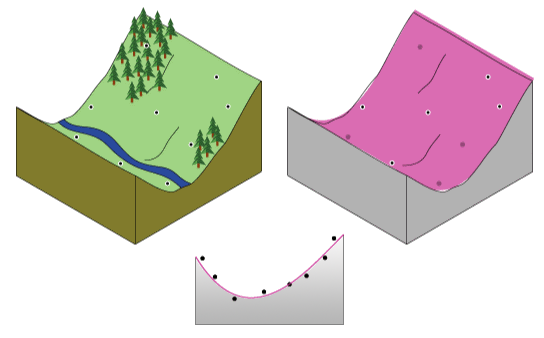
图4.80趋势面插值示意图
趋势面法将样本点的实测值分解为三个部分：全局趋势、局部变异、随机干扰。
根据最小二乘法原理，计算多项式系数，得到趋势面方程，利用该方程可计算趋势面中任意一点的估算值。为求取多项式系数，一次、二次、三次多项式分别需要至少3个、5个、9个点的样本点数据。
拟合表面多项式的次数越低，拟合的表面越粗糙，拟合效果越差，仅能反映区域的宏观趋势。次数越高，拟合面越光滑，拟合结果更接近于实际表面。但是，插值中并非次数越高越好，次数过高使得计算量大大增加而精度提高不大，一般选择二次或三次即可。
趋势面法适用于对整个区域而不是对具体的某一个地区进行插值，虽然拟合结果不一定在局部很符合输入的样本点，但是在总体上是非常符合的。此外，它还可用于检查或排除长期或全局趋势的影响。趋势面法插值容易受极值点的影响，尤其是在研究区的边沿地带。此外，它对样本点的要求很高，若样本点不能真实反映要素变化的重要因素（如周期性和趋势），则内插不能取得很好的效果。
4.4.6 局部多项式法
局部多项式插值（Local polynomialinterpolation，LPI）将一个复杂的表面分解为很多部分，每个部分利用该局域范围内的已知样本点，采用一个多项式来进行拟合，这样整个表面将由多个多项式拟合而成。每个多项式只在特定重叠的邻近区域内有效，可以通过设定搜索半径和方向来定义一个以待插值点为中心的邻域，还可以通过设定参与待插值点估算的样本点数最大值和最小值来定义邻域。由此可见，局部多项式插值能够很好拟合表面中的短程变异，体现表面中的局部特征，从而产生一个更为准确、真实的表面。
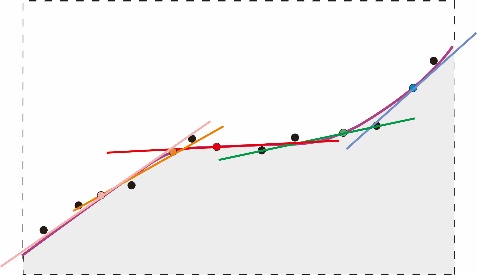
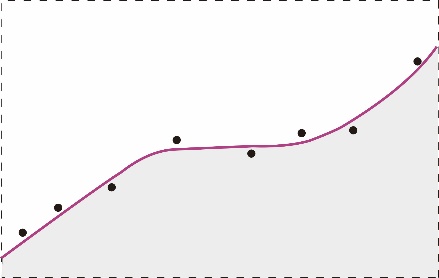
图4.81局部多项式表面拟合
局部多项式插值法的实质是一种局部加权最小二乘方法，它有以下四个基本步骤：
（1）选择插值函数。
（2）确定搜索的相邻样本点。
（3）参数设置。
（4）计算待插值点的值。
4.4.7 径向基函数法
径向基函数（Radialbasis functions，RBF）又称为径向基神经网络，是人工神经网络方法中的一种。它包括以下五种不同的基本函数：平面样条函数(Thinplate spline)、张力样条函数(Spline with tension)、完全规则样条函数(Completelyregularized spline)、高次曲面函数(Multiquadricspline)、反高次曲面函数(Inversemultiquadric spline)。采用不同的基本函数决定了插值时将以不同的方式使表面通过所有的已知样本点，从而也得到不同的插值表面。径向基函数插值得到的表面不仅能够反映整体趋势，而且还能反映局部变化。
径向基函数法是一种精确性的插值方法，拟合的表面必须通过每一个已知的样点，在这一点上，它与趋势面法（全局多项式法）和局部多项式法的非精确性插值都有所不同。
RBF可以说是样条函数的一个特例，适用于对大量点数据进行插值计算从而获得平滑表面，在将其应用于变化平缓的表面（如高程、污染物浓度等）时能得到令人满意的插值效果。但在表面值的变化较为剧烈、无法确定采样点数据的准确性、采样点的数据具有很大的不确定性等情况下，不适宜采用本方法。
与IDW相比，RBF更加灵活，有更多的参数设置，可以预测比采样点高或低的未知点的值，而IDW无法计算高于或低于采样点的预测点的值。
4.4.8 插值结果的验证
插值结果是否能很好模拟要素表面，需要进行验证。验证的方法主要有两种，即交叉验证（Cross Validation）和实际验证。交叉验证法首先假定每一样本点的要素值是未知的，采用周围样本点的值来估算（即待评估的样本点不参与插值），然后计算所有样本点实际观测值与内插值的误差，以此来评判估值方法的优劣。实际验证法将已知的样本点分为两部分，一部分作为“训练数据集”（如随机选择85%的数据）用于空间插值；另一部分作为“验证数据集”不参与插值计算。将基于训练数据集的插值结果与验证数据集中的值进行对比，从而确定插值效果。
验证插值结果的具体指标包括：（1）标准平均值预测误差（Mean Standardized，MSE）接近于0；（2）均方根预测误差(Root-Mean-Square，RMSE)较小；（3）平均标准误差(Average Standard Error，ASE)与均方根预测误差接近；（4）标准均方根预测误差(Root-Mean-Square Standardized)接近于1；（5）平均误差（Mean Error，ME）、平均相对误差（Mean Relative Error，MRE）和平均绝对误差（Mean Absolute Error，MAE）较小；（6）标准均方根误差（Normalized Root Mean Square Error，NRMSE）越小，插值的精度越高，误差越小。
4.4.9 插值实例
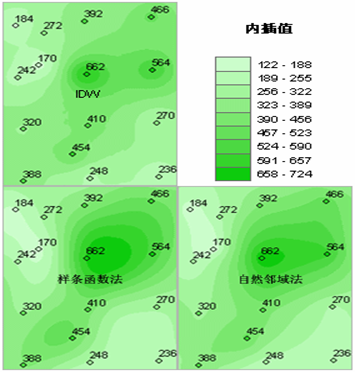
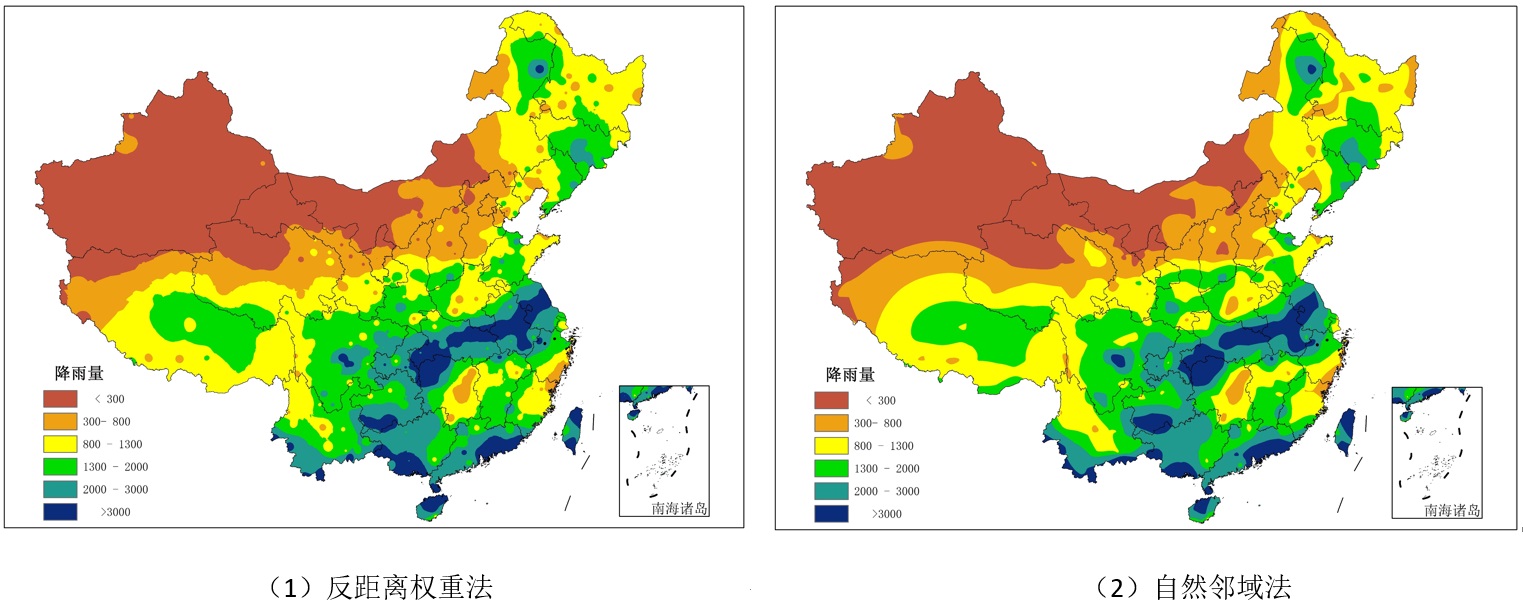
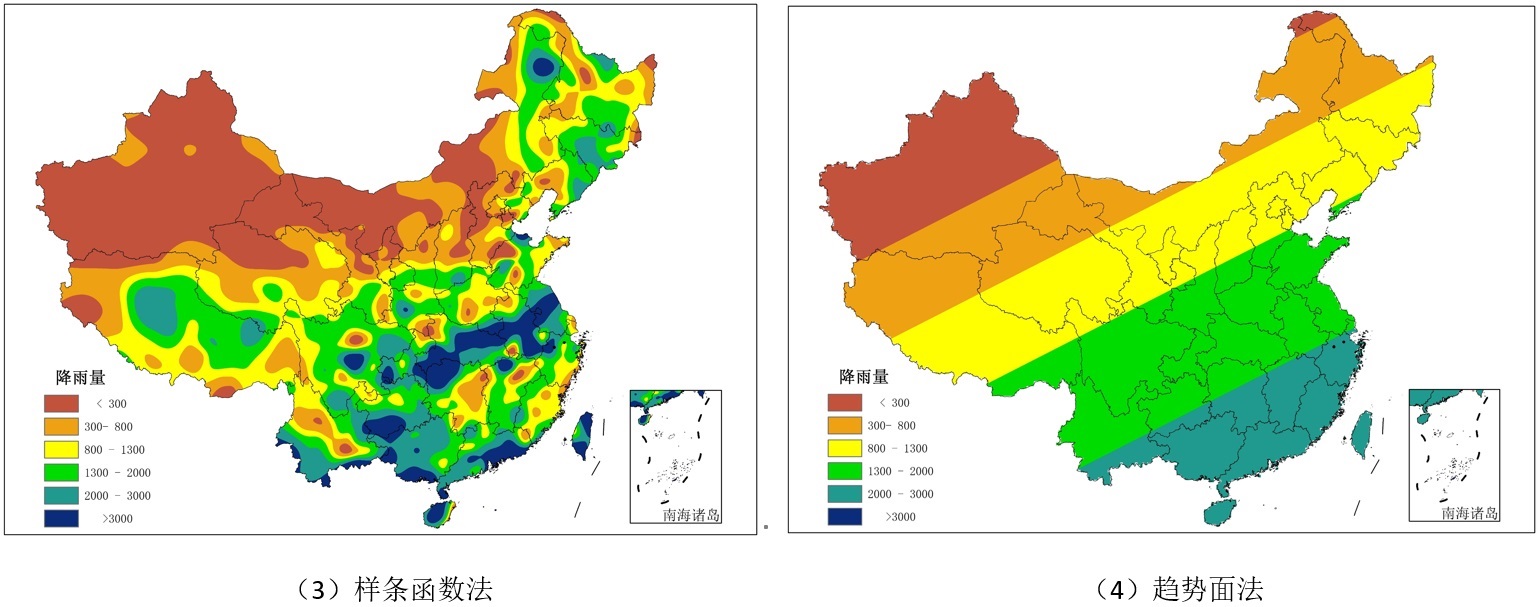
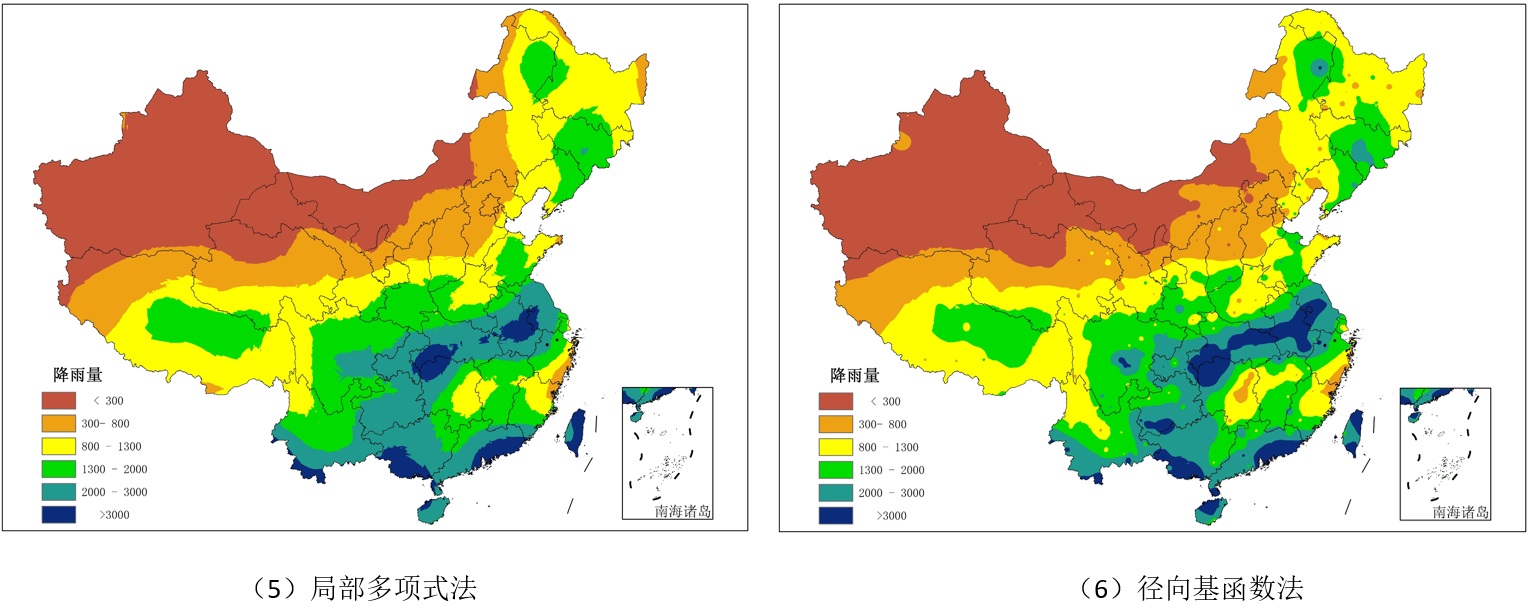
对我国某年6月685个气象站的降水观测数据，采用上述6种方法进行空间插值生成降水表面（图4.83）。
图4.83 不同方法的降水插值结果图
