3.5 空间网络分析
网络是由一系列相互连通、相互作用的点和线等要素组成,用以承载某种资源(物质、能量、信息等)沿着路径在空间上运动的空间要素系统。
网络按其与空间位置是否相关,可以分为空间网络和非空间网络。空间网络也称地理网络,如道路网、河网、电网、供水网、通讯网等,这些都与地理位置相关。然而并非所有与位置相关的网络都可用于空间网络分析,如蜘蛛网、鱼网等。事实上,只有当网络中能够进行物质、能量或信息的传输时,网络分析才具有意义。
空间网络分析是地理信息系统空间分析功能的重要组成部分,其基本思想在于人类活动总是趋向于按一定的目标,选择达到最佳效果的空间位置或寻求资源达到最优配置的解决方案。在GIS中,网络分析是根据点线实体对象之间的拓扑关系来研究构成网络模型的空间实体对象的空间特征和属性特征,进而对网络模型进行全方位的研究和分析的一种空间分析方法。
3.5.1 网络分析基础
3.5.1.1图论基础
图论中的“图”是指由点集合和点与点之间的连线的集合构成的二元组。
点:节点\起始节点\终止节点
边:点与点之间的连线。
相邻与关联:相邻是指相同元素之间的关系,关联是指不同元素之间的关系。
两个端点重合的边称为环。如果有两条边的端点是同一对顶点,则称这两条边为重边。既没有环也没有重边的图,称为简单图。如果图中的边是有向的,则称为有向图,其中的边称为弧。在无向图中,首尾相连的一串边的集合称为路。在有向图中,顺向的首尾相连的一串边的集合叫做有向路。
如果一个图中,任意两个节点之间都存在一个路,则称之为连通图。起点和终点为同一个节点的路称为回路。如果一个连通图中不存在任何回路,则称之为树。任意一个连通图,去掉一些边后形成的树叫做连通图的生成树,一个连通图的生成树可能不止一个。
给定一个图,图中的每一条边赋予一个实数,称这种数为边的权数,这种图称为赋权图。赋以权数的有向图称为赋权有向图,也可称为网络。此外,也可以给网络中的节点赋权。
3.5.1.2空间网络中的基本元素及属性
网络主要由线状目标及其附属的点状目标组成,每种目标又有各自的属性。
1.链
网络中两个节点之间的弧段称为链,它是构成网络模型的最主要的几何框架,对应着图或网络中的各种线状要素,表现的是网络中的地理实体和现象,通常用中心线代表地理实体和现象本身。
链的属性信息有三种:第一种是阻碍强度,即链所耗费的时间、费用等;第二种是资源需求量,即通过该链可以收集的或分配给一个中心的资源总量;第三种是资源流动的约束条件,即表达链自身对资源通行的限制。
2.节点
网络链的两个端点即为网络节点,网络中链与链之间通过节点相连。如果节点参与资源分配,节点也有资源需求量,如节点的方向数。节点也具有是否允许通过的约束能力,如人行天桥规定了其下通行车辆的限高。
3.站点
站点是网络中装载或卸下资源的节点位置,在网络中传输的物质、能量、信息等都是从一个站点出发,到达另一个站点,如车站、码头等。
站点的属性主要有两种:一是站点的资源需求量,表示资源在站上增加或减少,正值表示装载资源,负值表示卸下资源;二是站点的阻碍强度,代表与站有关的费用或阻碍,如某个车站上下车的时间。
4.中心
中心是网络中具有一定的容量,能够从链上获取资源或发送资源的节点所在地。
中心的属性主要有两种:一种是中心的资源总量,它是从其他中心可以流向该中心或从该中心可以流向其他中心的资源总量。另一种属性是阻碍强度,即沿某一路径到达中心所经历的弧段总阻碍强度的最大值,如最大服务半径。
5.障碍
障碍是指对资源传输起阻碍作用的节点或链,它阻碍了资源在与其相连的链间的流动,代表了网络中元素的不可通行状态。如供水网络中的水阀、禁止通行的关口等。
一般认为障碍只是指状态临时设为阻断,不表示任何属性的网络元素,但对于一些元素如交通网络中的交通灯,也可认为是障碍。
6.拐点
拐点是指网络节点处,所有资源流动的可能的转向。拐点描述了网络中相互连接的网络链在节点处的关系,其主要属性是阻碍强度,表示在一个节点处资源流向某一弧段所需要的时间或费用。
7.资源
资源是网络中传输的物质、能量、信息等。资源可能是有形的,也可能是无形的。资源的属性取决于资源本身的种类。
8.权值
权值是用于存储通过一条链或节点时所需要的成本,如链的长度、通过的时间等。权值是可以有方向的,用于交通网络中。权值可能是定值,也可能是动态变化的。权值可能是单一的,也可能是复合的。复合权值可以通过基于特定模型的函数求解。
3.5.1.3网络分析的应用
1.路径分析。
2.资源分配。
3.连通分析。
4.流分析。
5.动态分段。
6.地址匹配。
3.5.2 路径分析
路径分析即是在指定网络的节点间找出最佳路径。最佳路径即是满足某种最优化条件的一条路径。最“佳”的标准有多种,它可能是距离最短、时间最少、费用最小、路线利用率最高,甚至是景观最好、乘车舒适性最佳等。
路径分析的关键是对路径的求解,即如何求出满足条件的最优路径。而最优路径的求解常常可转化为最短路径的求解,最短路径指网络图中一个点对之间,总边权最小的连接起止点的边的序列。若一条弧段的权值表示起始节点和终止节点之间的长度,那么任意两节点之间的各条路径长度就等于该路径上所有边的长度之和,而最短路径就是所有路径中长度最小的路径。最短路径问题是网络分析中的最基本问题,其算法的效率直接影响网络最优化问题的效率。
进行网络路径分析之前,一般需要先将无向的网络转换成加权的有向网络,也就是给网络中的弧段(边、链)等要素赋以权值,其值的大小视约束条件而定。
3.5.2.1 最短路径的数学模型
最短路径的求解首先要把现实世界中的交通、管线等各种网络抽象成一种数学模型,这种抽象出来的数学模型也就是网络的拓扑结构。在数学和计算机科学领域,网络通常抽象为图。对于无向图一般采用邻接矩阵或者邻接多重表来表示,而有向图则可以用邻接表或者十字链表来表示。在建立数学模型的基础上,再利用数学方法求解最短路径。
求解最短路径可以视为一个线性规划问题。求最短路径的问题实际上就是求解上述模型的最优解。
最短路径问题通常有三种情况:一种是求解两个节点之间的最短路径;第二种是求解一个节点到图中其他所有节点的最短路径;第三种是找出图中所有节点对之间的最短路径。根据源点的数量,最短路径的算法分为单源最短路径算法和多源最短路径算法,常用的算法有Dijkstra算法、Floyd算法和A*算法。
3.5.2.2Dijkstra算法
解决最短路径问题的经典方法是E.Dijkstra提出的贪婪算法(Greedy Method),可用于计算一个节点到其他所有节点的加权最短路径。其主要特点是以起始点为中心向外层扩展,直到终点为止。
Dijkstra算法的基本思路是将网络转换成邻接矩阵和有向图,再采用运筹学方法解决最佳路径问题(具体过程略)。
Dijkstra算法是全向搜索方法,不仅可以求一个源点到某一特定终点的最短路径,还可以求源点到其他各点的最短路径,但也由于它遍历计算的节点很多,计算效率偏低。
3.5.2.3 Floyd算法
略
3.5.2.4 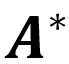 算法
算法
略
3.5.3 资源分配
资源分配的核心就是资源的定位及分配。
资源的定位即是指已知需求,确定在哪里布设最合适的供应点,即寻找最佳的供应点,实质是选址的问题。
资源的分配问题则是确定这些需求源分别受哪个供应点服务的问题。
在实际应用中,这两个问题通常需要同时解决,即在网络中根据需求点的要求,选定合适的供应点和供应方案,同时在网络中选取相应的边和节点,使得在网络覆盖范围内供应点与需求点的关系在一定意义上达到最优,如距离最小、费用最低等。因此,资源分配是网络设施布局、规划中的一个优化问题,其本质是需求点与供应点的优化配置。
许多资源分配问题的供应点布设要求满足多种组合条件,比如在选择供应点时不仅要求使总的加权距离最小,有时还需要使总服务范围最大,有时又限定服务范围最大距离不能超过一定的限值等,这些问题都可以分解为多个单目标问题,利用单目标方程即最小目标值法来求解。所谓目标方程是用数学方式表达满足所有需求点到供应点的加权距离最小的条件方程,也称为P-中心定位问题(P-median location problem),是定位与分配问题的基础。
资源分配常用的模型是P-中心定位与分配模型,它最初由Hakimi于1964年提出。在该模型中,供应点和候选点都位于网络的节点上,弧段则表示可到达供应点的通路或连接,使用的距离是网络上的路径长度,特定的优化条件可以是总距离最小、总时间最少或者总费用最少等。
3.5.4 连通分析
在地理网络中从某一点出发能够到达的全部节点或边有哪些,如何选择对于用户来说成本最小的线路,这是连通分析所要解决的问题。连通分析的求解过程实际上就是对应图生成树的求解过程,其中研究最多的是最小生成树问题。
最小生成树问题在实际生活中的一个典型应用是以给定设施(如学校)的位置为目的地,识别满足一定距离要求的街道线路。例如,某学校选择接送学生的校车行车路线,需要确定哪些学生居住地点距离学校较近而不需享受校车服务,以节省时间和资金投入。
在众多的连通分析求解算法中,比较著名的有Krushal算法和Prim算法。
3.5.5 流分析
地理网络中不断地进行着各式各样的资源,如电力、货物等的流动。如何使资源合理、快速地流动,是网络分析中的重要问题。这样的资源流动问题即是网络中的流分析。流是资源在网络中的传输能力。
网络流分析就是根据网络元素的性质选择将目标经输送系统由一个地点运送至另一个地点的优化方案,网络元素的性质决定了优化的规则。
网络流的最优化问题一直是地理网络研究的一个重要问题,主要涉及两方面内容:网络最大流问题和最小费用流问题。最大流问题指的是一个网络中怎样安排网上的流,使从发点到收点的流量达到最大。在实际应用中,不仅要使网络上的流量达到最大,或达到要求的预定值,而且还要使运送流的费用或代价最小,即解决最小费用问题。
3.5.6 动态分段
动态分段(Dynamic Segmentation)是用于将地理线性要素与现实交通网络中的道路状况、事故等链接起来的动态分析、查询、显示和绘图技术。
动态分段技术在传统GIS数据模型的基础上利用线性参考系统的思想和算法,通过建立一种比“弧段—节点”数据模型更高级的“动态段—动态节点”模型,将属性和它对应的线状要素位置存储为独立的事件属性表(事件表),在分析、显示、查询和输出时,直接依据事件属性表中的距离值对线性要素进行动态逻辑分段,动态地计算出属性数据的空间位置,不必随每个属性集的分段不同来修改对应的二维空间中的x,y坐标数据。
3.5.7 地址匹配
地址匹配(Address Matching),又称地理编码(Geocoding)。简单来说,它是将文字性的描述地址与其空间的地理位置坐标建立起对应关系的过程。具体来讲,它是一种基于空间网络(如路网)的定位技术,它将包含地址的属性数据与GIS系统中具有地理位置的点相连接,从而将其在实际地理空间显示出来。
地址匹配提供了一种把描述成地址的地理位置信息转换成可以被用于GIS系统的地理坐标的方式,通过将只有属性数据的源表中记录了地址的字段与地址数据库中的地理实体的对应字段的属性值进行比较,若找到相匹配的,就将地理实体的地理坐标赋给源表中的记录,从而实现源表中的地理编码。利用地理编码技术,可以建立空间信息与非空间信息之间的联系,使用户能用地址去确定在地图中的对应位置。
要实现地理编码,必须要有两种数据:空间数据和非空间数据,其中空间数据是已经包含了相关地图定位信息的地理参考数据(如街道地图数据),非空间信息数据只包含地理实体的位置信息,而没有相关的地图定位信息的地址数据(如街道的门牌号)。
3.5.8 ArcGIS中的网络分析工具
ArcGIS中有两种网络分析工具,一是传输网络(Network Analyst),二是设施网络(Utility Network Analyst)。两者的区别主要体现在以下三个方面:
1.在地位和作用层面上
传输网络,特别适宜街道、公路、铁路、人行道等交通传输网络的模拟,在ArcGIS中是一个专门用于网络分析的扩展模块。在Arctoolbox中有网络分析工具集(Network Analyst Tools),它提供了一套完整的创建、维护网络数据集和执行网络分析的工具。在ArcMap中,还有专门的传输网络分析工具条Network Analyst来执行网络分析。
设施网络特别适宜水、电、气等管网设施以及河流的连通性等方面的分析,依托于Geodatabase创建几何网络(Geometric Network),采用ArcMap中的Utility 设施网络分析工具条Utility Network Analyst来具体执行网络分析操作。
2.应用层面上
传输网络主要特点在于它是一种无方向网络,它把汽车、火车等传输工具看作是可以自由移动的物体,有主观选择方向的能力。网络中还可以设置限定性规则。它主要解决以下问题:1)计算点与点之间的最佳路径。2)可以进行多点的物流派送物。3)寻找最近的一个或者多个设施点。4)确定一个或者多个设施点的服务区。5)绘制起点-终点(Original-Destination,OD)的成本矩阵。
设施网络的主要特点在于它是有向网络,即网络中流动的资源要完全遵照已经设定好的网络规则进行运动,自身不能决定流向。它主要解决寻找连通的或不连通的管线、上/下游追踪、寻找环路、寻找通路、爆管分析等网络问题。
3.技术层面上
传输网络基于网络数据集(Network Dataset),设施网络基于几何网络(Geometric Network).
Network Dataset 需要采用Arctoolbox中有网络分析工具集(Network Analyst Tools)来创建,而几何网络(Geometric Network)则需要在Geodatabase的要素数据集(feature dataset)中创建。



