距离反映要素之间的空间接近程度,是空间分析的一个重要指标。
距离可以通过矢量数据中的道路网络来计算,也可以通过栅格数据中像元之间的相互连接来计算。
基于栅格的距离计算有三种类型:
直线距离:或称自然距离、欧氏距离,不考虑点(像元)与点(像元)之外的任何情况,只考虑两点各自当前的位置。
成本距离:考虑相邻像元之间的连通距离与难度(成本),通过累积成本最低的像元间联系线路来确定距离。
路径距离:在成本距离的基础上,还考虑表面距离、垂直因子和水平因子的影响。
4.3 距离分析
4.3.1 自然距离
自然距离(Nature distance),也称直线距离(Straight-line distance)、欧几里德(欧氏)距离(Euclidean distance),它测量的是从一个像元中心至另一个像元中心在欧氏平面上的直线距离。
自然距离可以采取两种方式进行计算。一是基于像元坐标来计算。二是基于行列数来计算。
距离分析必须基于源(Source)。源是距离分析中的目标或起点(Distance to 或Assign to),在空间上它是一些相互离散的点、线或面,如学校、银行、道路、公园等。源可以采用栅格数据,也可以采用矢量数据,但在运算前需要转换为栅格数据。源往往不只一个,距离的计算实际上是求取每一栅格像元至与其最近的源的距离。
当自然距离栅格数据采用分级显示时,它十分类似于矢量数据的多级缓冲区。
距离分析中,除了计算距离本身外,往往还需要进行区域配置(Allocation)及方向(Direction)的计算。
区域配置确定每一个像元属于哪一个最近源,像元值与所对应的源相同。它的实质是确定至各个源最近的区域,类似于泰森多边形。
方向栅格中的像元值为该像元至最近源的方向。方向值常以度为单位,以正北为起点顺时针从0°至360°。
自然距离只考虑空间要素或现象之间的距离本身,而不考虑地表特性,因此在实际应用中,自然距离往往很受限制。

自然距离分析示意图
4.3.2 成本距离
4.3.2.1 成本与成本栅格
成本距离(Costdistance)也称耗费距离。它的基本思想是,地理事象的移动,不仅与距离本身有关,还与地面本身的特性有关。这些地面特性直接影响通过该像元的开销,即成本。
成本距离分析需要有成本栅格数据。该数据中的像元值是指对某一分析目标而言通过该像元所需要的成本。这种成本可以是金钱、时间等常用的物理量,也可以是一些不具特定意义的综合性评价指标,它往往用于成本受多因素影响的情况,其成本栅格数据中,每一个像元的成本往往都是几种不同成本被赋予不同的权重值后相乘再相加所得到的结果。
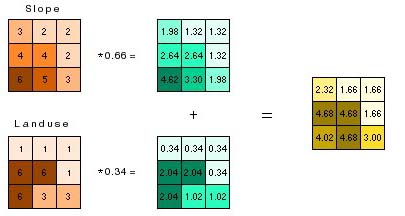
成本栅格的计算示意图
4.3.2.2 成本距离加权
成本距离加权计算的是每一个像元到距离最近、成本最低的源的最少累计成本(Accumulative Cost)。
累计成本必须考虑相邻像元之间的连接路径。横向或纵向连接的相邻2个像元之间的成本距离为它们成本的平均值;斜向连接的相邻像元间的成本距离是平均成本乘以1.4142。
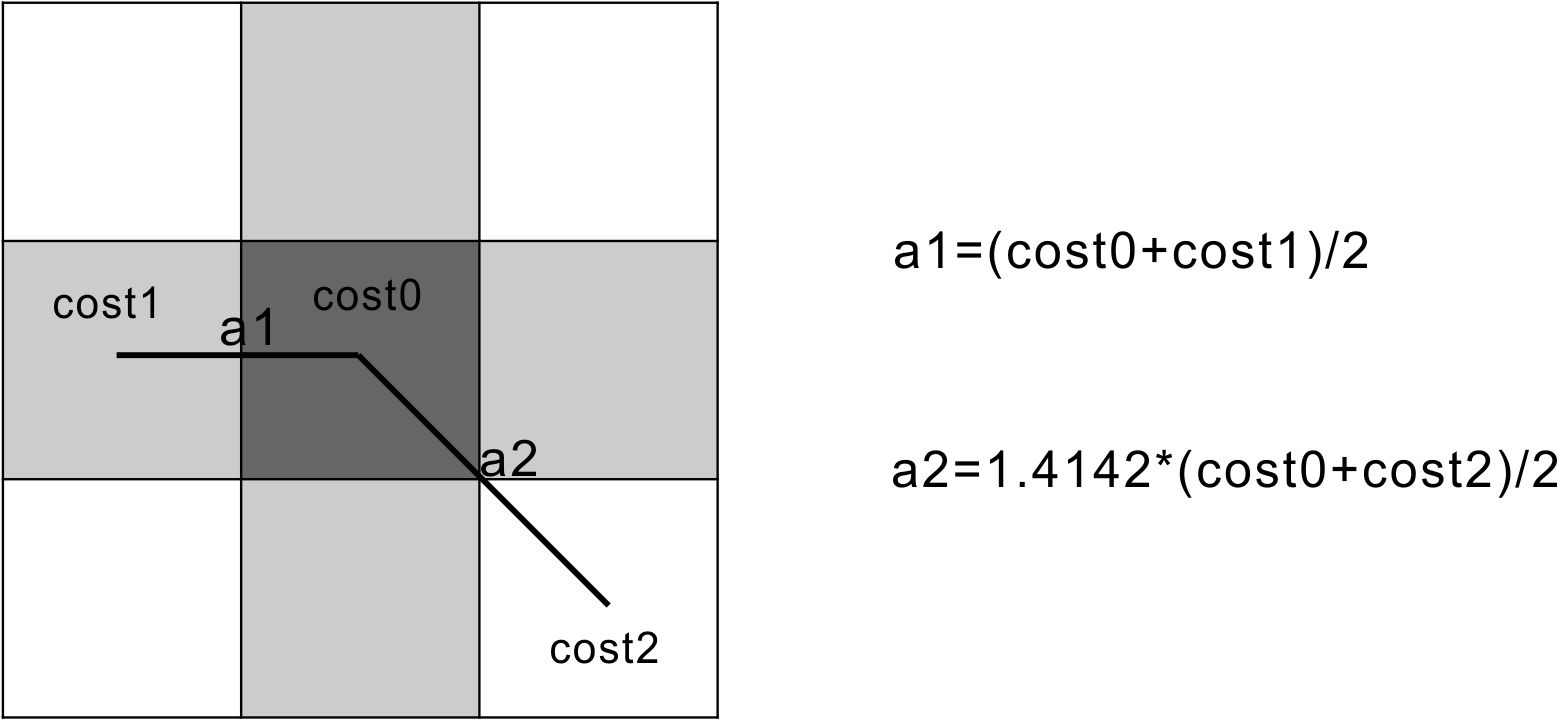
不同连接路径的成本距离
图4.67a是一个具有两个源的栅格数据,图4.67b是该区域的成本栅格数据。根据这两个数据计算累计最小成本栅格,需要一个基于Diijkstra算法的从源像元开始的迭代过程,其基本步骤如下(图4.67):
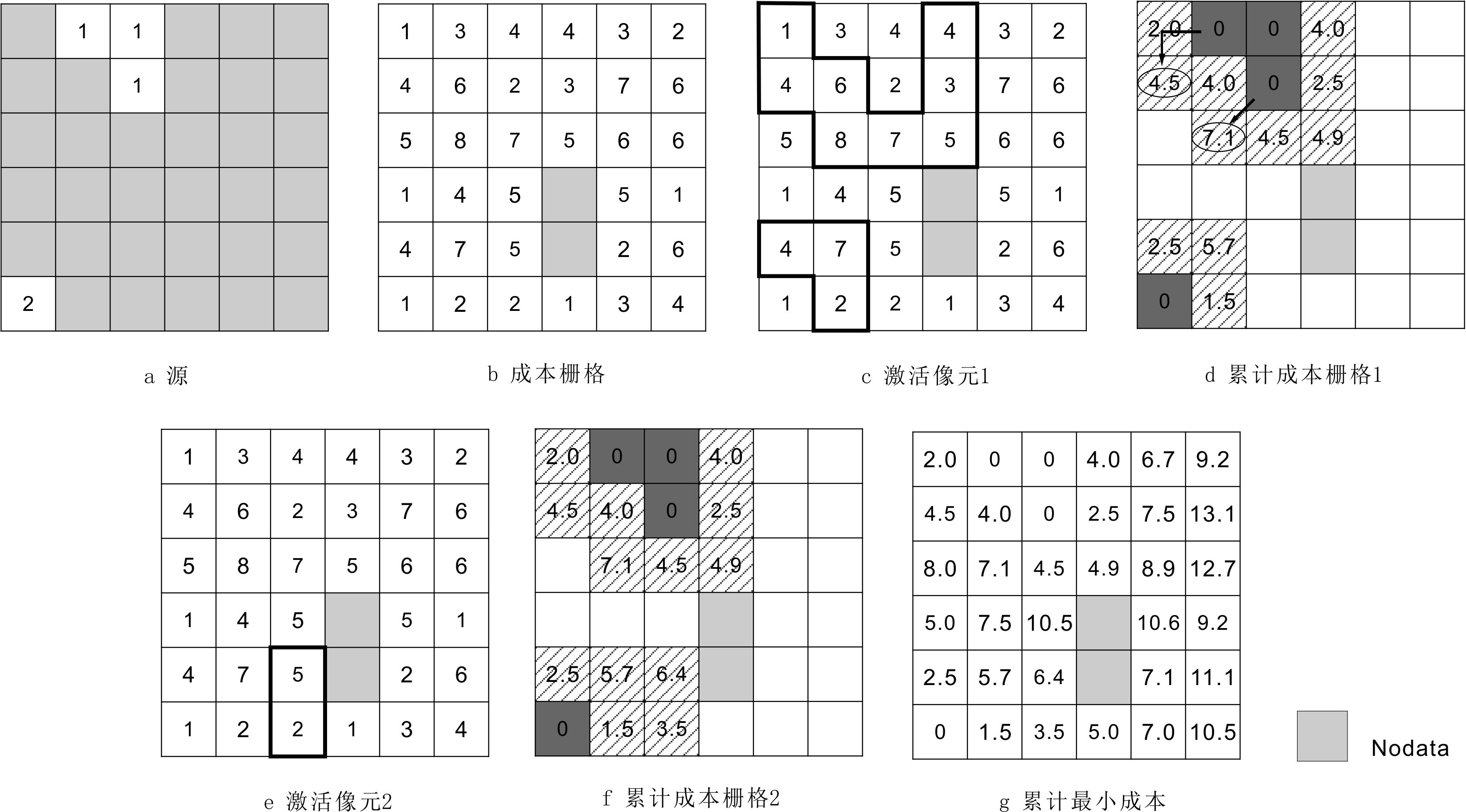
图4.67累积最小成本的计算过程
步骤1:将源像元的累计成本赋值为0,并激活与源像元相邻接的像元,组成累计成本活动像元集(图4.67c中粗线框里的像元),根据连接状况及其成本计算方法,计算每个活动像元的最低累计成本值。
步骤2:选出上一步活动像元集中累计成本值最小(1.5)的像元,先将其值赋予输出的成本栅格数据中同位置的像元,并将它从活动像元集中剔除,再将它的相邻像元(图4.67e中粗线框里的像元5、2)补充进入活动像元集中,计算其最低累计成本(图4.67f)。
步骤3:重复第2步,不断进行循环迭代,直至所有的像元均已赋予最低累计成本值(图4.67g)。
4.3.2.3 成本方向与成本配置
成本方向(CostDirection,Cost Back Link):根据累积最低成本栅格数据,确定每一个像元沿最低成本路径,回到最近邻源的方向。
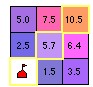
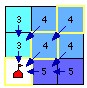
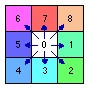
加权成本 成本方向 方向编码
成本方向数据说明图
成本分配(CostAllocation):基于最低累计成本,确定每一个像元属于哪一个最近源,像元值与所对应的源相同。
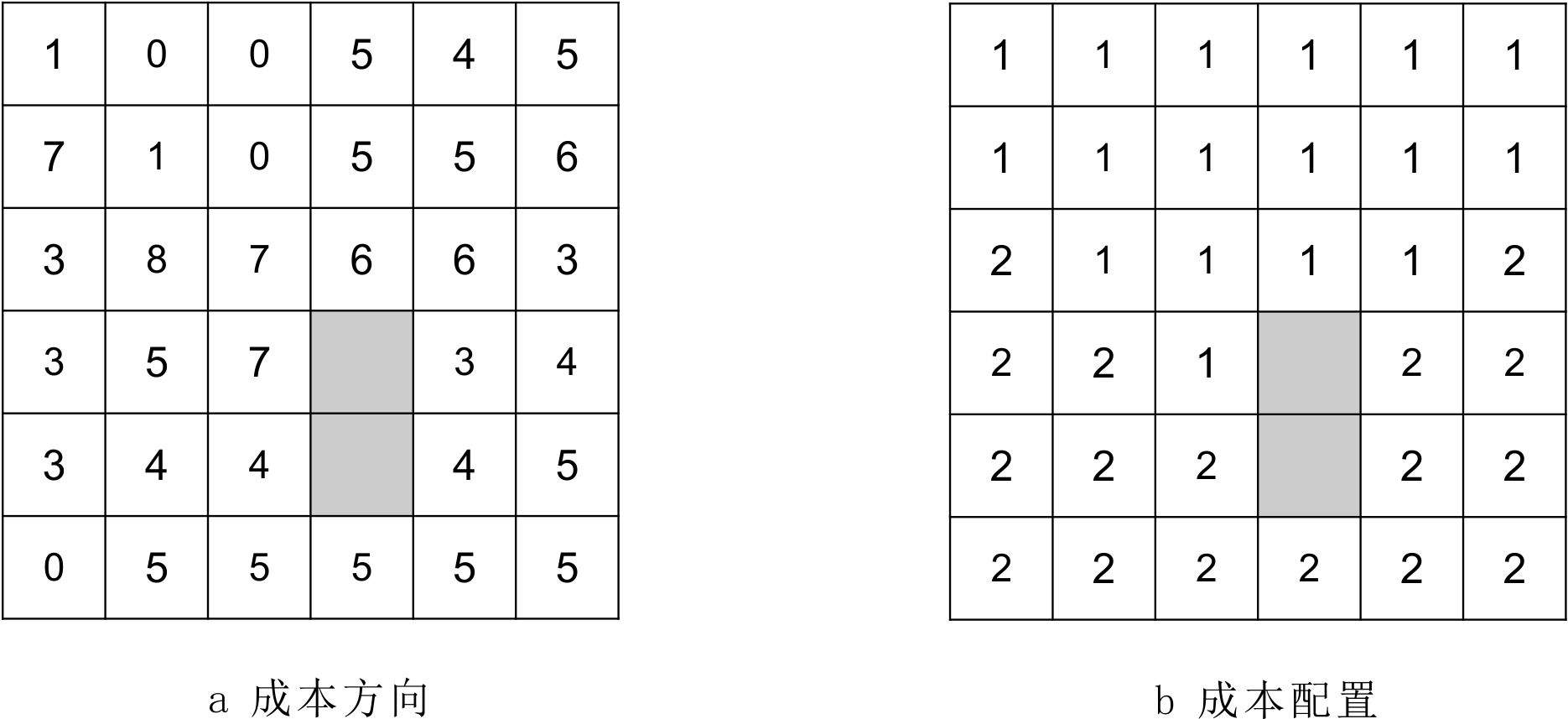
成本方向与成本配置
4.3.2.4 成本路径
成本路径(Costpath):计算从指定目标(destination)出发,到达累计成本最低的源的路径。目标数据可以是点、线、面等矢量要素,也可以是栅格数据。ArcGIS中提供了三种最低成本路径算法:
1.Each Cell:为目标数据中每个像元寻找一条成本最小的路径。
2.Each Zone:为每个目标数据寻找一条成本最小的路径,同一目标中所有像元共享同一条路径。
3.Best Single:为所有目标寻找一条成本最小的路径,只有一个目标与一个累计成本最低的源相连。
成本距离分析常常用于选址分析、路径分析等应用之中。例如,学校、连锁商场、银行网点的合理布设、购物中心的选择、公路规划选线、旅游线路的设计、事故救援路线的确定等。
4.3.3 路径距离
路径距离(Pathdistance)是对成本距离的改进,涉及三个新的变量:一是表面距离。它可以由DEM生成,用于量测从一个像元至另一个像元所经过的地面实际距离。像元之间高差或坡度越大,其表面距离也越大。因此表面距离能够比平面距离更真实地反映相邻像元之间的距离关系。二是垂直因子。它决定了像元间移动要克服垂直因素(如上坡和下坡)的难易程度。三是水平因子。它决定了像元间移动要克服水平因素(如侧风)的难易程度。
ArcGIS中的路径距离工具,采用了表面距离、垂直因子和水平因子三个参数来改进成本距离。
对于直边的4个相邻像元来说,其与中心像元的成本距离采用以下方式计算(a、b为相邻像元):成本距离={[(成本a×水平因子a)+(成本b×水平因子b)]/2}×表面距离ab×垂直因子ab。
对于斜角的4个相邻像元来说:成本距离={[(成本a×水平因子a)+(成本b×水平因子b)]/2}×1.4142×表面距离ab×垂直因子ab。
路径距离分析可以认为是成本距离分析的升级,它改进了成本距离的计算方式,其成本累计过程与成本距离分析中的类似。与成本距离分析一样,路径距离分析也可以计算方向数据(Path distance backlink)与配置数据(Path distance allocation)。












