2.3 空间数据的结构
空间数据结构(SpatialData Structure)是指适合于计算机存储、管理和处理的,用于表达和描述空间对象的数据的逻辑结构。
主要有矢量数据(Vector)、栅格数据(Raster)及不规则三角形网(TIN)等几种基本的数据结构。
2.3.1 矢量数据结构
矢量(Vector)数据结构是利用欧几里得(Euclid)几何学中的点、线、面及其组合体来表示现实世界中地理实体或现象的空间分布,通过记录空间对象的坐标及空间关系来表达空间对象的位置的数据结构。
简单数据结构:又称面条(Spaghetti)结构,是指只以基本的空间对象(点、线、多边形)为单元进行单独组织,记录空间对象的位置坐标和属性信息,不记录拓扑关系的一种矢量数据结构。主要特点是:(1)数据按点、线或多边形为单元进行组织,数据结构直观简单。(2)每个多边形都以闭合线段的形式存储,多边形的公共边界被数字化两次和存储两次,容易造成数据冗余和公共边的不一致。当对公共边进行修改时,需要对相邻的多边形也进行修改。(3)点、线和多边形有各自的坐标数据,但没有拓扑数据,彼此互不关联,这在处理如水管与水阀、电线与开关等之间的关联关系时存在问题。(4)岛或洞只作为一个单独的图形,与外界多边形没有联系。
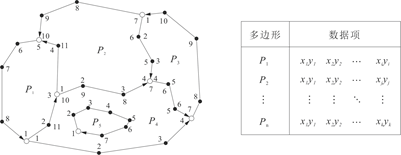
图2.18 简单矢量数据结构
拓扑数据结构:拓扑(Topology)是对空间结构关系进行明确定义的数学方法,具有拓扑关系的矢量数据结构就是拓扑数据结构。它包括索引式数据结构、双重独立编码结构和链状双重独立编码结构等。其共同的特点是:(1)点是相对独立的,点连成线,线构成面。(2)每条线始于起始结点,止于终止结点,并与左右多边形相邻接。(3)构成多边形的线又称为弧段,两条以上的弧段相交的点称为结点。(4)由一条弧段组成的多边形称为岛或洞。不含岛的多边形称为简单多边形,含岛的多边形称为复合多边形。在复合多边形中含有外边界和内边界,岛看做是复合多边形的内边界。
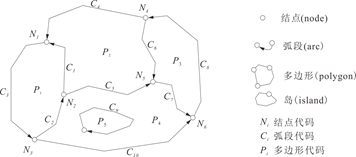
图2.19矢量拓扑数据结构
(1)拓扑邻接关系:反映同类空间图形元素之间的邻接关系。
(2)拓扑关联关系:反映不同类别的空间图形元素之间的关联关系。
(3)拓扑包含关系:反映同类但不同级别的空间图形元素之间的包含关系。
2.3.2 栅格数据结构
栅格(Raster)数据结构用规则排列的像元阵列来表达空间要素的位置和属性。
像元可具有不同的形状,如正方形、长方形,甚至正六边形。为了使用方便,一般采用正方形的像元。
像元的中心表示要素所在的位置。
像元的值代表其所在空间位置的某些属性,例如地物类型、温度、降水、高程、光谱值等。
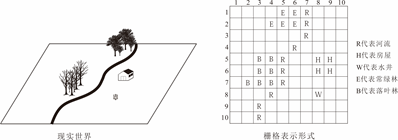
图2.20 栅格数据结构
栅格数据结构中,像元的大小是一个非常关键的指标,它直接影响着空间数据在位置、属性等方面的精度,同时也影响着数据处理的时间和存储的空间。
像元大小代表数据的空间分辨率,决定了栅格所表示的内容的详细程度。理论上,处理时间和存储空间会随像元的变小而成几何级数的增加。
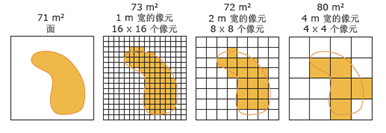
图2.21 栅格数据的不同空间分辨率
像元大小的确定需要考虑以下几个方面的因素:
1.输入数据的精度。
2.应用目标的精度要求。
3.期望的响应时间。即计算所需要的时间。
4.结果数据库的大小与磁盘容量。
5.要注意空间数据的尺度效应。
2.3.3 不规则三角网
不规则三角网(TriangulatedIrregular Network,TIN)是通过将一系列点组成若干个三角形,形成一个相互连接的三角形网络,并由此拟合地表或其他不规则表面的一种空间数据结构。
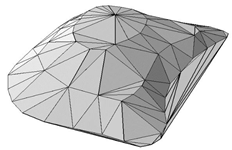
图2.22 TIN数据结构
三角形大小随点的密度变化而变化,所以在表面起伏变化较大或需要更多细节的区域,TIN可具有较高的分辨率,而在表面起伏变化较小的区域,则可具有较低的分辨率。
2.3.4 不同数据结构的对比与应用
数据结构对比:
表2.5 矢量数据结构与栅格数据结构的比较
| 优点 | 缺点 |
| 矢量 | 1.数据结构紧凑、冗余度低
2.有利于网络和检索分析
3.图形显示质量好、精度高 | 1.数据结构较复杂
2.软件实现的技术要求比较高
3.多边形叠合等分析比较困难 |
| 栅格 | 1.数据结构简单
2.便于空间分析和地表模拟
3.有利于遥感数据的匹配应用和分析
4.现势性较强 | 1.数据量较大,冗余度高,需要压缩处理
2.定位精度比矢量低
3.拓扑关系难以表达
|
数据结构的选择策略:根据应用的要求以及数据的特征合理选择不同结构的空间数据。
从技术层面上看,栅格数据在空间叠加分析、空间数据共享等方面比矢量数据更有优势,而矢量数据在网络分析、数据存储、数据精度等方面比栅格数据更有优势。因此一般来说,研究区域为空间尺度较大的自然资源分布、农业区分布、林业区分布等,使用栅格数据结构比较合适,而研究区域为空间尺度较小的城市分区或详细规划、土地管理、公用事业管理等方面,使用矢量数据结构比较合适。
从应用层面上看,数据采集时采用矢量数据结构,有利于保证空间实体的几何精度和拓扑特性的描述;而空间分析则主要采用栅格数据结构,有利于加快系统数据的运行速度和分析应用的进程。
因此,在空间分析前的数据处理阶段,经常要进行两种数据结构间的相互转换。
矢量数据的应用案例:
1.矢量数据用于土地管理
2.矢量数据用于网络构建
3.矢量数据用于专题制图
栅格数据的应用案例:
1.将栅格数据用作底图
2.将栅格数据用于表面地图
3.将栅格数据用作专题地图
2.3.5 数据结构的转换
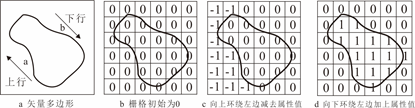
2.3.5.1 矢量结构向栅格结构转换
1.点的栅格化
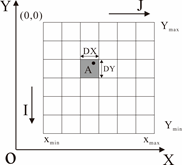
2.线的栅格化
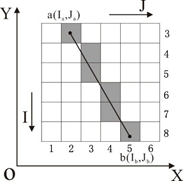
3.面的栅格化
(1)内部点扩散算法
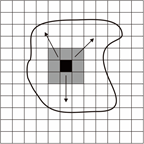
(2)射线算法
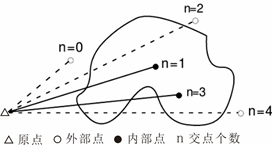
(3)扫描算法
(4)边界代数算法(BAF,Boundary Algebra Filling)
4.ArcGIS中矢量转栅格的工具
(1)点转栅格工具
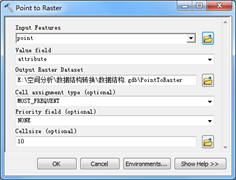
图2.32 Point toRaster工具
Point toRaster中的像元赋值方法:
1)频率最高(MOST_FREQUENT):用户还可设置优先字段(Priorityfield)。优先级相同时,考虑频率最高;频率又相同时,再考虑FID最小。
2)求和(SUM)
3)平均值(MEAN)
4)标准差(STANDARD_DEVIATION)
5)最大值(MAXIMUM)
6)最小值(MINIMUM)
7)范围(RANGE)
8)数量(COUNT)
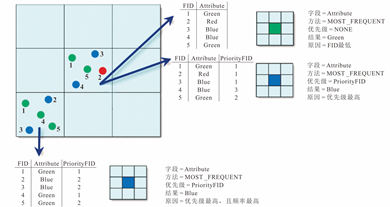
图2.33 Point toRaster栅格像元属性的决定方式
(2)线转栅格工具
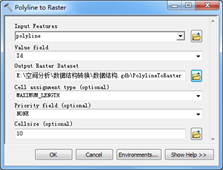
图2.34 Polyline toRaster工具
像元赋值方法:
1)最长(MAXIMUM_LENGTH)。
2)合并最长(MAXIMUM_COMBINED_LENGTH)
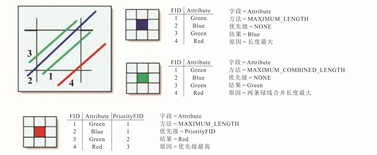
图2.35Polyline to Raster的栅格像元属性决定方式
(3)面转栅格工具
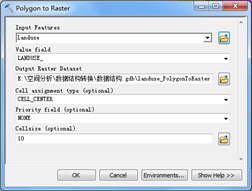
图2.36 Polygon toRaster工具
像元赋值方法:
1)像元中心(CELL_CENTER)
2)面积最大(MAXIMUM_AREA)
3)合并面积最大(MAXIMUM_COMBINED_AREA)
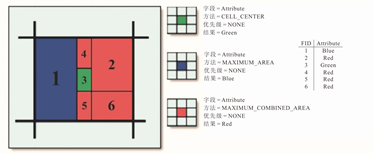
图2.37 Polygon toRaster的栅格像元属性决定方式
(4)要素转栅格工具Feature to Raster
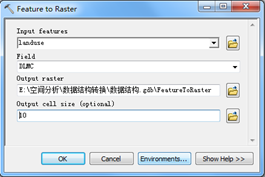
图2.38 Feature toRaster工具
2.3.5.2 栅格结构向矢量结构转换
1.点的矢量化
2.线的矢量化
3.面的矢量化
1)多边形边界提取
2)边界线追踪
3)拓扑关系生成
4)去除多余点及曲线圆滑
4.ArcGIS中栅格转矢量的工具
(1)栅格转点工具Raster to Point
(2)栅格转线工具Raster to Polyline
(3)栅格转多边形工具 Raster to Polygon(注意多边形的简化处理)





















