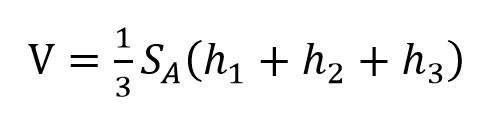3.1 空间量算分析
3.1.1 空间位置量算
3.1.1.1 位置量算
空间位置量算就是对这些点、线、面、体等目标要素的绝对位置或相对位置进行量算。
对于点状要素,其位置主要用坐标来量算。
对于线状要素,其位置用坐标串表达。
对于面状要素,其位置由生成面的边界线的位置坐标来确定;此外,面的质心常常用来说明面状要素作为一个整体所在的位置。
对于体状要素,它存在于三维空间中,可视为由线状要素和面状要素组合而成,因此其位置由围成它的线状要素和面状要素的位置坐标来表达。
空间要素的绝对位置既可以采用以经纬网为基础定义在地球参考椭球体上的位置来表达,也可以采用在某一投影系统下建立的平面直角坐标体系中的位置来描述。
空间要素的相对位置包括距离和方向两个方面。距离的量算采用长度的量算方法。方向的计算通常是以正北方向为起始,并沿着顺时针方向进行的。通常采用两间的坐标来计算长度和方向。
3.1.1.2 质心量算
质心(Center of mass)是地理要素保持均匀分布的平衡点,是描述地理要素空间位置的重要指标之一,通常定义为一个要素或要素群体的几何中心(Centroid)。
对于单个的点要素,其质心在点本身位置上;
对于线状要素,质心就是线的中点;
对于面状要素,质心可理解为多边形的质量平衡点。物理学中,物体的质心可以采用多点悬挂法,通过悬线的交点确定质心位置。数学上,一般采用物体所有质点向量的加权平均模型,通过积分的方式进行计算。
质心不一定位于面要素内。而对于凹状面要素,质心可能在其外部。
对于多个要素,例如要素数据集中的点群、多个线要素、多个面要素等,其质心可采用加权平均模型进行计算。权重的选择可根据实际情况而定。例如,在求区域城市人口质心时可用城市人口数量作为权重;在求取各类土地的分布质心时,可以采用各地块的面积作为权重。
不同类型要素的质心计算可以用于分析要素的空间分布格局。
同一要素不同时间的质心计算可以用于分析该要素的时空动态变化
3.1.2 长度量算
3.1.2.1 线的长度
将线分割为无数个折线段,通过计算每个折线段的长度然后累计得出线状要素的总长度
3.1.2.2 面的周长
周长即为组成多边形的弧段长度之和。量算时,只需要先求出每一条弧段的长度,然后再进行累加即可。
3.1.2.3 距离
1.点与点之间的距离:采用两点间的距离公式进行计算。
2.点与线之间的距离:点状要素与线状要素上的节点和线段之间的距离的最小值。
当点P在直线段AB两端点之间时(即点P到直线段AB的垂足P_0位于AB之间),点P到直线段AB的最短距离为垂距;如果点P在两端点的外侧(即垂足在直线段AB的延长线上),则最短距离即为点P到两个端点A、B中最近的那个端点的值。
点到包含多条折线段的线状要素的距离,可先求算点到各条折线段的最短距离,然后再进行比较,取其中的最小值作为点到该线状要素的最近距离。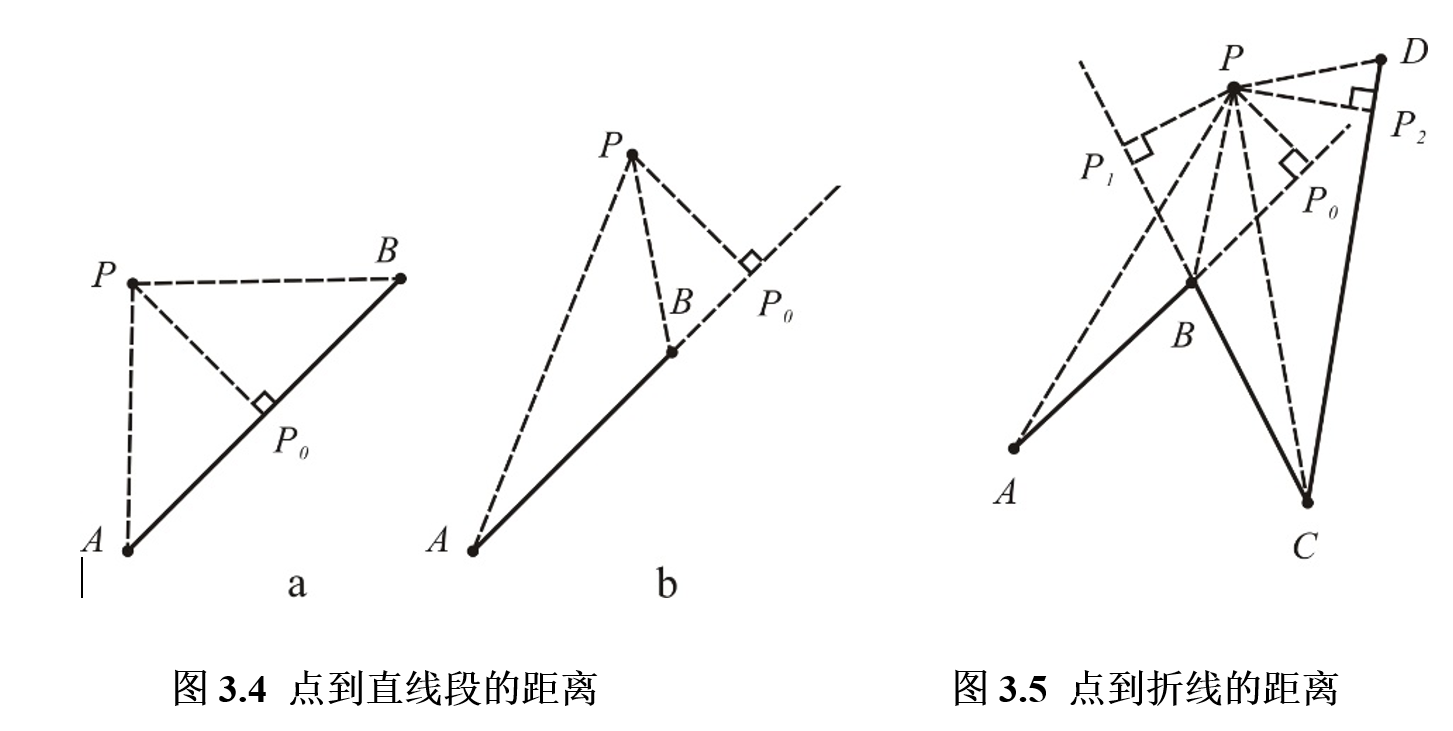
3.点与面之间的距离
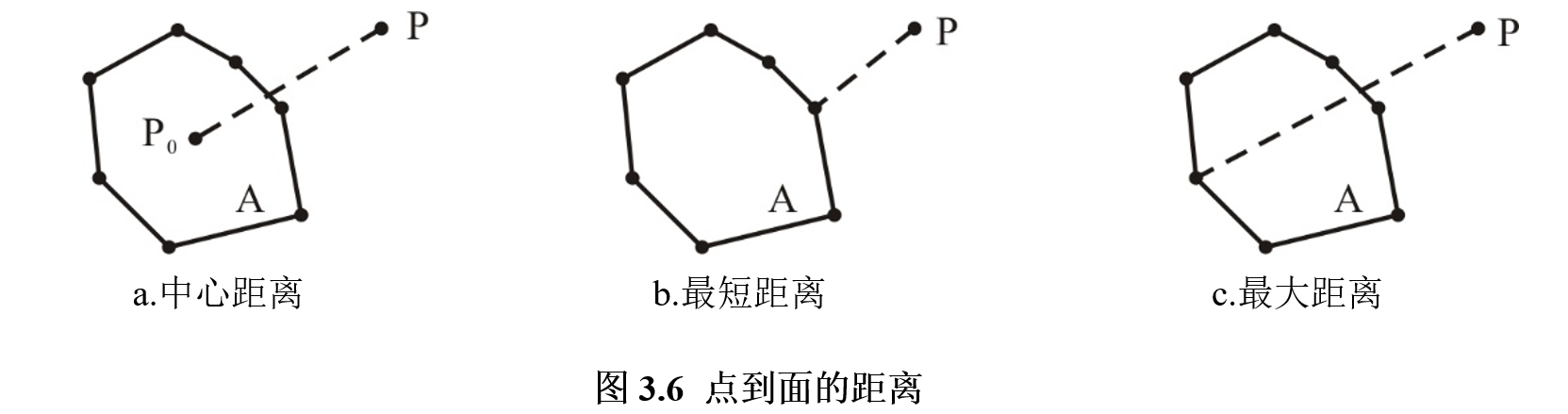
①中心距离。即点P到面状要素A中某一中心点P_0(常采用质心点)的距离。
②最短距离。即点P与面状要素A中所有点之间的距离的最小值。
③最大距离。即点P到面状要素A中所有点之间距离的最大值。
4.线与线之间的距离
线与线相交时,线之间距离为0。
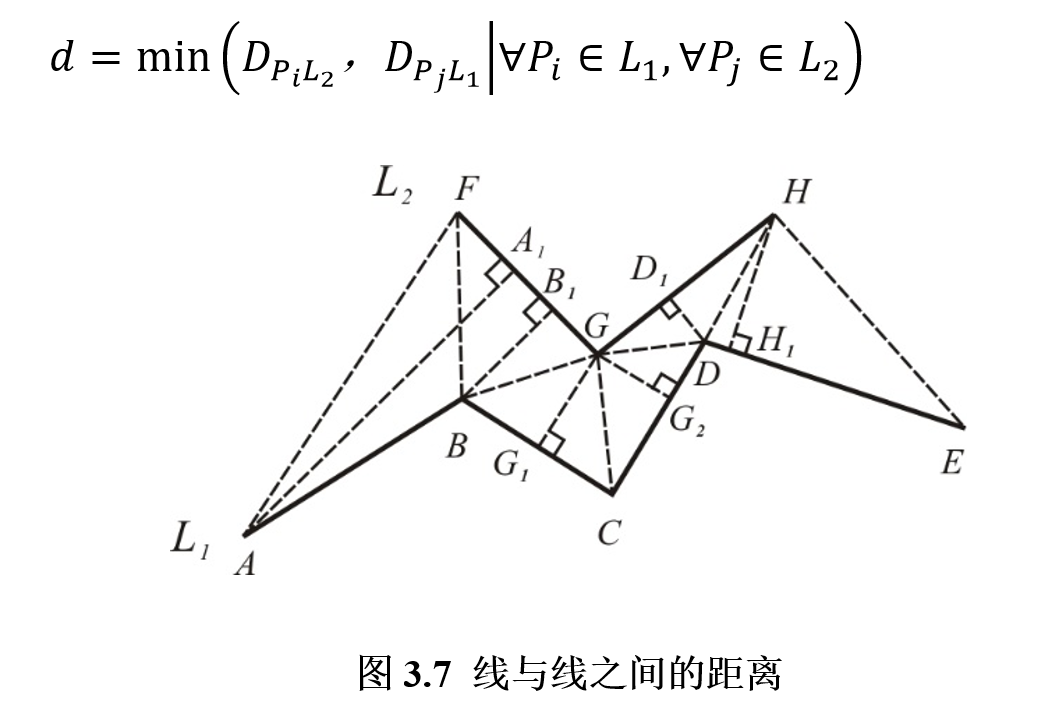
线与线不相交时,线L1和线L2之间的距离定义以下两者的最小值:①D(Pi,L2 ),即L1上的点Pi到L2的最小距离;②D(Pj,L1 ),即L2上的点Pj到与L1的最小距离。
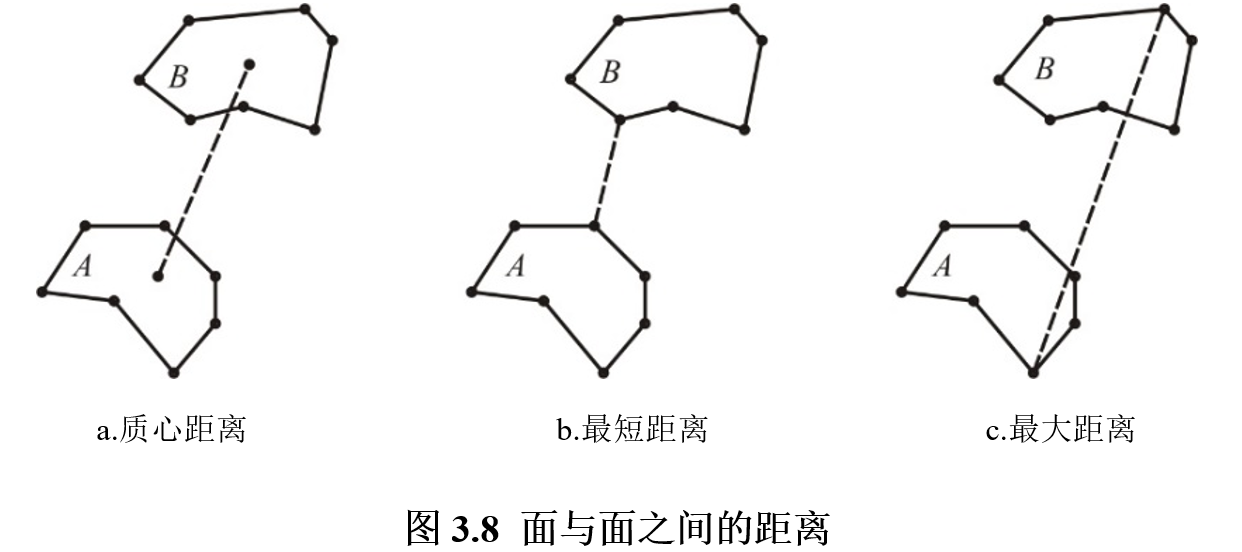
5.面与面之间的距离
①质心距离。两个面状要素质心间的距离。
②最短距离。两个面状要素间最接近的点之间的距离。
③最大距离。两个面状要素间最远的点之间的距离。
3.1.3 面积量算
3.1.3.1平面面积
几何交叉处理法:即过多边形的每个顶点做与x轴的垂线,然后计算各条边、过该边的两个顶点的垂线,以及这两条垂线所截得的x轴部分所包围的面积,最后得到的面积代数和即为该多边形的面积。
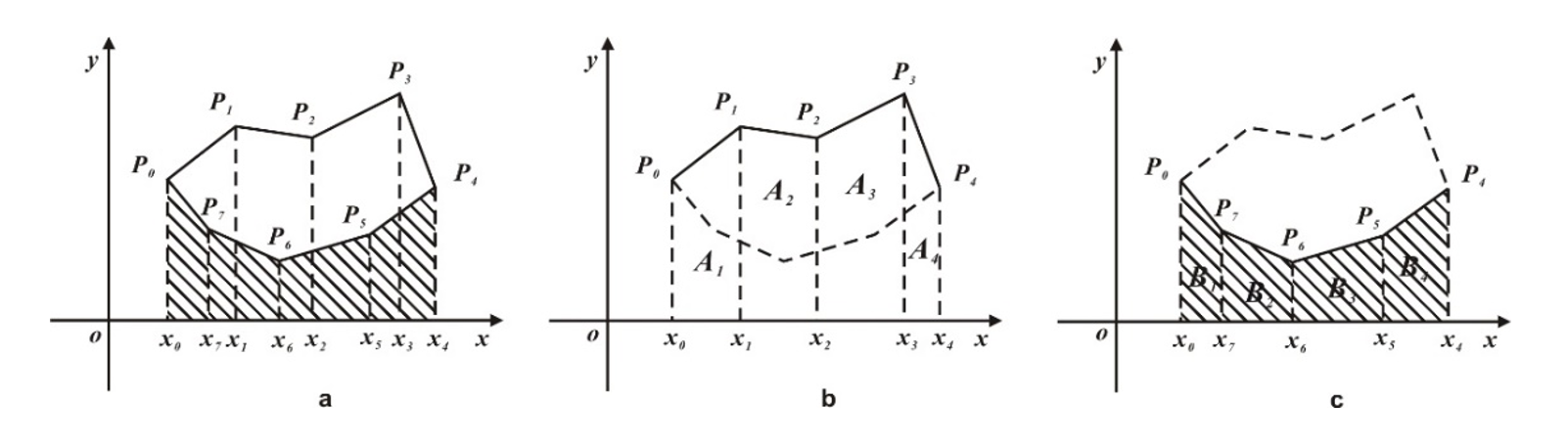
图3.9 几何交叉法平面面积量算
3.1.3.2表面面积
1.基于三角形格网的表面积计算
海伦公式: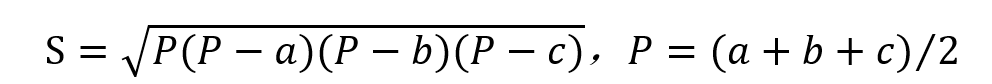
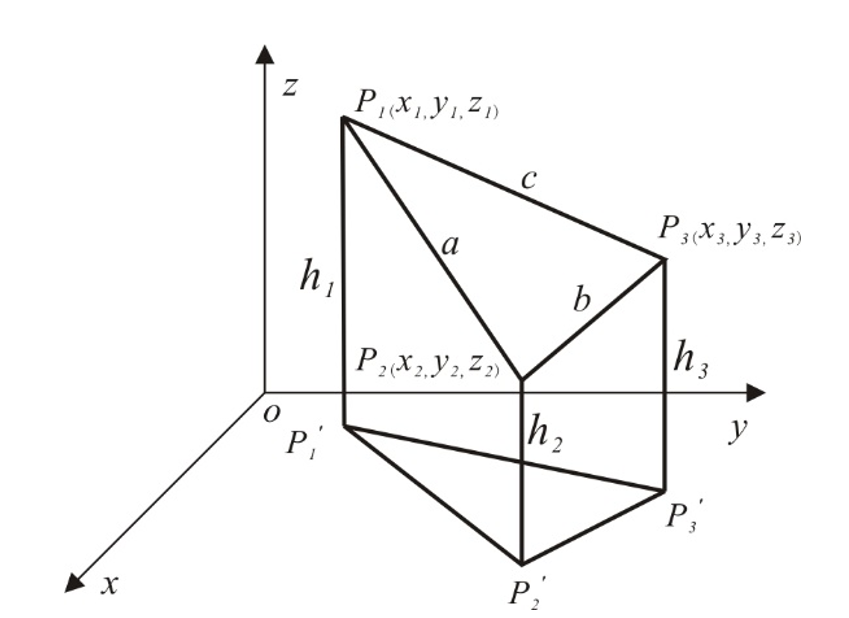
图3.10 三角形格网表面积计算
2.基于正方形格网的表面积计算
简便的近似方法:将正方形格网对角划分为两个三角形格网,然后利用三角形格网的表面积公式进行计算。
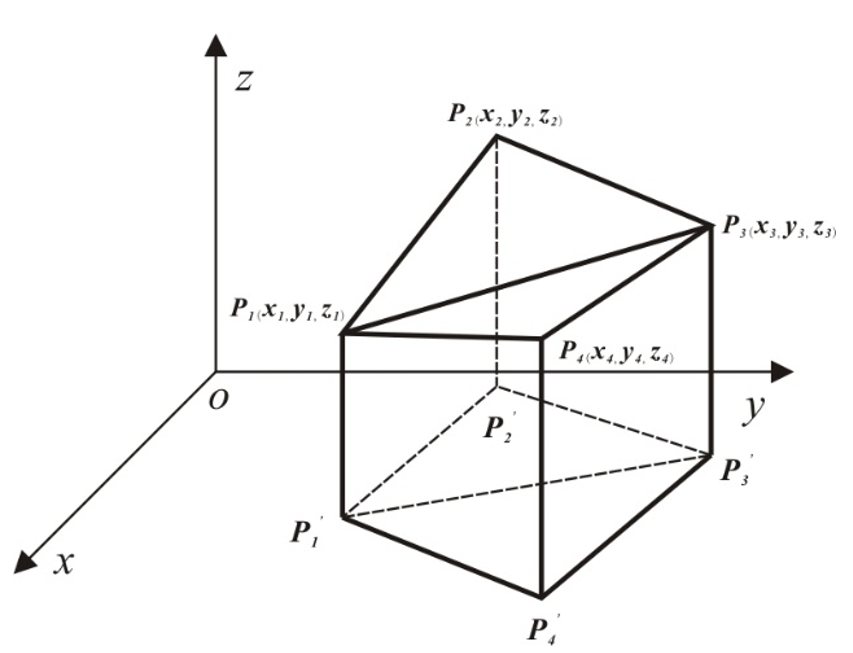
图3.11 正方形格网转为三角形格网进行表面积计算
3.1.4 体积量算
1.基于等高线的体积量算
将不规则体分割为若干规则体,然后套用基本公式计算规则体的体积,最后累加各规则体的体积得到总体积。
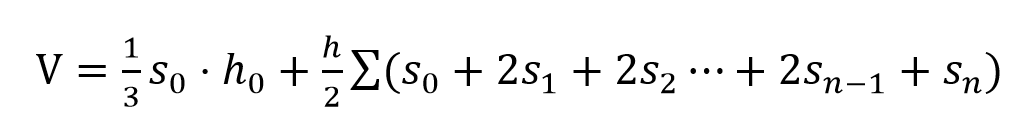
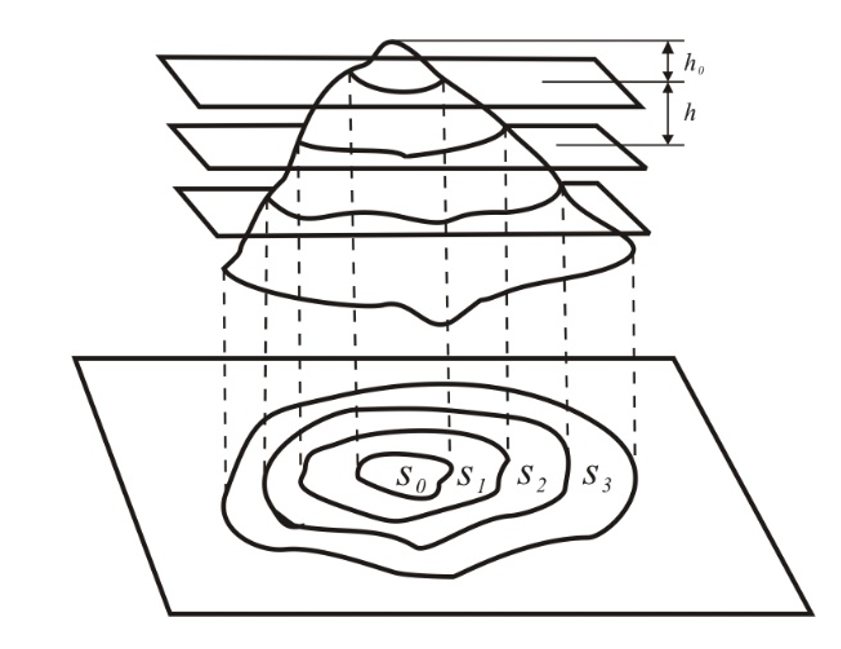
图3.12 基于等高线的体积量算
2.基于TIN的体积量算
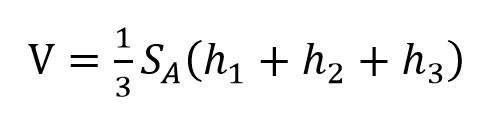
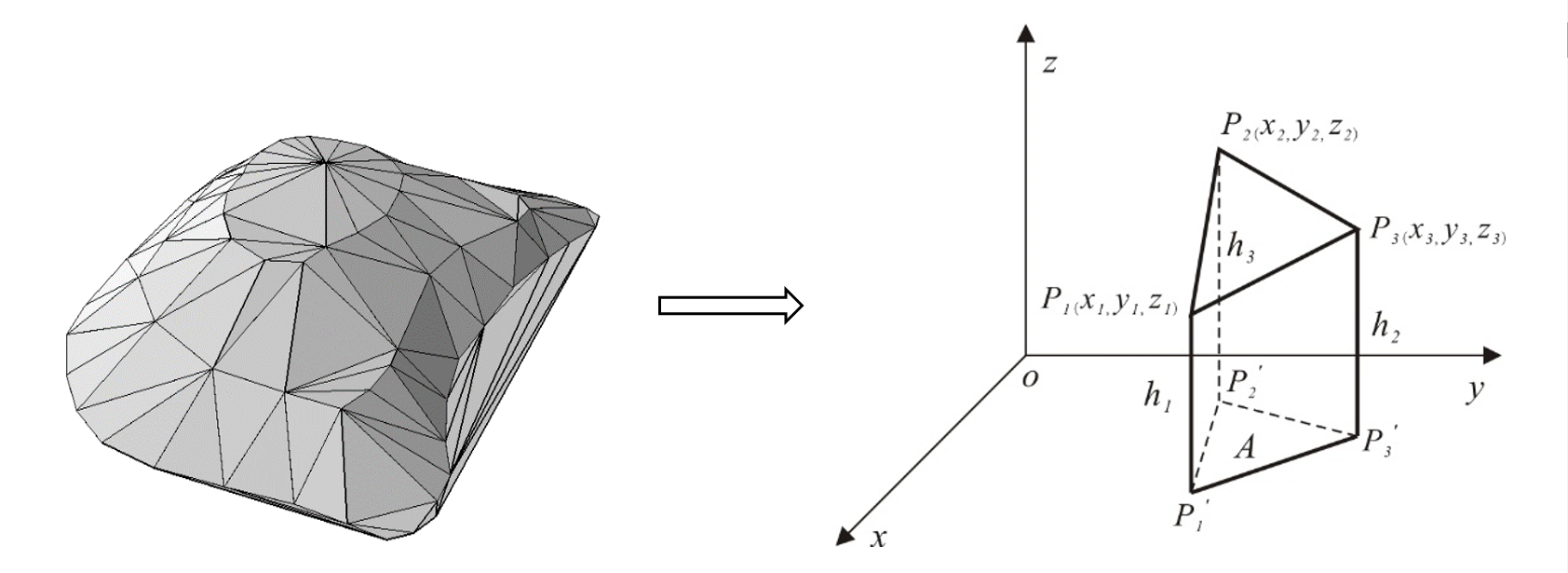
图3.13 基于三角形格网的体积量算
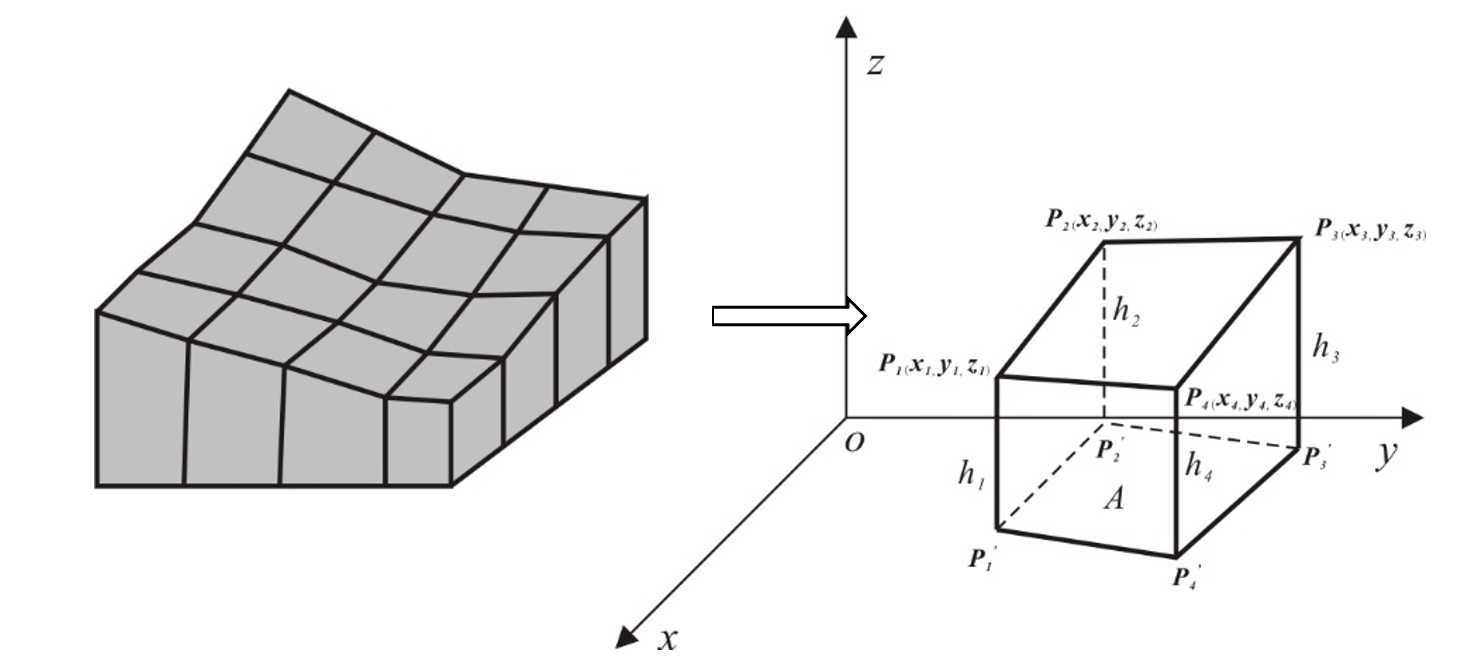
2.基于正方形格网的体积计算
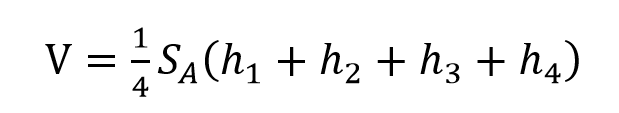
图3.14 基于正方形格网的体积量算
3.1.5 形态量算
3.1.5.1曲率和弯曲度
1.曲率
曲率反映线状要素的局部弯曲特征,其在数学上的定义为曲线切线方向角相对于弧长的转动率,可以用单位弧段上切线转过的角度的大小来表达弧段的平均弯曲程度。
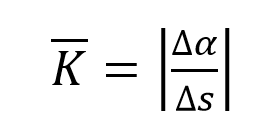
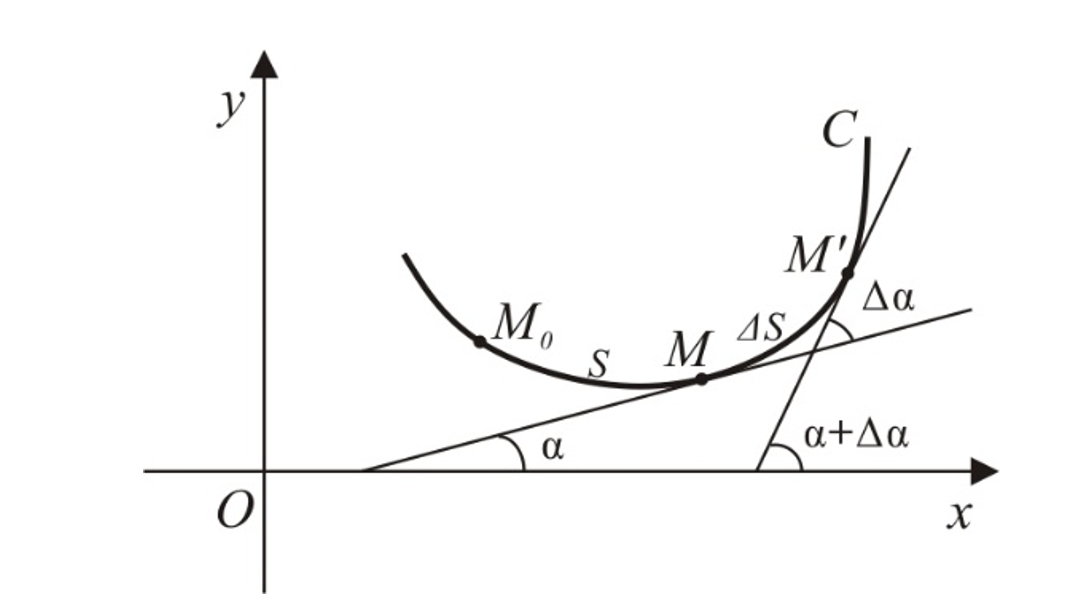
为了反映曲线的整体弯曲特征,需要计算的往往是曲线的平均曲率。一个简单的方法是将曲线进行n等分,先在各分线段上计算该段的平均曲率,然后汇总各段曲率并取其平均值作为整体曲率。
曲率的应用不仅限于描述曲线的弯曲程度,还具有工程和管理等方面的意义。例如,河流的弯曲程度会影响汛期河道的通畅情况;高速公路设计时也需要根据行车速度设计弯道的曲率;山区公路的曲率会影响汽车的行驶速度和乘客乘座的舒适性。此外,在地貌特征研究、径流分析、土地利用、生态景观、旅游线路规划等方面的研究中,往往也需要分析线状要素或多边形边界线的曲率。
2.弯曲度
弯曲度,也叫伸长度,为曲线长度与曲线两端点线段长度之比。伸长度系数q=L/l
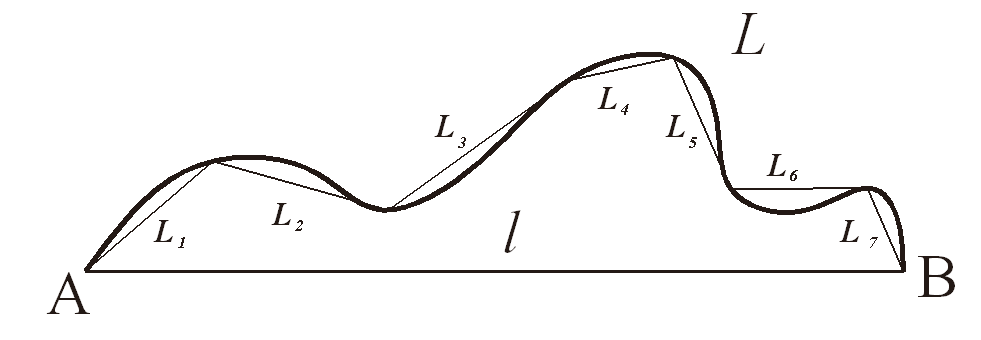
3.1.5.2形状系数
对于面状要素,通常采用形状系数r来描述其空间特征。
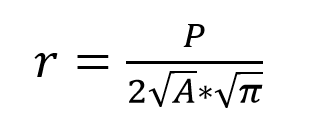
式中,P为面状要素的周长,A为面积。
r越小,表示目标物体越紧凑;
r=1时,目标物体为一个标准圆;
r越大,表示目标物体越膨胀。
3.1.6 ArcGIS中的几何量算工具
采用ArcGIS中的Calculate Geometry工具进行计算。前提是所加载的数据必须有投影信息。
3.1.6.1 点的几何量算:点的坐标(x,y)
3.1.6.2 线的几何量算:包括长度、线的起点坐标(x,y)、线的终点坐标(x,y)、线的中点坐标(x,y)。
3.1.6.3 多边形的几何量算:包括面积(Area)、周长(Perimeter)、质心点标(x,y)。