计算复杂度

来源：https://blog.csdn.net/yan_jin_feng/article/details/98172281

求极限

n->无穷大：

表达式n:–>无穷大

表达式1/n:—>0

(2n2+2n3+n)/n^3

2/n+2+1/n^2

n–》无穷大的时候：

2/n–》0

1/n^2-》0

2–》常数—》此算法的时间复杂度是n^3

时间复杂度的概念：

执行的次数和同数量级（n最高次方数）取商是常数

，那么同数量级就是这个算法的时间复杂度

时间复杂度的计算过程：

1 算出每一行语句执行的次数

2 求和，推导出一个n的表达式T(n)

3 找出同数量级的表示式（n的最高次方）

4 T(n)/同数量级–>常数，那么同数量级就是此算法的时间复杂度

举例1：

for i in range(n): #n

for j in range(5) : #5n

print(i,j)      #5n

print(100)              #1

T(n)=n+5n+5n+1=11n+1

第三步：同数量级：n

第四步：(11n+1)/n=11

时间复杂度：T(n)=O(n)

举例2：

常数阶

Temp=i;

i=j;

j=temp;

以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关

的常数。算法的时间复杂度为常数阶，时间复杂度记作T(n)=O(1)。

如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执

行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。

举例3：

n阶：

for i in range(n): #n

print(1)       #n

2n–>n

时间复杂度：O(n)

举例4：

n2阶：

for i in range(n): #n

for j in range(n): #n^2

print(1)       #n^2

T(n)=2n^2+n

时间复杂度：O(n)=n^2

举例5：

n^3阶：

for i in range(n): #n

for j in range(n): #n^2

for m in range(n): #n^3

print(1)       #n^3

T(n)=2n3+n2+n

时间复杂度：O(n)=n^3

举例5：

对数阶

i=1; ①

while (i<=n) #x表示它的执行次数

i=i2; ② 每执行一次，都会2,所以运行次数为2的f(n)次方

解：语句1的频度是1,

设语句2的频度是f(n), 则：2^f(n)<=n;f(n)<=log2n

取最大值f(n)= log2n,

时间复杂度：T(n)=O(log2n )

技巧：循环n的时候，循环体里面有了一些条件，让n的执行次数变小，那么就可以认

为是log2n的时间负责度

举例6：

n的对数阶：nlog2n

for i in range(n):

i=1;          ①执行1次

while (i<=n)  #x表示它的执行次数

i=i*2;

时间复杂度：T(n)=O(nlog2n )

时间复杂度常用的记忆法：

1）访问数组中的元素是常数时间操作，或说O(1)操作。

2）一个算法如 果能在每个步骤去掉一半数据元素，如二分检索，通常它就取O(logn)

时间。

3）用strcmp比较两个具有n个字符的串需要O(n)时间。

4）常规的矩阵乘算法是O(n^3)，因为算出每个元素都需要将n对 元素相乘并加到一起

，所有元素的个数是n^2。

5）指数时间算法通常来源于需要求出所有可能结果。例如，n个元 素的

6）集合共有2n个子集,所以要求出所有子集的算法将是O(2n)的。指数算

7）法一般说来是太复杂了，除非n的值非常小，因为，在 这个问题中增

8）加一个元素就导致运行时间加倍。

在计算时间复杂度时，我们一般使用的大O表示法，其时间复杂度，从小到大的排序是

：

(1) < (logn)< (n)< (nlogn)< (n^2)<…< (2^n)< (n!)

时间复杂度越大，时间越多，算的越慢

稳定排序

a=[1,2,-1,-2,3,5,3]

排序：用一个算法排序，排序之后，2个3（任意的多个相等值）的前后相对位置没有

发生变化。换句话说，在排序中，2个3没有进行过交换，那么就叫稳定排序。

————————————————

版权声明：本文为CSDN博主「yan_jin_feng」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/yan_jin_feng/java/article/details/98172281

以下来自：https://www.cnblogs.com/zxhyJack/p/10596735.html

复杂度分析

一、什么是复杂度分析

1. 
   

2. 数据结构和算法本身解决的是“快”和“省”的问题，衡量算法执行效率的指标就包括复杂度

3. 
   

4. 复杂度分析包括时间复杂度和空间复杂度分析，时间复杂度是指算法执行的时间与数据规模的关系，空间复杂度是指算法占用的空间与数据规模的关系

5. 
   

二、为什么需要时间复杂度分析

1. 
   

2. 通过测试、统计、监控，可以的得到算法执行的时间和占用的内存大小，但是测试结果非常依赖测试环境，测试结果受数据规模的影响很大

3. 
   

4. 我们需要一个不依赖测试环境和数据规模就可以粗略估算算法执行效率的方法

5. 
   

三、如何进行复杂度分析

1.大O复杂度表示法

• 
  

• 包括大O时间复杂度表示法和大O空间复杂度表示法

• 
  

• 大O时间复杂度表示法表示代码执行时间随数据规模增长的变化趋势，又称渐进时间复杂度

• 
  

3. 
   

4. 大O空间复杂度表示法表示代码执行所占的内存空间随数据规模增长的变化趋势，又称渐进空间复杂度

5. 
   

2.时间复杂度分析法则

1). 所有代码的执行时间T(n)与每行代码的执行次数成正比

  $T(n) = O(f(n))$

• 
  

• n表示数据规模的大小

• 
  

• f(n)表示每行代码执行的次数总和

• 
  

• 大O表示代码的执行时间T(n)与f(n)表达式成正比

• 
  

2). 只关注循环次数最多的一段代码

3). 加法法则：总的时间复杂度等于量级最大的那段代码的时间复杂度

$如果T1(n)=O(f(n)), T2(n)=o(g(n));那么T(n)=T1(n)+T2(n)=max(O(f(n)),O(g(n)))=O(max(f(n),g(n)))$

4). 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

$如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)T2(n)=O(f(n))O(g(n))=O(f(n)*g(n)).$

tips:复杂度分析关键在于“熟练”，无他，唯手熟尔

几种常见时间复杂度实例分析

分为两类：

• 
  

• 非多项式量级：$O(2^n)$和$O(n!)$ 低效的算法

• 
  

• 多项式量级 除非多项式量级剩下的全是多项式量级

• 
  

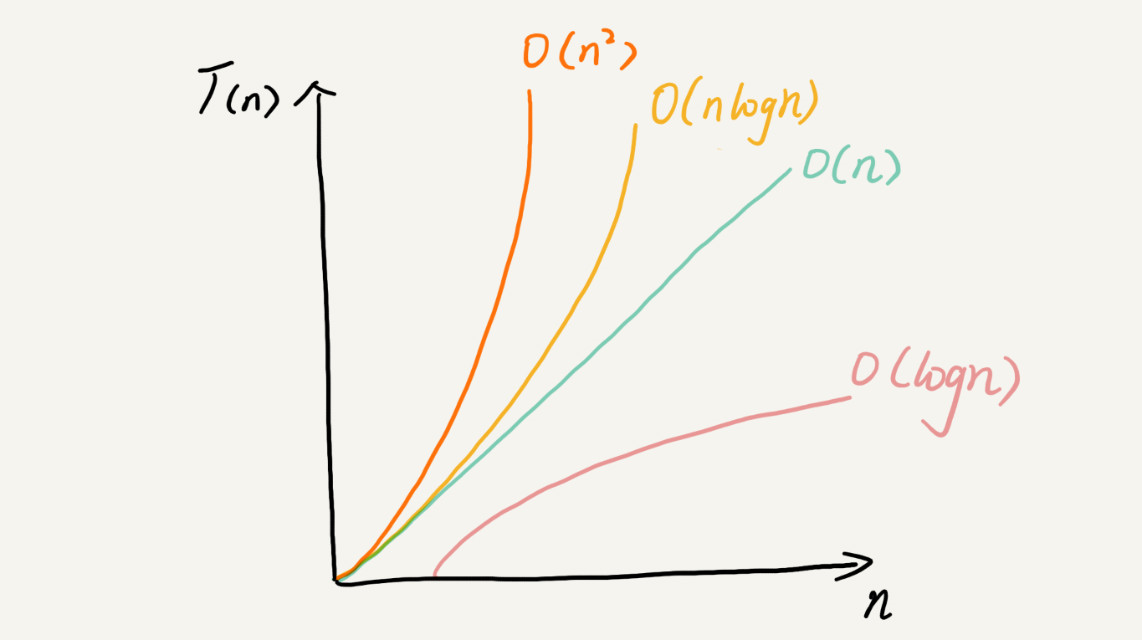
常见的复杂度有低阶到高阶有：$O(1),O(log(n)),O(n),O(nlogn),O(n^2)$

空间复杂度分析

空间复杂度全称渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系

四、最好、最坏、平均、均摊时间复杂度

1. 
   

2. 最好情况时间复杂度：在最理想的情况下，执行这段代码的时间复杂度

3. 
   

4. 最坏情况时间复杂度：在最糟糕的情况下，执行这段代码的时间复杂度

5. 
   

6. 加权(期望)平均时间复杂度：代码在所有情况下执行次数的加权平均值表示

7. 
   

8. 均摊时间复杂度：在代码执行的所有复杂度情况中绝大部分是低级别的复杂度，个别情况是高级别复杂度且发生具有时序关系时，可以将高级别复杂度用的时间均摊到低级别时间复杂度上，当低时间复杂度出现的概率远远大于高时间复杂度时，均摊的结果近似等于低时间复杂度。