1 递归调用概念
所谓递归即程序对自身的调用,是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型的复杂问题层层转化为一个与原问题相似但规模较小的问题来求解。
经典案例1
汉诺塔是一个可以使用递归解决的经典问题,它源于印度一个古老传说:大梵天创造世界的时候做了三根金刚石柱子,一根柱子上从下往上按照从大到小的顺序摞着64片黄金圆盘,大梵天命令婆罗门把圆盘从下面开始按照从大到小的顺序重新摆放在另一根柱子上,并规定,小圆盘上不能放大圆盘,三根柱子之间一次只能移动一个圆盘。问一共需要移动多少次,才能按照要求移完这些圆盘。
案例分析
假设一共有n个圆盘,移动的次数为f(n):
(1)当n=1时,只需将圆盘从A移动到C,移动结束。f(1)=1;
(2)当n=2时,将A柱顶层的圆盘移动到B柱,将底层的圆盘移动到C柱,再将B柱上的圆盘移动到C柱,移动结束。f(2)=3;
(3)当n=3时,将A柱自顶向下的第一个圆盘移动到C柱,第二个圆盘移动到B柱,将C柱上的圆盘移到B柱,将A柱的最后一个圆盘移动到C柱,将B柱上的第一个圆盘移动到A柱,将B柱的圆盘移动到C柱,再将A柱的圆盘移动到C柱,移动结束。此时f(3)=7;
……
依次类推,可以得出规律:f(n+1)=f(2n)+1。
根据公式可知,该问题符合递归的规律,因此该问题可使用递归方式求解。
经典案例2
兔子数列又称斐波那契数列、黄金分割数列,因数学家列昂那多·斐波那契以兔子繁殖为例而引出,故得此名,具体描述如下:一对兔子在出生两个月后,每个月能生出一对小兔子。现有一对刚出生的兔子,如果所有兔子都不死,那么一年后共有多少对兔子?
案例分析
案例要求编程解决此问题,并把最终结果输出到屏幕上。
对该问题进行分析,以n表示月份,可知第n个月时兔子的数量等于第n-1个月时兔子的数量,加上第n-2个月时兔子的数量,以f(n)表示每个月兔子的数量,则满足以下公式:
f(n)=f(n-1)+f(n-2) (n>1)
将f(n)视为一个关于月份的函数,根据上述公式可知,在求解当月兔子数量时,需要再次借用该函数自身。
2 递归调用形式
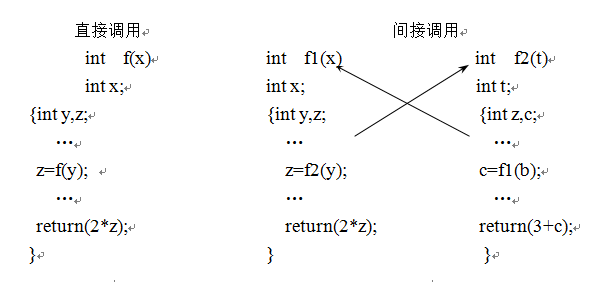
递归有两种形式,即:直接递归和间接递归。
直接递归是指在一个函数中包含对其本身的调用,而间接递归是指函数P在调用其他函数Q时,而函数Q又直接或间接地调用函数P。
程序中不应该出现无终止的递归调用,而只应出现有限次数的、有终止的递归调用。一般使用if语句进行控制,当某一条件成立时继续执行递归调用,否则终止递归调用。
递归问题求解一般需要满足以下三个条件:
原问题能够向另一个相对更简单的问题转化;
转化后的问题和原来问题求解类似;
转化能够有一个终止的条件。
【例8.7.1】计算Fibnbcci数列。
递归函数形式:
long fib(n)
int n;
{
long f;
if(n==0) f=0;
else if(n==1) f=1;
else f=fib(n-1)+fib(n-2); // 此处调用其本身函数,为直接递归
return f;
}
............................
上述程序不完整,同学可以自行补充主函数并完成调用


