什么是概率？

1 争论

概率论需要回答的第一个问题就是，什么是概率？

刚接触这门学科的同学可能觉得难以置信，这个问题仍然存在着广泛的争论：

而且这个问题更像是一个哲学问题，而不是数学问题，确实也有不少哲学家参与讨论。

对于概率的定义有几个主流的派别：

2 频率派

首先来了解下频率派，频率派的理论基础是对过去事实的归纳总结。

2.1 什么是频率？

学概率从抛硬币开始才是正确姿势。我们知道硬币是有正反两面：

硬币抛出之后：

得到的结果是随机的，那么得到正面的概率是多少呢？这里的“概率”又指的是什么？

我们扔100次硬币试试：

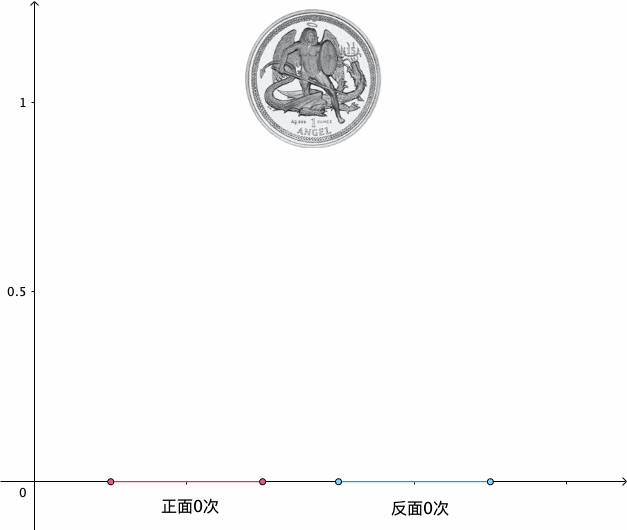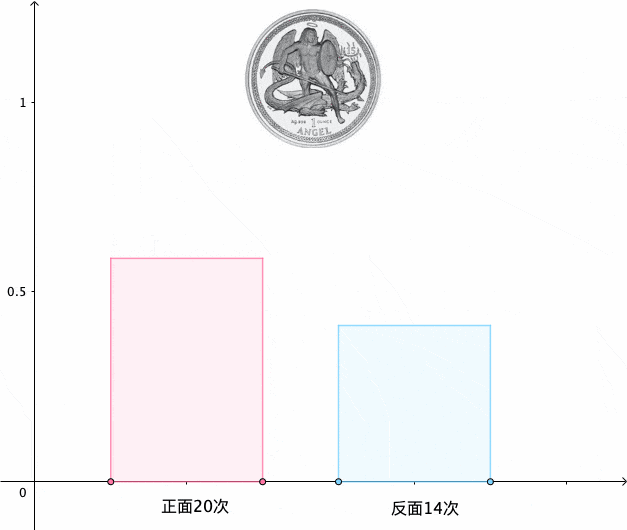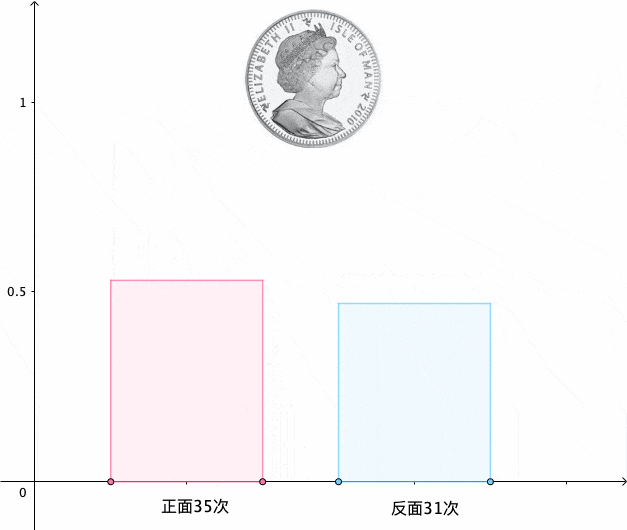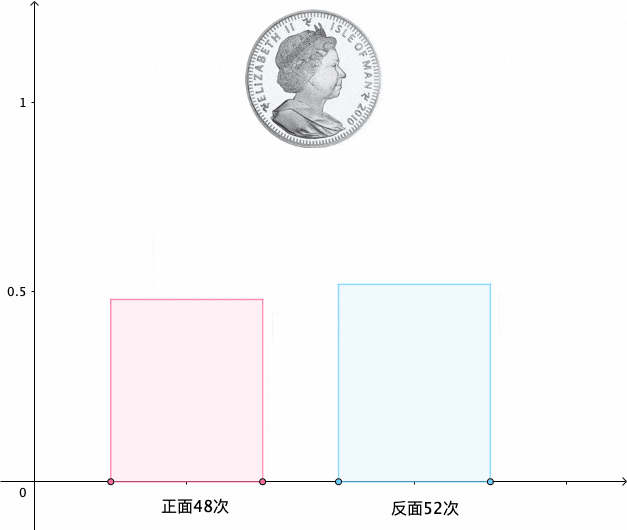
可以看到，得到48次正面，52次反面，用正面次数除以总的次数：

 ”称为扔100次硬币时，正面出现的 频率 。

2.2 频率与概率

2.2.1 频率稳定性

为此时正面出现的频率。历史上很多数学家都做过扔 次硬币的实验：

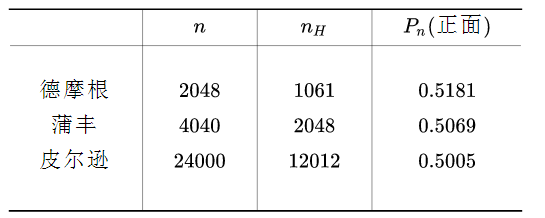
从试验结果可见，随着 的增大，频率越来越趋近于0.5。可见，虽然单次扔硬币的结果是随机的，但多次重复后频率趋于稳定，这种稳定性也称为 频率稳定性 ，反应了扔硬币存在某种必然性。

2.2.2 定义

频率派认为如果频率存在稳定性，即当 时下面极限存在，就得到了 概率 （用Probability的首字母P来表示）：

3 频率派的缺点

通过频率来定义概率的方法比较符合直觉，但缺陷也很明显：

首先，需要 足够大，但是“足够大”这个词很含糊

其次，需要在相同条件下反复扔硬币，但是“相同条件”这个词也很含糊，也很难保证，比如扔了10000次后，硬币上沾满汗水，那又怎么办？

再次，永远也不可能扔无限次硬币，所以得到的概率始终是一个近似值

最后，有些时候根本不具备反复实验的条件，比如火山喷发的概率应该怎么计算？

4 古典派

接下来介绍古典派，古典派的理论基础是不充分理由原则。

4.1 不充分理由原则

在概率论草创阶段，雅各布·伯努利（1654－1705）：

就提出，如果因为无知，使得我们没有办法判断哪一个结果会比另外一个结果更容易出现，那么应该给予它们相同的概率。比如：

硬币：由于不清楚硬币哪一面更容易出现，那么应该给予正面、反面相同的概率，即为1/2

骰子：我们不清楚骰子哪一面更容易出现，那么应该给予每一面相同的概率，即为1/2

此称为 不充分理由原则 （Insufficient Reason Principle）。

4.2 古典概率

以不充分理由原则为基础，经由拉普拉斯（皮埃尔-西蒙·拉普拉斯侯爵，1749－1827）：

之手，确立了 古典概率 的定义，即：

                                                     未知的概率都为等概率

在这之后，古典概率在整个19世纪也被人们广泛接受，我们高中学习的概率，基本都是古典概率。

5 古典派的缺点

古典派的缺陷也是非常明显的：

（1），古典派的概率定义，“未知的概率都是等概率”，有循环定义的嫌疑。

（2），不充分理由原则没办法处理非等概率的情况，假如被告知硬币两面是非等概率的，但是不知道是哪一面，那么应该怎么办？（拉普拉斯提出还是应该按照等概率来处理）

6 主观派

最后介绍下主观派，主观派认为概率是 信念强度（degree of belief）。

比如说，我个人相信20年后人类从网络时代进入人工智能时代的概率为70%：

上面说的概率也就是主观概率，是个人对这个命题的信念强度，换句话说我觉得还是很有可能实现的。

虽说是主观概率，其实也有客观的部分，比如刚才对人工智能的判断，就是基于AI的基础设置发展、计算速度的提高等事实。

主观概率更贴近人的思考方式，比如我们在作科学研究时，会先给出一个猜想，这就是给出了一个主观概率。

所以在人工智能时代，因为要模仿人的行为，主观概率越来越受到重视：

当然主观派缺陷也很明显，这也是被大家接受困难的原因：

• 说到科学，大家都认为应该是客观的，但是偏偏主观概率不客观，充满了个人偏见

  因为主观，大家很难对某个主观概率达成共识

  7 小结

• 三个流派大概有以下的区别：

• 

• 这三个流派并非泾渭分明、互不相容，反而在发展中犬牙交错。比如要判断火山的喷发概率，就需要总结过往数据（频率派），再加入主观知识（主观派）。

• 为什么概率的定义不明确？可能因为概率本身研究的就是“不明确”。

————————————————

版权声明：本文为CSDN博主「马同学高等数学」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/ccnt_2012/article/details/88416319