[例1] 

       一个电子处于宽度为a的一维无限深方势阱的基态,阱的两壁突然反向运动，使阱宽度变为 2a，试求电子留在基态的概率。

解：因阱壁突然反向运动，阱宽由a→2a,电子波函数来不及改变，它并不是2a 阱中的本征态但可由后者展开。

已知： 宽度为a时

宽度为2a时

将前者的基态波函数用后者本征函数用后者展开

所以

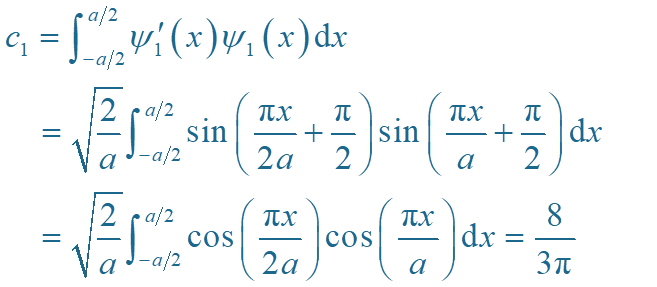
电子留在基态的概率

[例2] 

设 x=a 处有一维 d 势垒

          U(x)=A d(x－a), ( A  > 0)

能量为E的粒子从左方入射，求透射系数。

解：根据定态薛定谔方程

显然，波函数的二阶导数在 x = a 处发散，对方程在区间[a-e , a+ e ]积分，得

可见波函数一阶导数在 x = a 处不连续，但是这个问题的粒子几率连续，故波函数连续。波函数可写为

k 称为波矢。

将此波函数代入一阶导数在 x = a 处不连续条件, 有

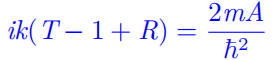
由 ψ 在 a 处连续

上两式联立，消去 R, 得

透射系数为