一、 势垒贯穿

势垒贯穿效应（隧道效应）纯粹是一种量子效应!

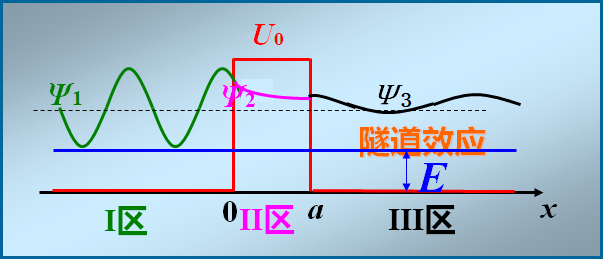
设粒子受到的作用势为

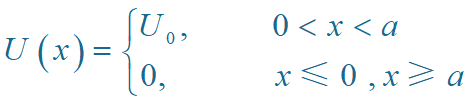
根据定态薛定谔方程：

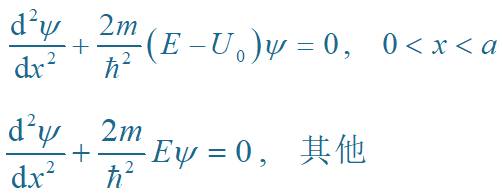
讨论：

（1）当  E > U0 时，令

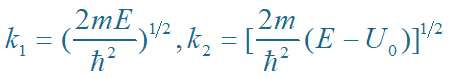
解得

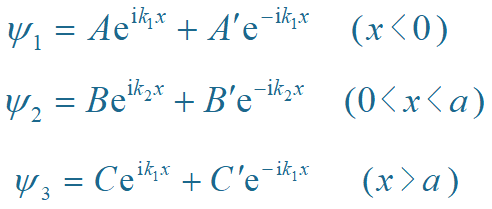
利用波函数连续条件, 得

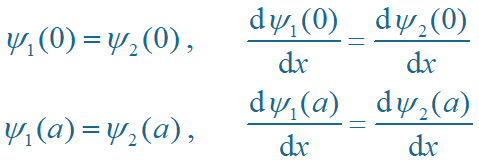
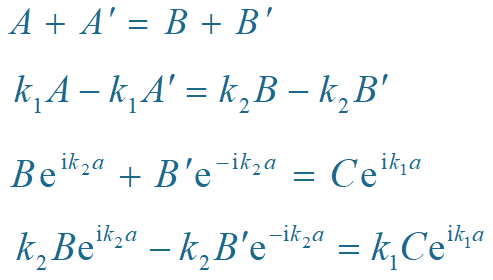
联立解得

入射波的概率流密度

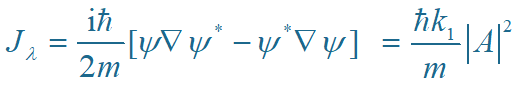
透射波的概率流密度

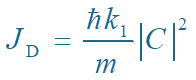
反射波的概率流密度

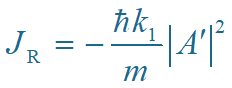
透射系数 D

D=透射波概率流密度∕入射波概率流密度

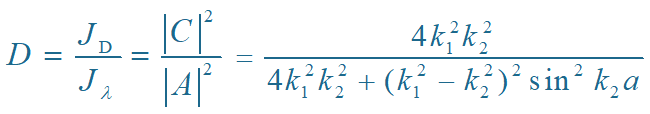
反射系数 R

R=反射波概率流密度∕入射波概率流密度

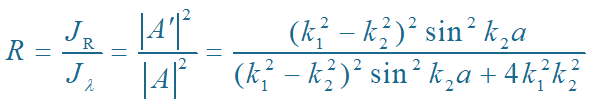
容易证明：

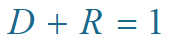
（2）当  E < U0 时，令

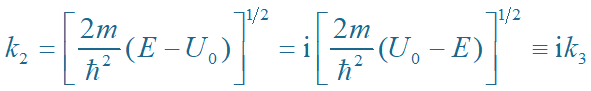
透射系数 D

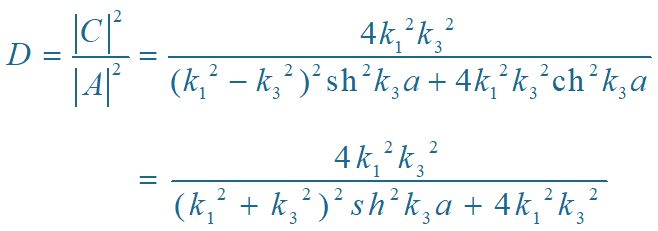
反射系数 R

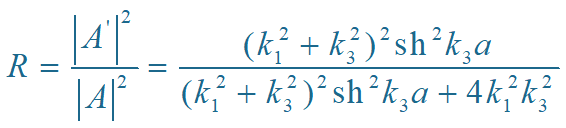
则有

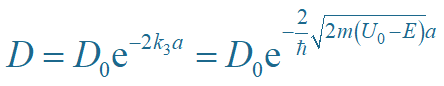
透射系数 D 随势垒的加高、加宽而减少。

       如果势垒的形状是任意的，整个势垒看做是许多方形势垒组成的。贯穿整个势垒的透射系数应等于贯穿所有这些方形势垒的透射系数之积。

设每个方形势垒宽为dx，高为U(x) ,则 

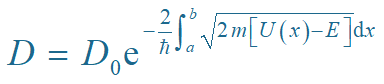
 讨论：

（1）全反射：D 随势垒宽度 a 和高度 U0增大而衰减.

若设 a→∞ 或 U0→∞, 则 D→0, 即无透射波，粒子在势垒边界全反射。

即：当 k3a→∞ 时，

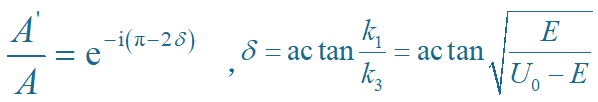
反射系数：

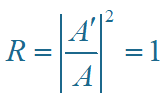
势垒为无限大时，d®0。反射波与入射波位相差为π（反射波落后入射波）即存在所谓 半波损失。

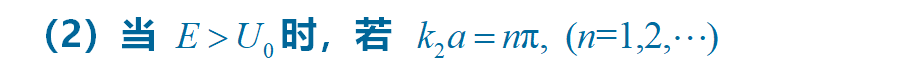
即：粒子能量为

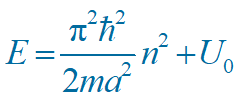
则 D = 1， R = 0.

即粒子全部通过势场，称为 共振散射。

二、应用

1）α衰变，金属冷电子发射

2）扫描隧穿显微镜（STM）

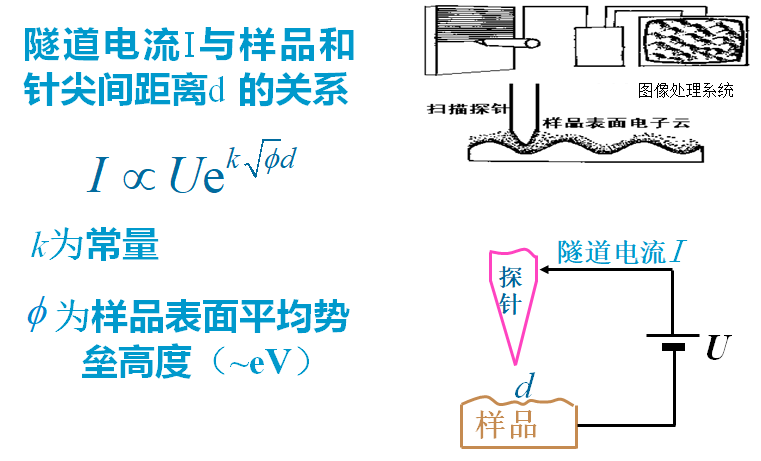
STM用于观察表面的微观结构（不接触、不破坏样品）