薛定谔方程的简单应用

二、 线性谐振子

粒子势能为

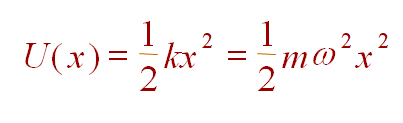
其中: k 或 w 是常数的体系称为线性谐振子。根据定态薛定谔方程：

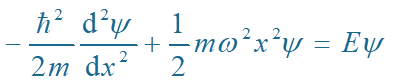
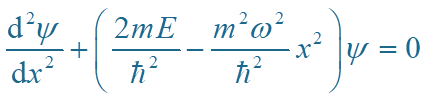
令

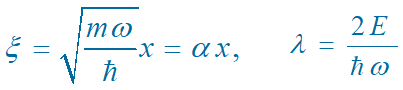
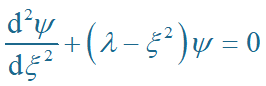
考察 x®±¥ 的渐近形式。设

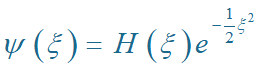
且当x®±¥ 时，H(x) 有限，得

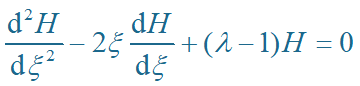
利用级数解法，为使当x®±¥ 时y 有限，l 应取奇数

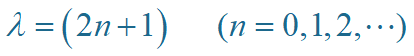
故：线性谐振子的能级

能量本征波函数

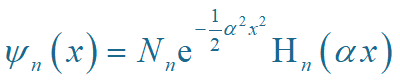
由归一化条件：

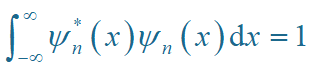
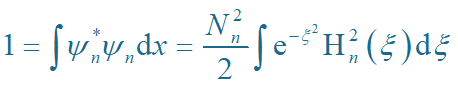
利用厄米多项式的正交条件

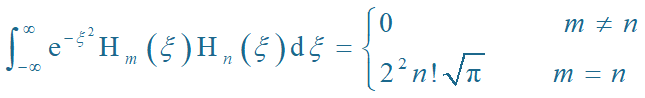
得归一化常数

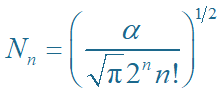
讨论：

（1）能量量子化

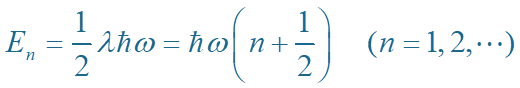
基态：

（2）n 的奇偶性决定了谐振子波函数的奇偶性

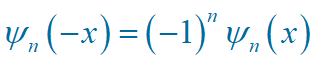
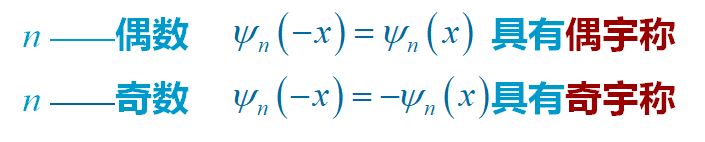
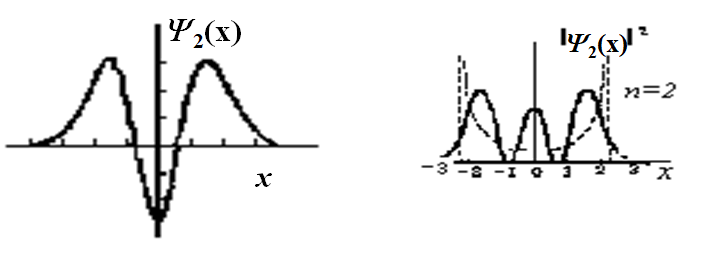
（3）本征函数和概率密度分布

（4）常用递推公式