薛定谔方程的简单应用

一、 一维无限深方势阱

根据定态薛定谔方程：

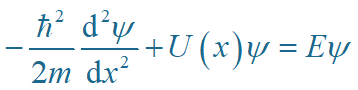
阱外

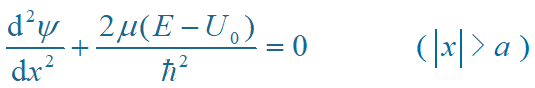
因U0  → ∞，根据波函数的连续性和有限性条件，得

阱内

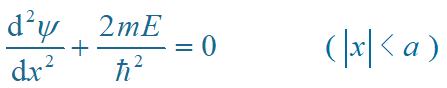
解得

由波函数连续性条件

由此得到

A 与 B 不能同时为零，因此得两组解

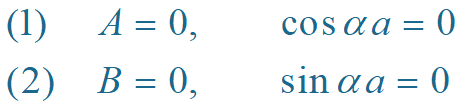
由此可得

对于第一组解, n 为奇数

对于第二组解, n 为偶数

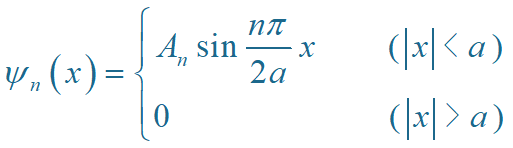
两组解可合并为

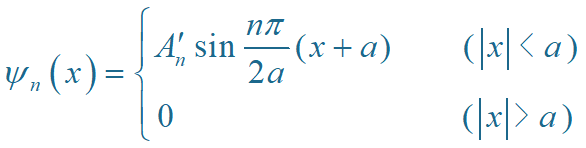
归一化：

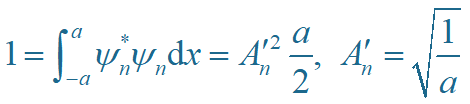
所以, 波函数

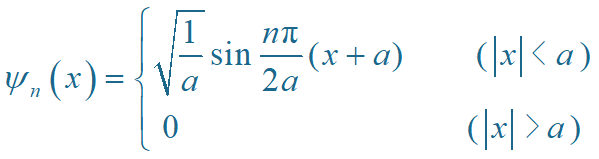
体系的能量

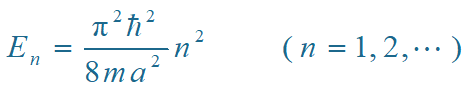
注：

• ① E 正比于 n 平方,能级越高, 能级间隔越大。

当n→∞时

       ，    

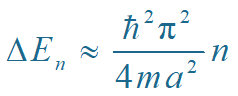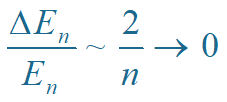
能量可认为是连续的！

• ②基态: n=1，能量最低状态. 

基态波函数无结点。

第 k 个激发态（n=k+1）,有 k 个结点, 

节点的存在是量子效应.

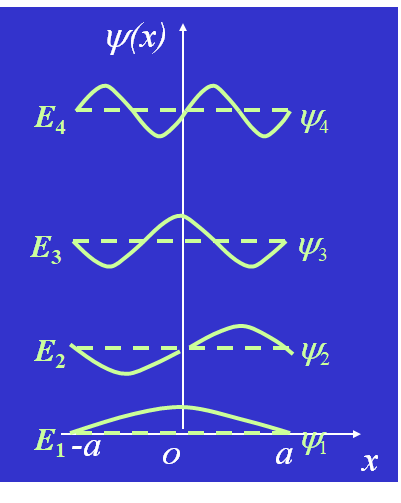
• ③束缚态: 

   无限远处为零的波函数描写的状态。