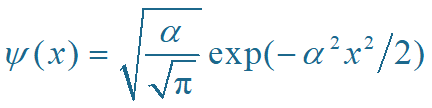1.波函数

量子力学基本假说之一 ：

       一切微观粒子的状态可用相应的波函数来描写.

自由粒子：

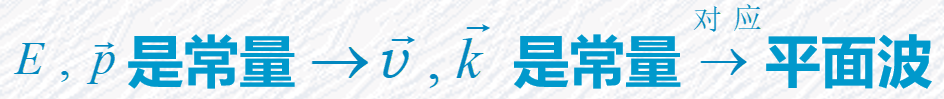
自由粒子平面波函数:

用一个函数描写粒子的波,称这个函数为波函数。

2. 概率波

德布罗意：

“物质波”不是经典波所代表的某种物理量的波动，而是所描写粒子空间分布的概率波，把粒子的“原子性”与波的“叠加性”统一了起来。

电子衍射实验：

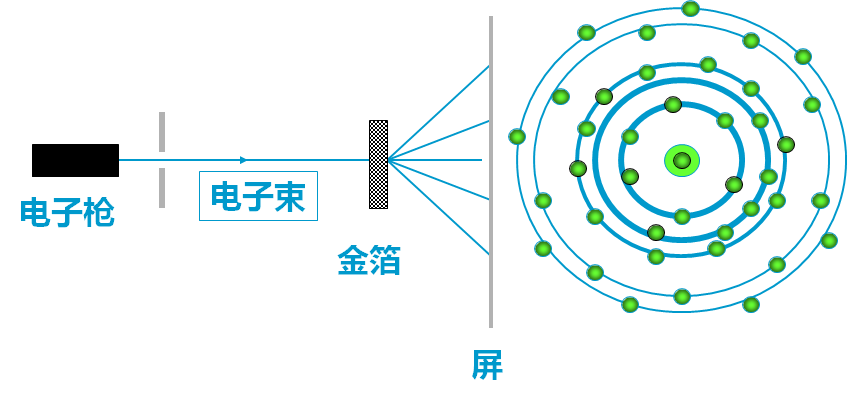
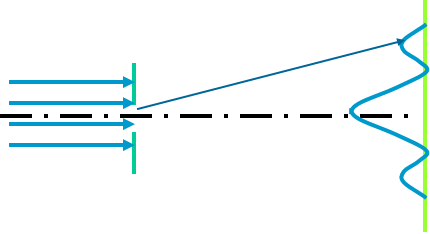
因为 x 处的强度∝x 处感光点子数

                        ∝ x 处电子数

                        ∝电子出现 x 处的几率

      又因为强度 ∝ 波幅平方

所以，电子在t 时刻，x 处的概率 ∝ 电子波函数的模方

玻恩（M.Born)：

       在某一时刻, 空间 x 处粒子出现的概率正比于该处波函数的模方。粒子在空间出现的概率具有波动性的分布，它是一种概率波。

设波函数为Ψ (x,y,z,t )，则 t 时刻处于 x—x+dx，y—y+dy，z—z+dz内的概率

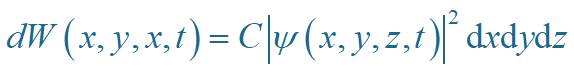
概率密度：

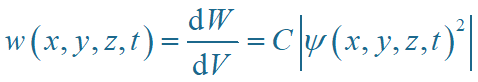
3.波函数的性质

(1)Ψ (x,y,z,t ) 是单值、有界、连续的；

(2)Ψ (x,y,z,t ) 与 CΨ (x,y,z,t ) 描写同         一状态。

(3)波函数的归一性

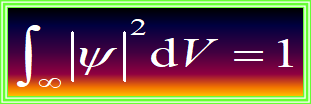
如：平面波函数

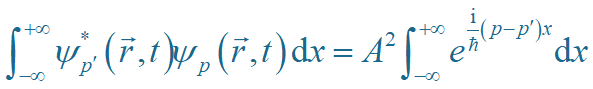
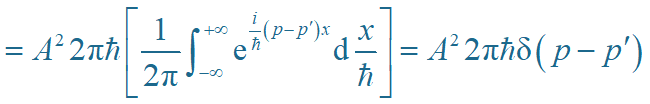
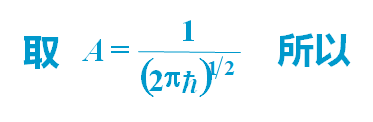
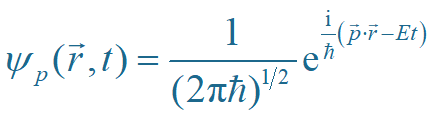
③ 箱归一化：加上周期性边界条件限制

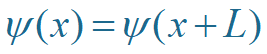
 L ——为 周期

存在不确定的相因子 （其既不影响空间各点粒子的概率，也不影响到归一性）

解：设归一化因子为C，则归一化的波函数为

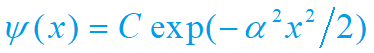
由 

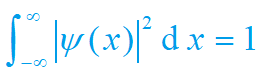
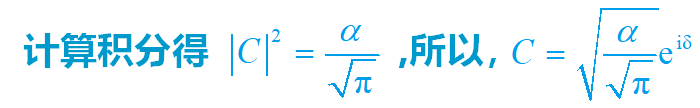
取 d＝0，则归一化的波函数为