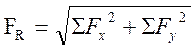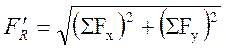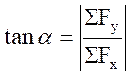四杆机构的设计

四杆机构的设计

四杆机构设计的任务，主要是根据给定条件选择四杆机构的形式，并确定机构的尺寸参数。

四杆机构的设计方法有解析法、图解法和实验法三种。解析法精确度较高，虽计算繁复，但随着计算机的普及和应用，计算机辅助设计四杆机构已成为必然趋势。实验法烦琐、费时且不精确。本节只要介绍比较直观、简明，易于操作的图解法。在计算机辅助设计中，由各参数的函数式，用Matlab软件计算出机构的轨迹点的坐标，拟合出机构的轨迹，从而画出相应的四杆机构.

1.       按给定的行程速比系数设计四杆机构

给定的行程速比系数K，就是给定了四杆机构急回运动的条件，从而确定了极位夹角；根据其它一些限制条件及极位夹角，可用作图法方便地作出该四杆机构。

      设已知摇杆长度L_CD、摆角Ψ和行程速比系数K。试设计该曲柄摇杆机构。

设计分析：如图2-65a所示，显然在已知摇杆长度L_CD、摆角Ψ的情况下，只要能确定A铰链的位置，则在量得L_AC1和L_AC2后，可求得曲柄长度L_AB和连杆长度L_BC

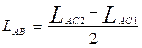
L_AD可直接量得。如图2-65b所示由于A点是极位夹角的顶点，即∠C₁AC₂=θ，如过AC₁C₂三点作辅助圆，由几何知识可知，在该圆上任取一点A为顶点，其圆周角也是θ，且过辅助圆心O的圆心角∠C₁OC₂= 2θ。显然，当求得极位夹角θ后，用作图法容易作出辅助圆并得到圆心O，则问题迎刃而解。 

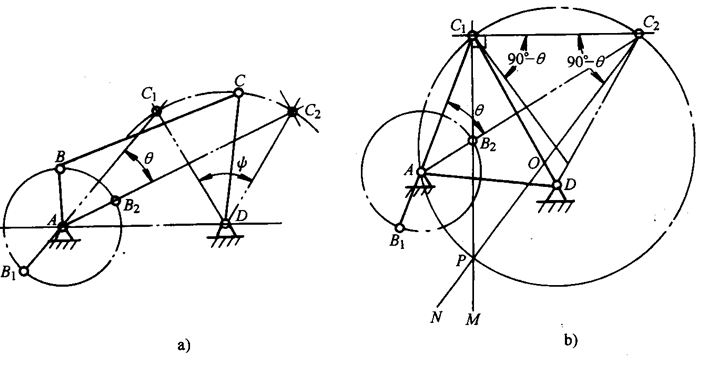
图2-65   按行程速比系数K设计

a）设计分析图  b）作图法

设计步骤：

    1）计算：按式（2-2）求得θ

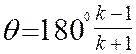
    2）作摇杆的两极限位置：任选摇杆回转中心D的位置，按一定的比例尺μ_l，根据已知的L_CD及摆角Ψ作出摇杆的两个极限位置C₁D和C₂D（图2-65b）。

    3）作辅助圆：联接C₁、C₂，并作与C₁C₂成90°-θ的两直线，设交于O点，则∠C₁OC₂ = 2θ。以O点为圆心，以OC₁（或OC₂）为半径作辅助圆。

    4）在上任取一点A为铰链中心，并连接AC₁和AC₂，量得L_AC1和L_AC2的长度，据此可求出曲柄和连杆的长度

    5）求其它杆的长度：机架L_AD可直接量得，乘比例尺μ_l既为实际尺寸。

注意，由于A点是在辅助圆上任选的一点，所以实际可有无穷解。若能给定其它条件，如曲柄长度L_AB、机架长L_AD或最小传动角γ_min等，则可有唯一的解。实际设计时，多数均有相应的辅助条件。

与上述方法相似，可在已知滑块行程s、偏距e和行程速比系数K的情况下，设计偏置曲柄滑块机构，或在已知机架长度和行程速比系数K的情况下，设计摆动导杆机构，具体设计步骤读者可自行导出。

2. 按给定的连杆位置设计四杆机构

设已知：连杆BC的长度l_BC及其两个位置B₁C₁、B₂C₂。

设计分析：图2-66可知，如能确定固定铰链A、D的中心位置，便可确定各构件的长度。由于连杆上B、C两点的轨迹分别在以A、D为圆心的圆周上，所以A、D两点必然分别位于B₁B₂、C₁C₂和中垂线b₁₂和c₁₂上。据此，可得设计方法和步骤如下：

    设计步骤：

    1）选比例尺μ_l，根据已知条件画出连杆的两个位置B₁C₁、B₂C₂。

    2）分别连接B_1、B₂和C_1、C₂点，并作它们的中垂线b₁₂和c₁₂。

    3）在b₁₂上任取一点A，在c₁₂上任取一点D，连接AB₁C₁D，则AB₁C₁D即为所求的四杆机构。各杆长度分别为：L_AB =μ_lL_AB1，L_CD=μ_l L_CD1，L_AD=μ_l L_AD。

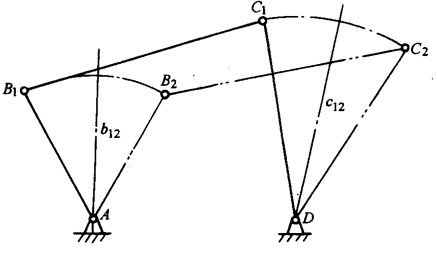
注意，在已知构件两个位置的情况下，由于A、D两点在是任取的，故有无数解。若给出其它辅助条件，如机架长度及其位置等，就可得出唯一解。此外，如给定连杆长度及其三个位置，则答案就是唯一的，读者可自行推出。

平面力系的简化

   在构件受力分析过程中，为了便于了解各力间的相互关系和作用效应，往往需要对作用于物体上的力进行移动、简化、合成、分解和投影。

   （1）力的合成与分解

根据力的平行四边形法则可将两个汇交力合成为一个合力，反过来，作用在物体上的一个力也可以分解为两个或两个以上的分力。两个汇交力合成的结果是唯一的，而力的分解可以有无数结果。如图2-67所示，以合力F_R为对角线可作出多个平行四边形，因此须事先确定分解合力的作用线方位。

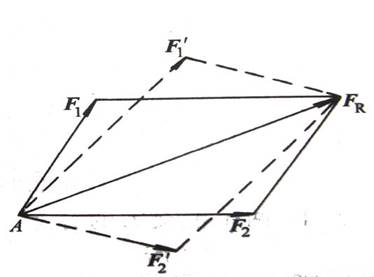
图2-67   力的合成与分解

   通常将一个力分解为沿两个互相垂直的坐标轴的正交分力F_x、F_y。如图2-68所示，过力F的未端作ｘ、ｙ轴的垂线，交ｘ、ｙ轴于A、B两点，则力矢OA、OB 即为分力F_x、F_y。

图2-68  力沿x、y轴分解

   （2）力在坐标轴上的投影

   如图2-69所示，在直角坐标系Oxy平面内有一已知力F，此力与x轴所夹的锐角为α。从力F的两端A和B分别向x、y轴作垂线，得线段ab和a′b′。其中ab称为力F在x轴上的投影，以F_x 表示；a′b′称为力F在y轴上的投影，以F_y 表示。

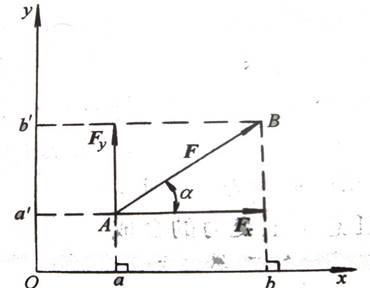
图2-69  力在坐标轴上投影

  力在坐标轴上的投影是代数量，有正、负号的区别，当投影的指向与坐标轴的正向一致时，规定为正号，反之为负号。

Ｆ_x =±Ｆcosα

                                  Ｆ_y =±Ｆsinα                    （2-5）

  （3）合力投影定理

合力在某一直角坐标轴上的投影，等于各分力在同轴上投影的代数和。

  据此定理可知，由n个力组成的力系，各分力和合力之间有如下关系：

                      F_Rx=F_x1+F_x2+…+F_xn=∑Ｆ_x

                 F_Ry=F_y1+F_y2+…+F_yn=∑Ｆ_y                           （2-6）

 即合力F_R 在x、y轴上投影等于力系中各分力在同轴上投影的代数和。

即，合力的大小和方向为：

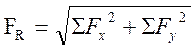                                                      (2-7)

                                                             (2-8)

求出合力与ｘ轴夹角α或，从而确定合力F_R的方向。

  若该力系作用于物体上，使物体处于平衡状态，则其合力等于零，即F_R=0。由式(2-7)可知：

                       ∑Ｆ_x= F_x1+F_x2+…+F_xn=0

                        ∑Ｆ_y= F_y1+F_y2+…+F_yn=0                           （2-9）

 （4）力的平移定理

  将作用于物体上某点的力矢平移到物体上的任一点后，将产生一附加力偶，其力偶矩等于该力对新作用点之矩。

  根据力的可传性原理可知，作用于刚体上的力可沿其作用线移至任何一点而不改变它对刚体的效应。但力的平移使力离开了原作用线，效果将会发生变化。力的平移定理就是关于这一问题的解答，同时也是平面任意力系简化的理论依据。

如图2-70所示，设作用于物体上Ａ点的力Ｆ，为将其平移至物体上B 点，可根据加减平衡力系原理，在点Ａ加上一对平衡力Ｆ′和Ｆ″，且令：Ｆ′= －Ｆ″=Ｆ，Ｆ′∥Ｆ。此时，由于Ｆ″与Ｆ是等值、反向，作用线平行，构成一对力偶，其矩为Ｍ（Ｆ，Ｆ″）=Ｆd =Ｍ_B（Ｆ）。即将力Ｆ 移至B点，同时产生了一对附加力偶。

图2-70 力的平移定理

由此可知，平移前的一个力与平移后的一个力及一个力偶等效。

力的平移定理揭示了力可以转换为同平面内的一个力和力偶。反之，同平面的一个力和力偶也可以合成为一个力。这不但是力系简化的理论基础，同时对分析和解决工程力学及日常生活中一些实际的力学问题也具有指导意义。例如，如图2-71所示，一对齿轮啮合传动，作用在轮齿上的力Ｆ_t可以使齿轮转动，这是因为作用于轮齿上的力不通过齿轮的回转中心，将力向齿轮中心平移，会得到一个作用于轴心的力及一个附加力偶Ｍ ，Ｍ使齿轮转动。

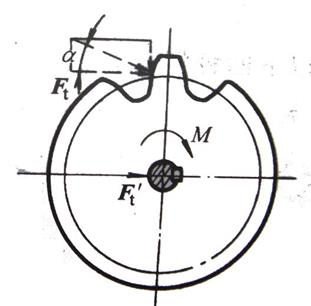
图2-71  齿轮的受力

（5）力偶及力偶系的合成

1）力偶的基本性质：

性质1：只要保持力偶矩大小和力偶的转向不变，作用于刚体上的力偶可以在其作用面内任意移动或转动，或同时改变力和力偶臂的大小而它对刚体的效应不变。

如图2-72所示的方向盘，只要保持力偶矩大小不变，加在A、B两点的力偶（F，F′）可以移到C、D点或E、F点。

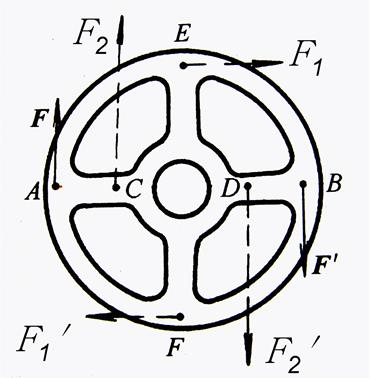
图2-72　方向盘受力

性质2：力偶在同一刚体上可以搬移到与其作用面相平行的平面内，而不改变其对刚体的效应。例如，图2-73所示轴上力偶 M作用于 A和 B的效果是一样。

图2-73  轴的受力

2）平面力偶系的合成  两个或两个以上力偶组成的力系称为力偶系。力偶系合成的结果只能是力偶而不是力，这个力偶称为合力偶。

根据力偶的等效变换可将平面力偶系合成为一个合力偶，合力偶矩等于各分力偶矩的代数和：

                        Ｍ==Ｍ₁+Ｍ₂+Ｍ₃=∑Ｍ_i                               (2-10)

（6）平面任意力系的简化

平面任意力系简化的方法是：应用力的平移定理，将平面任意力系的各力平移到作用面内任意点Ｏ（称为简化中心）。从而将平面任意力系转化为一个平面汇交力系和一个附加力偶系，把一般力系问题转化为简单力系问题来解决。

设刚体上作用有一平面力系Ｆ₁ ，Ｆ₂ ，… ，Ｆ_n，各力作用点分别为Ａ₁，Ａ₂，…Ａ_n，如图2-74所示，在刚体上力系所在平面内取点Ｏ作为简化中心，将各力向Ｏ点平移，得到两个基本力系：

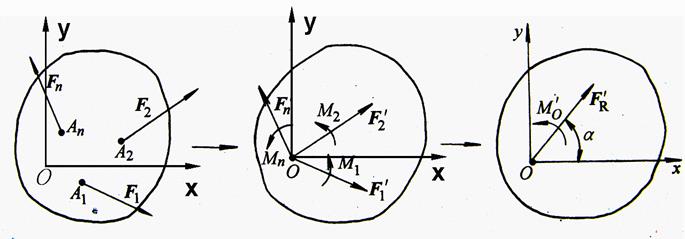
                          图2-74  平面任意力系的简化

    ① 汇交于Ｏ点的平面汇交力系：Ｆ₁′，Ｆ₂′，…，Ｆ_n′。

    ② 附加力偶系：Ｍ₁=Ｍo（Ｆ₁），Ｍ₂=Ｍo（F₂），…，Ｍ_n=Ｍo（Ｆ_n）；

其中，平面汇交力系可以合成为一个合力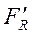作用于Ｏ点，称为主矢

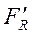= Ｆ₁′+Ｆ₂′+ … +Ｆ_n′= Ｆ₁+Ｆ₂+…+Ｆ_n=∑Ｆ

如以Ｏ点为原点建立直角坐标系，则主矢在ｘ、ｙ轴上投影为

∑Ｆ_x=Ｆ_x1+Ｆ_x2+…+Ｆxn

∑Ｆ_y =Ｆ_y1+Ｆ_y2+…+Ｆyn

利用式（2-4）、式（2-5）、式（2-6）可以进一步求出主矢的大小与方向

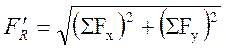
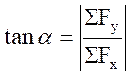                                                    (2-11)

式中,为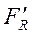与ｘ轴夹角。

附加力偶系也可以合成为同平面内的一个合力偶Ｍo′，称为主矩

      Ｍo′= Ｍo（F₁）+Ｍo（F₂）+ … +Ｍo（Ｆ_n）=∑Ｍo（Ｆ）    （2-12）

    由式（2-11）、式（2-12）可见，主矢取决于原力系中各力大小和方向，与简化中心Ｏ的位置无关；主矩的大小及转向取决于简化中心Ｏ的位置。

    综上所述, 平面任意力系向其作用面内一点简化，可得到一个作用线通过简化中心的力，即主矢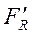，以及一个附加力偶，即主矩Ｍo′。主矢等于原力系中各力的矢量和，大小与简化中心Ｏ的位置无关；主矩等于原力系中各力对简化中心之矩的代数和，与简化中心Ｏ的位置有关。

应注意，主矢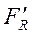不是原力系的合力，也就不能代替原力系对物体的作用。

平面力系的平衡问题

1.平面任意力系的平衡

根据前面的分析，平面任意力系向一点简化后，得到一个合力Ｆ_R′和一个合力偶Ｍo′。力和力偶不能互相平衡，因此要使力系平衡，应使主矢和主矩分别平衡。当主矢Ｆ_R′=0 时，力系对物体无移动效应；当主矩Ｍo′= 0 时，力系对物体无转动效应。因此，当主矢、主矩同时为零时，则力系平衡。即平面力系平衡的必要与充分条件是：力系简化所得主矢Ｆ_R′和主矩Ｍo′都等于零。也就是

  = 0

    Ｍo′=∑Ｍo（Ｆ）= 0

由此得到平面任意力系的平衡方程为

                                   ∑Ｆ_x = 0

                                   ∑Ｆ_y = 0                                               （2-13）      

                                   ∑Ｍo（Ｆ）= 0                  

   平面任意力系平衡的解析条件是：力系中各力在两个任选的直角坐标轴上的投影的代数和分别为零，以及各力对任一点之矩的代数和为零。

    式（2-13）中，前两个为投影方程，最后一个为力矩方程。平面任意力系的平衡方程还可以有以下不同的形式：

①  两矩式平衡方程     

         ∑Ｆ_x= 0

                          ∑Ｍ_A（Ｆ）= 0                     （2-14）

                                                               ∑M_B（F）= 0    （A，B连线不能垂直x轴）    

②  三矩平衡方程        

∑Ｍ_A=0

                          ∑Ｍ_B=0                         （2-15）

                                                      ∑Ｍ_C=0   （A、B、C三点不能共线）       

可以证明：当平面任意力系满足两矩式、三矩式平衡方程时，有Ｆ_R′= 0，Ｍo′= 0。

    不论何种形式的平面力系平衡方程,均只有三个独立方程，可求解三个未知量。在实际应用中选用那一种形式，主要取决于解题的方便。

2.  几种特殊平面力系的平衡方程

    平面任意力系的平衡方程是各种力系的一般形式，其它特殊平面力系平衡方程可根据一般形式推导出来。

   1）平面汇交力系的平衡方程

   根据前面分析可知，平面汇交力系可以合成为一个合力Ｆ_R，不可能有力偶。因此，一般方程中的∑Ｍo≡0，平衡方程只有两个，即

∑Ｆ _x = 0

         ∑Ｆ_y= 0                    （2-16）

    可见，平面汇交力系平衡的解析条件是：力系中各分力在直角坐标轴上投影的代数和分别为零。

   2）平面力偶系的平衡方程

   根据前面的分析知道，平面力偶系合成的结果是一个合力偶，则一般方程中∑Ｆx ≡0，∑Ｆy≡0。因而，平衡方程只有一个，即

                        ∑Ｍo（Ｆ）= 0                          （2-17）

因此，平面力偶系平衡的必要与充分条件是：力偶系中各分力偶矩的代数和为零。

3）平面平行力系

由于平面平行力系中各力均平行,所以建立直角坐标系时，可选择某坐标轴与各力平行，则另一坐标轴与各力垂直。如图2-75中令 y轴平行于各力，则各力在 x轴上的投影均为零。因而有∑Ｆ_x≡0，且∑Ｆ_y =∑Ｆ，因此一般方程中只余下两个：

                                                                    ∑Ｆ= 0

                                     ∑Ｍo（F）= 0                   （2-18）

即为平面平行力系的平衡方程。

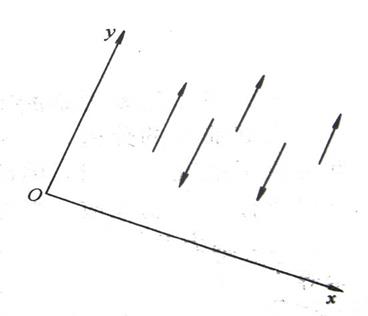
图2-75  平面平行力系

3. 平面力系平衡方程的应用

   应用平面力系的平衡方程来解决工程上的平衡问题，是静力学的主要任务之一。对于平面力系来说，一般形式的平衡方程是三个，最多可以求解三个未知量。如果是平面力系的特殊形式，则平衡方程数以及可求解的未知量数目相应减少。未知量可以是力的大小或方位，但一般不把力的指向作为未知量。在力的指向不能判明时，可先任意假定，再根据平衡方程计算结果来判断：如果计算结果为正，则假定的力的指向与实际相符；如果计算结果为负，则说明假定的指向与实际相反。

    例2-9  重为G =2kN 的球搁在光滑斜面上，用绳拉住， 如图2-76a 所示，已知α=30°, β=15°，求绳子的拉力和斜面对球的约束反力。

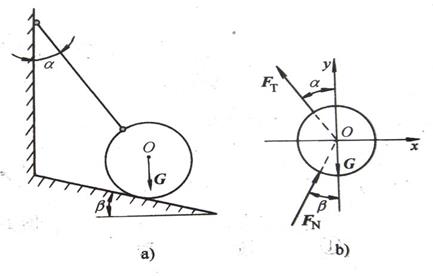
图2-76 求球的约束反力

   解：① 根据题目要求, 所要求的绳子拉力、斜面对球的约束反力均作用于球上, 故选取球为研究对象, 并画出分离体。

    ② 对球进行受力分析, 画出受力图如图2-74b所示。球受三个力作用, 其中重力方向垂直向下(已知)， 绳子拉力Ｆ_T沿绳子背离球体，斜面的约束反力沿过接触点的接触面公法线指向球体，这三个力的延长线均通过球心，因此球受平面汇交力系的作用。

    ③ 以球的中心为原点建立直角坐标系，根据平面汇交力系的平衡条件，列出平衡方程并求解如下

∑Ｆ_x=0     Ｆ_N sinβ－Ｆ_T sinα= 0

∑Ｆ_y=0     Ｆ_N cosβ+Ｆ_T cosα－G = 0

代入α=30°、β=15°，并解联合方程得：

Ｆ_N  =1.414N

Ｆ_T = 0.732N

方向如图2-74所示。

4. 物系的平衡问题分析与实例

   物系是指几个物体（如结构构件，机械零部件等）通过一定的约束联系在一起的物体系统。研究物系的平衡时，既要考虑整个系统的平衡，还要研究系统内单个物体的平衡。因此，必须选择合适的研究对象。在分析物系的平衡问题时，采取的基本原则和方法与前面介绍的单个刚体的平衡问题相一致。

系统以外的物体作用在系统上的力称为物系的外力，系统内各物体之间相互的作用力称物系的内力。所谓外力与内力，是视所取的研究对象而定的。

   如图2-77所示，一货车拉一拖车，当以单独的货车或拖车为研究对象时，Ｆ、Ｆ′为外力，而以整个拖车系统为研究对象时，Ｆ、Ｆ′则为内力。

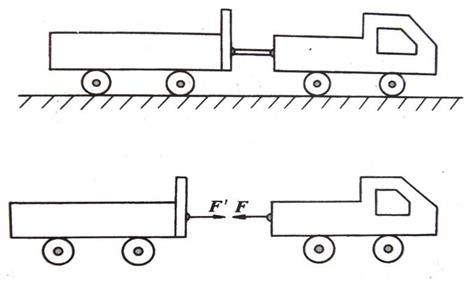
   图2-77  货车与拖车

    当以整个系统为研究对象时，物系的内力总是成对出现，作用于系统的两个相连的物体上的力是作用力与反作用力关系，在任意轴上的投影和对任意点的矩均为零，故不必考虑。但以单一物体为研究对象时，则应考虑。

    由于物系是由多个物体组成，因此研究对象的选择对于能否求解以及求解的简繁有着密切关系。可以单独或分别选取整个系统、局部系统或单个物体为研究对象，列出平衡方程求解。选取研究对象的原则是：

1）选取与已知量有关的物体；

2）研究对象中要反映出未知量；

3）所列平衡方程中包含的未知量数目最少。  

    例2-10  如图2-78所示，汽车发动机中曲柄滑块机构在图示位置时处于平衡。若工作阻力Ｆ_Q=0.4kN，不计各构件自重，试求作用于曲柄上的力偶矩M 和支座 O处约束力。

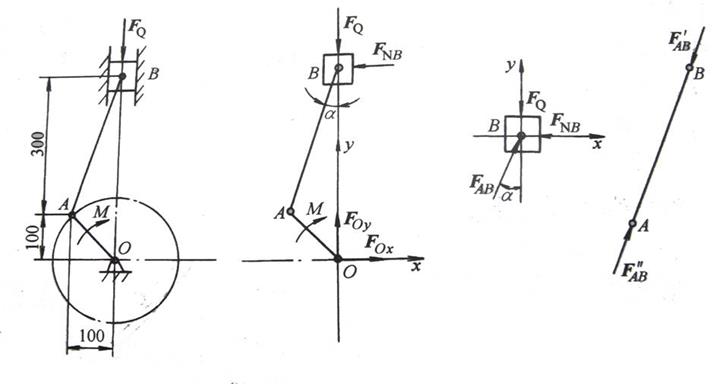
图 2-78   曲柄滑块机构受力分析

     解  ① 取滑块 B 为研究对象，画其受力图。其中F_Q为主动力，F_BN为汽缸壁的约束反力。由于AB为二力构件，可知F_AB′、F_AB″沿AB方向。又滑块上所受AB杆的作用力F_AB与F_AB′等值、反向，则可判断F_AB的受力。滑块上各力组成平面汇交力系，根据平衡条件列出平衡方程如下

∑F_y=0          Ｆ_AB cosα－Ｆ_Q = 0                         （1）

∑F_x=0          Ｆ_ABsinα－Ｆ_NB  = 0                        （2）

解得：                ，Ｆ_NB =Ｆ_Q tanα

其中：                       tanα=1/3，则Ｆ_NB  = 0.133kN

    ② 以整个物系为研究对象，画其受力图如图2-76所示。其中，Ｏ点的固定铰链约束反力以正交的Ｆ_Ox、Ｆ_Oy 表示。各力组成平面任意力系，根据平衡条件列出平衡方程如下

    ∑Ｆ_x=0                         Ｆ_Ox－Ｆ_NB  = 0                         （1）

    ∑Ｆ_y=0                         Ｆ_Oy－Ｆ_Q = 0                          （2）

    ∑Ｍo（F）= 0                   Ｆ_NBＯＢ－Ｍ=0                        （3）

解方程得                         Ｆ_Ox=Ｆ_NB  = 0.133 kN

                                  Ｆ_Oy =Ｆ_Q= 0.4kN

                                 Ｍ =Ｆ_NB×400=53.2N·m

拓展训练

1、除了发动机曲柄滑块机构，找出汽车上另外一些连杆机构传动的应用。

2、通过拆装曲轴飞轮组，观察曲柄连杆机构各构件的相互装配关系，该机构如何克服死点位置？
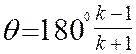