【学习目标】

1.理解函数的单调性与奇偶性的概念。

2.会借助于函数图像讨论函数的单调性。

3.理解具有奇偶性的函数的图像特征，会判断简单函数的奇偶性。

4.通过利用函数图像研究函数性质，培养学生的观察能力。

5.通过函数奇偶性的判断，培养学生的数据处理能力。

6.理解函数的最大(小)值定义及求法.

【学习重点】

1.单调性：

（1）概念：函数值随着自变量的增大而增大（或减小）的性质叫做函数的单调性。

（2）类型：

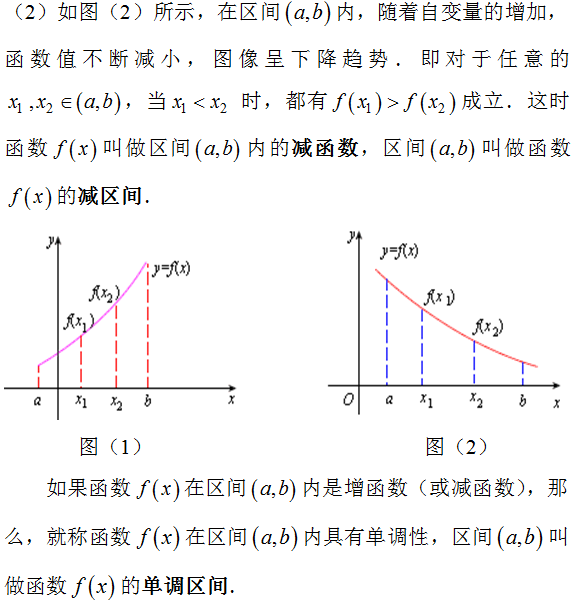
（3）几何特征：在自变量取值区间上，顺着x轴的正方向，若函数的图像上升，则函数为增函数；若图像下降则函数为减函数。

（4）判定方法：判定函数的单调性有两种方法：借助于函数的图像或根据单调性的定义来判定。

2.奇偶性：

（1）概念：

（2）判断：

3.函数的最大值与最小值

最大值  一般地,设函数y= f（x）的定义域为D

         如果对于任意x∈D都有f（x）≤f（x₀），则称f（x₀）      为函数y= f（x）的最大值 ,记作y_max= f（x₀）

最小值 如果对于任意的x∈D都有f（x）≥f（x₀）则称f（x₀）    为函数y=f（x）的最小值

　　　　记作y_min =f（x₀）

如　　  函数y＝x²－2有y_min =f（０）＝－2

  函数y＝－x²－１有y_max =f（０）＝1

最大值与最小值统称为函数的最值。

【课程视频】

【课后练习】