【学习目标】

1.理解实数的大小与比较, 会用数轴上的点表示实数并比较大小.

2.理解不等式的性质, 并学会应用性质比较大小.
3.理解集合的概念, 掌握集合的表示方法, 并学会表示不等式的解集.
4.理解区间的概念, 掌握区间与集合表示的相互转换.

【学习重点】

一、实数的大小比较

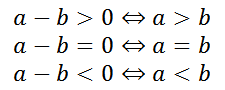
可以通过作差比较两实数的大小.

二、.不等式的基本性质

三、集合

1.集合的概念：

将某些确定的对象看成一个整体就构成一个集合（简称集）。

组成集合的对象叫做这个集合的元素。

2.集合的类型：

数集、点集、解集、有限集、无限集、空集。

3.元素的性质：

确定性；无序性；互异性。

4.元素与集合的关系：

元素a是集合A的元素，记作a∈A，读作a属于A。

元素a不是集合A的元素，记作a∉A，读作a不属于A。

5.集合的表示法：

列举法：把集合的元素一一列举出来，写在大括号内，元素之间用逗号隔开。

描述法：在花括号中画一条竖线,竖线的左侧写上集合的代表元素x，并标出元素的取值范围，竖线的右边侧写出元素所具有的特征性质。

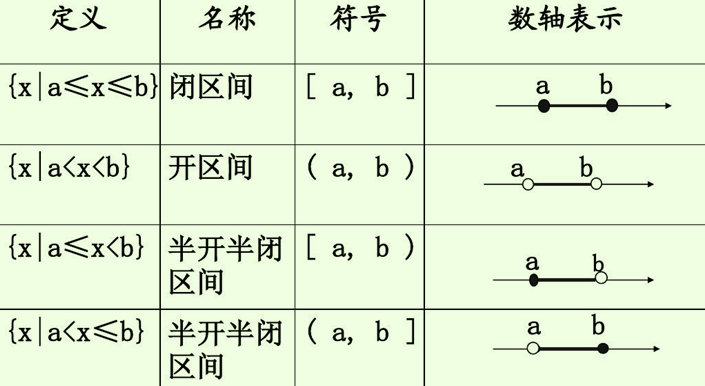
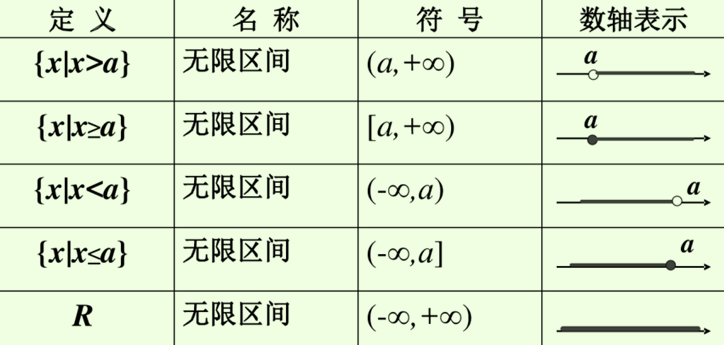
四、区间

概念：一般地，由数轴上两点间的一切实数所组成的集合叫做区间。其中，这两个点叫做区间端点。不含端点的区间叫做开区间。含有两个端点的区间叫做闭区间。只含左端点的区间叫做右半开区间。只含右端点的区间叫做左半开区间。

【课程视频】

【课后练习】