3.1 聚合物分子量及其分布的表征

高分子是由小分子单体聚合而成的，单体的力学强度和韧性都很低，没有使用价值。然而，把单体聚合成高分子材料之后，其力学强度却可以和木材、水泥甚至钢铁相比。分子量上的差别表现在材料性质上的巨大飞跃，这是一个从量变到质变的过程。高分子的许多优良性能都与其分子量相关。并且，这些性能还随着分子量的增大而提高。然而，当分子量增大到一定数值后，上述各种性能提高的速率将减慢，最后趋向于某一极限值。 

分子量对聚合物的主要影响：黏度、力学性能、加工性能、成本等，例如：除力学性能外，聚合物的熔体粘度也随着分子量的增大而增加，当分子量增达到某一程度时，其熔融状态的流动性就很差，将给成型加工造成困难，生产成本增加。

课程思政：结合我校无醛大豆胶黏剂产业化应用案例，介绍高分子材料工程实践关于综合考虑并均衡相关各方矛盾与冲突的思想与必要性。

因此，兼顾到力学性能、加工性能和高分子溶液熔体特性等各方面的要求，需要对聚合物的分子量加以控制。当然，不同的材料、不同的用途和不同的加工方法对分子量的要求是不同的，因此，必须研究聚合条件对产物分子量的影响，以及分子量对材料的加工和使用性能的影响。这些都要求对聚合物分子量进行正确的表征与测量。

然而，测定聚合物的分子量，比低分子物质要困难得多，这不仅是由于其分子量比低分子大几个数量级，而且还由于其分子量的多分散性所致，即聚合物分子的分子量不同。对着众多分散性的描述，最为直观的方法是利用某种形式的分子量分布函数或分布曲线。多数情况还是直接测定其平均分子量。

平均分子量有不同的统计方法，因而具有各种不同的数值。常用的平均分子量有如下四种：

1)  数均分子量：按照聚合物的分子数目 （n_i）进行统计平均。

2)  重均分子量：按照聚合物的质量（W_i）进行统计平均。

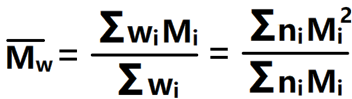
3)  Z均分子量：按照聚合物的Z量 （Z=n_iW_i）进行统计平均。

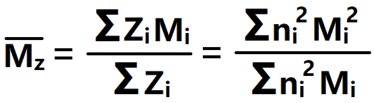
4)  黏均分子量：由稀溶液粘度法测得，无明确物理意义（式中：a是常数，取值为0.5-0.8）。 

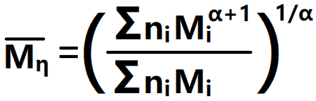
在上述四种平均分子量中，以数均分子量和质均分之量最为常用，而Z均分子量和粘均分子量因物理意义不明确，应用较少。

通常：

对于聚合物分子量的分布有多种表达方法，最简便和最常用的方法是求分布系数D，它等于质均分子量和数均分子量的比值：

      分布系数D= 质均分子量 / 数均分子量

 因为数均分子量 < 质均分子量，所以分布指数D>1。D越大说明聚合物分子量分布越宽，分子量分布越不均一。