1. 计算顶点在格点上的多边形面积（如图2）

（1）分割图形：将多边形分割为长方形和三角形，分别计算面积。

（2）数格点：用a表示多边形内部的格点数，b表示多边形边界上的格点数，则多边形的面积精确值为

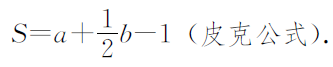
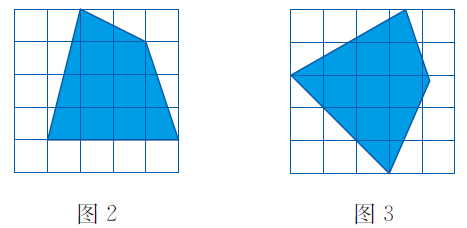
2. 近似计算顶点不全在格点上多边形的面积（如图3）。

数方格：用a表示多边形内部完整的方格数，b表示不完整的方格数，则多边形面积的近似值为

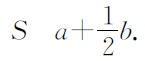
此时数格点的方法也只能得到面积的近似值。

3. 按比例尺换算：

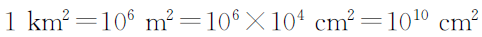
对任意的由封闭曲线围成的平面图形，也可以采用“数方格”或“数格点”的方法近似计算其面积。