统计推论之核心概念
上一节
下一节
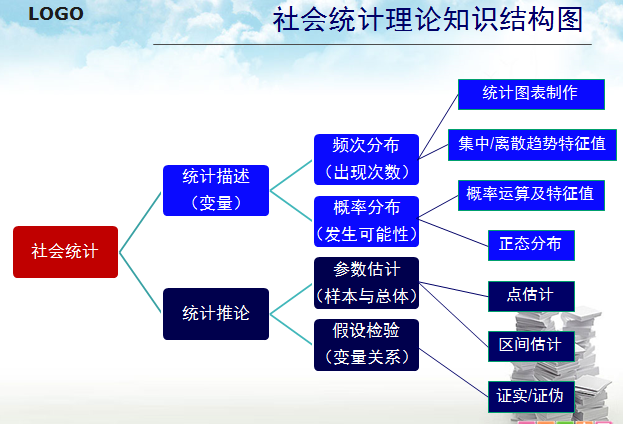

统计推论讲的是总体与样本之间的关系,肯定了样本在一定程度上涵盖了总体的特性,当总体的某种特征值未知时,可以通过样本的统计来对总体特征值加以推断。
样本资料在某种程度上能反映总体的特性,由于社会资料的随机性,即抽样的结果不是唯一的,一次抽样结果不能恰好就等于总体的特性
在总体参数不知道的情况下,抽样结果是否等于总体参数,是不知情的——不确定性——推论
二、总体、个体、样本
总体——依据我们研究目的而确定的观察单位某种变量值的集合。
个体——总体中每一个对象视为个体。
样本——从总体中按方式抽出的一部分个体;样本是由个体组成的,其中包含的个体数目n称为样本大小或样本容量。
举例:研究某厂生产的灯泡的使用寿命,该厂生产的所有灯泡的使用寿命为总体,每个灯泡的使用寿命为一个个体,从所有抽取部分灯泡的寿命进行检测,被抽取的灯泡的寿命即为样本。
三、简单随机样本——满足统计推论的基本条件
如果所抽取的样本不但是随机变量,而且相互独立,遵从同一分布,那么这样的样本就称作简单随机样本
获取方法——
无限总体中的随机抽样、有限总体中的重复抽样(回置抽取)
随机样本具有两重性,
抽样之前属于一组随机变量(e1,e2,e3,…,en),
抽样之后则为一组具体、确定的数值(X1,X2,X3,……Xn)
四、统计量与观测值
随机变量e1,e2,e3,……,en的函数f(e1,e2,e3,…,en)叫作统计量
根据随机变量e1,e2,e3的观测值X1,X2,X3,计算得到的一切统计数字特征,可以看做是相应统计量的观测值;
统计量是理论值,存在多种可能,观测值是确定值;


