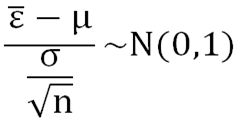第四节 大数定理

大量随机现象平均结果的稳定性的一系列定理，称为大数定理

大数定理是在一般条件下，包括偶然性因素在内的大量个别原因和个别条件所共同作用的结果，而这种最后结果摆脱了偶然性的影响

大数定理——

在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。通俗地说，这个定理就是，在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。

我们可以用特征值对变量分布的特征作概括、简化的研究（均值，方差）；反过来，如果变量的特征值已经知道，对分布也可以作出粗略的估计；

变量取值的概率分布    特征值（均值、方差）

切贝谢夫不等式

通过随机变量的数学期望和方差对变量在区间[E(e)-a,E(e)+ a]的概率所作最保守的估计；

因为均值与方差已经凝聚了变量分布的基本特征和主要信息了

如果随机变量e，有数学期望E(e)和方差D(e),则不论e的分布如何，对于任何正数a，都可以断言，e和E(e)的绝对离差

大于等于a的概率，不超过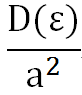

切贝谢夫不等式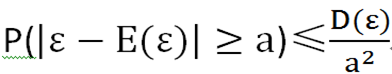  或者

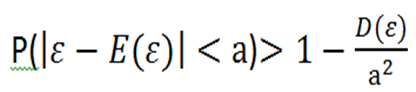
例题：

某地进行了电话费用的情况调查。电话费用的分布不清楚。但知道平均电话费用为80元，标准差为10元。问60-100元之间的概率是多少？

E(ε)=80元 D(ε)=102  

依据切贝谢夫不等式  变量取值范围在60-100之间，a可取20元

P(|ε-80|≤20)>1 - (D(ε))/a2 =1- (10)2/(20)2 =0.75

因此，电话费在60-100元之间的概率将大于0.75

中心极限定理——大量现象在分布上呈现的稳定特征

e1，e2，e3，…，en为独立同分布的随机变量，不管其分布如何，只要E(ei)=m,D(ei)=     (i=1,2,3,…)存在，

(1)只要n足够大，

(2)只要n足够大,

(3)只要n足够大，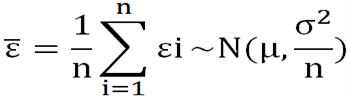

（4）只要n足够大，